На рисунке 2.1, б приведен фазовый портрет системы (2.9) при tx >> ty. Видно, что траектории во всех точках, кроме лежащих на изоклине горизонталей, практически вертикальны, поскольку Dy >> Dx. Поэтому изображающая точка очень быстро, за время ty, попадает на изоклину горизонталей и затем медленно движется к стационарному состоянию согласно (2.10). Формально траектория плавная, но на ней имеется очень крутой поворот в точке(x1 , y2). Уравнение (2.10) этот крутой поворот не описывает, с чем и связано нарушение аналитических свойств решения полной системы (2.9).

Начальное значение переменной y1 в уравнении (2.10) не фигурирует, важно лишь значение x1 . Любое другое значение y, лежащее на вертикали x=x1 приводит к тому же результату. Иными словами, редуцированная система забывает о начальном значении y.
Таким образом редуцированная система правильно описывает процесс на
ограниченном, но наиболее важном для данной задачи, временном интервале.
Информационные аспекты редукции (и теоремы Тихонова) в следующем. При редукции сложной системы количество информации сокращается, сохраняется только ценная информация, а не ценная забывается.

Мы остановились на этом примере столь детально, поскольку редукция сложных систем играет очень важную роль при описании и исследовании процессов самоорганизации.
Как упоминалось, редукция основана на временной иерархии. Возникает вопрос: в каких случаях она имеет место и почему. В неживой природе она имеет место далеко не всегда. Так, например, при горении водорода образуется много промежуточных продуктов и времена их взаимопревращений примерно одного порядка. В процессах самоорганизации в живой природе, напротив, временная организация наблюдается практически всегда. Тому есть причины. Дело в том, что задачи моделирования и самоуправления во многом сходны и временная иерархия необходима и для того и для другого.
Отсюда следует на первый взгляд парадоксальный вывод: построение математических моделей живых самоорганизующихся систем — задача более простая, чем моделирование процессов в неживой природе, хотя и последнее интересно и важно. Возможно, именно с этим связаны успехи синергетики в биологии, экологии и социальных науках.
Стационарные состояния динамической системы могут быть разного типа. Их классификацию удобно привести на примере системы (2.9),

1. Устойчивый узел — так называется стационарное состояние в случае, если траектории упираются в точку, то есть приближаются к ней апериодически. При этом в линейном приближении вблизи точки все числа Ляпунова вещественны и отрицательны.
2. Устойчивый фокус — в этом случае траектории имеют вид свертывающихся спиралей и изображающая точка приближается к стационару, совершая затухающие колебания. При этом числа Ляпунова комплексны; реальная часть их отрицательна, а мнимая равна частоте колебаний.
3. Центр — в этом случае траектория представляет собой замкнутые кривые. Числа Ляпунова при этом чисто мнимые. В системе происходят незатухающие колебания амплитуда которых зависит от начальных условий (но не от параметров системы). Частота (т.е. мнимая часть числа Ляпунова) напротив, определяется внутренними свойствами системы.
   Состояние «центр» нейтрально, то есть ни устойчиво, ни неустойчиво.
4. Неустойчивый фокус — в этом случае траектории — раскручивающиеся спирали. Числа Ляпунова определенные в линейном приближении комплексны, и реальная часть их положительна.
   В реальных системах, как правило, раскручивание спирали ограничивается нелинейными членами. Тогда раскручивающаяся спираль навивается на замкнутую траекторию изнутри. Другие траектории, стремящиеся к неустойчивому фокусу из одаленных областей фазового пространства, навиваются на замкнутую траекторию снаружи. Эта замкнутая траектория называется предельным циклом (или циклом Пуанкаре). Движение точки по предельному циклу описывает периодический процесс. В отличие от центра, в данном случае амплитуда и период определенный внутренними свойствами системы и не зависит от начальных условий.
5. Седло — неустойчивое состояние в котором, хотя бы одно из чисел Ляпунова положительно. На фазовом портрете системы типа 2.2 через седло проходит только две особых линии. Одна из них такова, что изображающие точки движутся по ней к седлу и упираются в него. Эта линия называется сепаратрисой. Другая такова, что точки движутся от седла в разные стороны. Остальные траектории «обтекают» седло (в ту или иную сторону) и не попадают в него. Примером может служить движение шарика в потенциальном поле имеющем форму седла ( или перевала) — отсюда и происхождение названия — седло.

Точки типы «седла» с необходимостью возникают в бистабильных системах, где имеется два разных центра притяжения (типа устойчивого узла или фокуса). Линия, проходящая через седло разделяет области притяжения устойчивых точек — отсюда ясно и ее название — сепаритриса, то есть разделяющая.
Конкретные примеры таких систем мы приведем ниже. Отметим, что в гамильтоновых системах могут существовать только особые точки типа седла и центра. Другие стационарные состояния в них невозможны.
Продемонстрируем метод построения фазового портрета на ряде конкретных примеров.
Рассмотрим бистабильную колебательную систему вида:

(2.11)

Она описывает движение шарика массы m в потенциальном поле V(x) при наличии трения (коэфициент трения — g)

(2.12)

Первый член левой части (2.11) — сила инерции, второй — сила трения, пропорциональная скорости.
Потенциал V(x) представлен на рисунке 2.2.
Видно, что имеются две лунки, в которых может находиться шарик и барьер между ними. Если кинетическая энергия шарика достаточно велика, то он может колебаться между лунками.
Для построения фазового портрета системы (2.11) удобно её представить в виде двух уравнений для координаты x и импульса р.

(2.13)

где обозначено:

Фазовый портрет системы (2.13) приведен на рисунке 2.3.
Пересечение изоклин — стационарные состояния — расположены в точках: x=1 , x=-1 и x=0. Средняя из них — седловая. Таким образом, система бистабильна и выбор конечного состояния зависит от начального положения изображающей точки. Траектории — спирали. Сепаратрисы, будучи сами траекториями, тоже имеют спиральную форму, они изображены на рисунке жирными линиями. Слои между сепаратрисами — области притяжения устойчивых состояний. Толщина слоев зависит от коэффициента трения g, спирали сгущаются при уменьшении последнего.

Уравнение (2.11) качественно описывает игру в «орлянку», то есть вращение подброшенной в воздух монеты и последующее падение её. Два стационарных состояния соответствуют «орлу» или «решке». Трение монеты о воздух очень мало и сепаратрисы плотно заполняют фазовое пространство. Малое, но конечное изменение начального условия или малое внешнее воздействие может перебросить точку в соседний слой, что приводит к изменению выбора системой конечного состояния, то есть к генерации информации.

Физический смысл описанного прост: если шарик имеет вначале достаточно большую кинетическую энергию, то до остановки он совершит так много колебаний, что предугадать результат очень сложно. Если начальные условия заданы на сепаратрисе, то это вообще невозможно.
В отсутствии трения (g=0), спирали замыкаются и устойчивые фокусы превращаются в центры, то есть нейтральные состояния (числа Ляпунова при этом чисто мнимые). Уравнения (2.13) при этом описывают незатухающие колебаня. При малых амплитудах — колебания вокруг стационарной точки (либо x = +1, либо x=-1). При больших амплитудах — это колебания вокруг обеих точек.
Положение изображающей точки на плоскости (x,p) определяет как координату(x), так и импульс (р). Угол между линией, направленной из начала координат к изображающей точке, и абсциссой представляет собой фазу колебаний. Отсюда происходит название — фазовая плоскость.
В отсутствии трения (g=0) решение уравнения ((2.11) существенно упрощается. Тому есть причина, причем фундаментальная — закон сохранения энергии. Полная энергия, то есть сумма кинетической и потенциальной энерги

(2. 14)

не изменяется со временем. Величина Н называется гамильтонианом, а соответствуюшие системы — гамильтоновыми. Используется и другое название — консервативные системы. Этим подчеркивается, что некая величина, в данном случае энергия, сохраняется.
В общем случае, при наличии трения энергия (2.14) не сохраняется, точнее, она рассеивается, диссипирует, переходит в тепло. Такие системы называются диссипативными, происхождение термина очевидно.
При очень сильной диссипации ( ) в уравнении (2.11) можно пренебречь силой инерции и представить его в виде:

(2.15)

Оно описывает движение легкого шарика в потенциальном поле V(x) в очень вязкой жидкости. Оно же описывает простейшую запоминающую ячейку — триггерный элемент.
В настоящее время термин «диссипативные системы» очень популярен поэтому его уместно обсудить более детально.
Существующая в теории динамических систем терминология заимствована из механики, где такие понятия как энергия, импульс, диссипация имеют четкий смысл. Там же, в механике, квантовой механике, теории поля и т. п. ( то есть в «фундаментальных» науках) рассматриваются преимущественно гамильтоновы системы. Тому есть причины:
Во-первых, закон сохранения энергии действительно фундаментальный. Он действительно соблюдается в каждом отдельном акте взаимодействия элементарных частиц и физических полей. В более сложных процессах происходит диссипация энергии и эту проблему мы рассмотрим позже.
Во-вторых, методы исследования гамильтоновых систем детально разработаны.

В реальной жизни, и в частности, в процессах, связанных с информацией, приходится иметь дело с диссипативными системами. Таким образом, область применимости гамильтоновых систем в реальной жизни крайне узка.
Мы остановились на этом вопросе, поскольку до сих пор не прекращаются попытки построить «фундаментальную биологию» или «фундаментальную информатику» по образу и подобию гамильтоновой механики. Из изложенного следует, что попытки уложить реальную жизнь в прокрустово ложе гамильтоновых систем обречены на неудачу.
Рассмотрим фазовый портрет еще одной системы, имеющей отношение к информации и, в частности, к процессу генерации информации в биологических системах (возникновению единого генетического кода) [7,8,14]. Система состоит из двух уравнений

Обсудим сперва свойства системы (2.16) в симметричном случае. когда а1 =а2=а. Фазовый портрет её представлен на рисунке 2.4.
Изоклины вертикалей (Du1 = 0) определяются из условия F1( u1, u2 ) = u1 — u1 u2 — а u12 = 0 и соответствуют линиям u1 = 0 и u2 = 1 — а u1 . Изоклины горизонталей (Du2 = 0) определяются из условия u2 — u1 u2 — а u22 = 0 и соответствуют линиям u2 = 0 и u1= 1 — аu2.
(см.рис.2.4). Система имеет четыре стационарных состояния. Первое расположено при u1 = u2 = 0 и неустойчиво. Оба числа Ляпунова положительны и равны l1,2 =+1. Такая точка называется неустойчивым узлом.

Второе расположено на биссектрисе u1 = u2 = (1 + а)-1 и тоже неустойчиво (типа седла). Имеются два устойчивых состояния (типа узла): при u1 = 1/а (u2 = 0) и при u2 = 1/а ( u1 =0); в них оба числа Ляпунова отрицательны. Вся плоскость разделяется сепаратрисой на две области; в каждой из них траектории стремятся к соответствующему устойчивому состоянию. В нашем случае в силу симметрии системы она совпадает с биссектрисой.
Эта модель позволяет проследить процесс рецепции информации и возникновение (генерацию) ее. Так, если в силу внешних причин начальные условия не симметричны, то система приходит к определенному стационарному состоянию — это рецепция информации.
Если заранее выбор не предопределен, то есть начальные условия симметричны и заданы на сепаратрисе, то система сама, по воле случая, выбирает одно из стационарных состояний — это генерация информации. Ниже мы вернемся к этой системе и обсудим ее более детально.
В случае, когда коэффициенты а1 и а2 не одинаковы (например, 1> а2 >а1 ) симметрия нарушается, но качественные свойства системы сохраняются: имеются две области притяжения, они различны, но сопоставимы. Фазовый портрет представлен на рисунке 2.5.

Мы уже обсуждали вопрос о связи информации и необратимости, имеющий принципиальное значение. В идеально обратимом мире информация не может возникнуть, поскольку любой выбор не может быть запомнен, ( запоминание возможно лишь в диссипативных системах). Поэтому необратимость в нашем мире играет существенную конструктивную роль. Однако, в фундаментальных законах классической и квантовой физики время входит обратимо, так, что замена скоростей частиц на обратные эквивалентна повороту стрелы времени (т.е. замене t ® — t). Иными словами, в гамильтоновых системах явление необратимости не может иметь места.

В науке этот вопрос возник в очень острой форме на рубеже XIX и XX столетий. История вопроса поучительна и трагична. Людвиг Больцман был первым, кто попытался решить эту проблему. Он поставил цель: «вывести» законы термодинамики из уравнений Ньютона. Для этого рассмотрел систему из многих шаров, движущихся по ограниченной плоскости (биллиард Больцмана) и упруго соударяющихся друг с другом. Проведя, казалось бы, естественное усреднение, Больцман получил результаты, носящие его имя:
(1) закон возрастания энтропии (так называемая Н-теорема Больцмана),
(2) соотношение между энтропией и вероятностью:

где k = 1.38*10-16 эрг/град. — постоянная Больцмана и W — вероятность застать систему в определенном состоянии, где скорости и координаты шаров имеют определенное значение,
Эти результаты вошли в «золотой фонд» современной физики. Вместе с тем корректность расчетов Больцмана вызвала сомнение. Друг и постоянный оппонент Больцмана — математик Цермелло — возразил: изначальные уравнения симметричны во времени, а результат (возрастание энтропии) явно не симметричен. Такого не может быть, если все промежуточные вычисления математически корректны; следовательно, где-то допущена ошибка.
Больцман не смог ответить и застрелился.

Следующим был замечательный физик Эренфест. Он сформулировал проблему максимально четко, но ответа дать не смог и застрелился.
Идея ответа была найдена молодым физиком Н.С. Крыловым в 1948 г [15]; он вскоре умер.
В нашем изложении эта история выглядит трагикомически. В действительности решение покончить с жизнью человек принимает в состоянии эмоциональной неуравновешенности и неустойчивости. Искать непосредственную причину такого выбора бессмысленно. Важен другой вопрос: какие обстоятельства привели человека в неустойчивое состояние?

Что касается Людвига Больцмана ответ ясен. В научной среде его результаты встретили серьезное сопротивление. Попросту. он был подвергнут травле. В этом принимали участие не только друг Больцмана Цермелло (со стороны друзей это, как раз, часто случается), но и крупные, казалось бы объективные, ученые. Так, Пуанкаре «открыто рекомендовал не изучать труды Больцмана. поскольку они противоречили его, Пуанкаре, выводам» (цитируется по [9]). Удивительно и поучительно почему Пуанкаре, один из основоположников теории устойчивости, не смог понять результатов Больцмана и связать их с неустойчивостью (что впоследствии сделал Н.С. Крылов). Дело в том. что для Пуанкаре (как и для многих представителей французской школы математиков) принцип детерминизма был святыней. Он не мог даже допустить мысли о возможной ревизии понятий «причина» и «следствие». Этот эпизод — пример тому, как даже великий ум, будучи в плену сложившихся представлений, не может оценить значение своих же собственных результатов.

Что касается Эренфеста, то здесь дело в другом. Главной причиной самоубийства, повидимому, послужили трагические обстоятельства семейного плана. Хотя. и в этом случае сознание неспособности решить поставленную задачу, возможно, играло важную роль.
Что касается Н.С. Крылова, то его ранняя кончина казалась естественной: слабое здоровье, усугубленное тяготами военных лет. Однако. и его научный путь не был усеян розами. Коллеги Н.С. Крылова отнеслись к его идее с настороженностью и поставили вопрос: Откуда берутся малые случайные возмущения? По отношению к неустойчивым процессам такой вопрос, как мы теперь знаем, не корректен и лишен смысла, однако, тогда он казался естественным. Ими же (коллегами) был подсказан ответ: случайные возмущения следуют из соотношения неопределенности (т.е. из квантовой механики). Крылов, под давление общественности. согласился с этим ответом (хотя. внутренне, повидимому, был не удовлетворен им). Вскоре выяснилось. что такой ответ не верен. поскольку в квантовой механике проблема необратимости времени стоит не менее остро. чем в классической (подробнее мы обсудим её позже). В результате в памяти физиков Н.С. Крылов остался, как человек, который пытался проблему необратимости в классике решить за счет квантовой механики, в чем был не прав. Повлияли-ли научные дискуссии на судьбу Н.С. Крылова — судить не будем, важно. что его идеи не были забыты.
Далее события развивались менее драматично. В работах Колмогорова [16], Синая и Амосова [17,18,19] идеи Крылова были оформлены математически корректно. Сейчас результаты известны как теорема Синая . Изложим суть дела.
В механике обратимость во времени означает следующее.

Пусть тело (например, шар в биллиарде Больцмана) в начальный момент (t=0) имеет координаты x0 и скорость v0 и далее движется в соответствии с законами механики. Если в момент времени t1 изменить знак скорости, то по прошествии того же времени t1 тело вернется в точку x0 и будет иметь скорость, равную — v0. (далее такой процесс будем называть обратимым). Этот результат связан с инвариантностью уравнений по отношению к инверсии времени (о чем уже шла речь выше). Это же свойство обеспечивает сохранение энергии в классической механике.
Если такую процедуру провести со всеми шарами биллиарда Больцмана, то все они вернутся на исходные места (хотя и будут иметь противоположные скорости).
В частности, если вначале (t=0) все шары были сконцентрированы в малой части доступного пространства, то после описанной процедуры они должны собраться там же.
Этот результат означает, что энтропии начального и конечного состояний должны быть одинаковы и, следовательно, энтропия в динамических процессах не может возрастать (что и составляло суть возражений Цермелло).
Ясно, с другой стороны, что молекулы газа ведут себя иначе и никогда не собираются обратно. При расширении газа энтропия возрастает и не может затем уменьшиться, даже если изменить знаки скоростей.

В чем здесь дело? Утверждать, что уравнения движения механики не применимы к шарам нельзя; траектории шаров должны им подчиняться (и реально подчиняются).
Для решения парадокса было привлечено понятие устойчивости; в этом и заключалась идея Крылова.
В задаче Больцмана, следует задаться вопросом: устойчиво ли движение шаров в биллиарде? Если оно устойчиво, то Цермелло и Пуанкаре правы , и результаты Больцмана не корректны. Если оно неустойчиво, то это обстоятельство и является «причиной» необратимости процесса. Тогда строгие математические расчеты механических траекторий не могут описать реальный процесс; необходим другой подход, другой метод расчета, который позволил бы получить устойчивые результаты. Метод усреднения, который использовал Больцман, позволяет получить устойчивые результаты для средних величин и потому является конструктивным и в этом смысле корректным. Он вполне оправдан в случае, когда траектории шаров неустойчивы.

Рассмотрим, устойчивы ли траектории шаров в биллиарде Больцмана. Движения шаров между соударениями нейтральны, поэтому неустойчивость может возникнуть лишь при соударении шаров. Задачу можно упростить и рассмотреть многократное отражение материальной точки от выпуклой поверхности кривизны R (R=2r, где r — радиус шара). Для этого представим, что точка находится в ограниченном пространстве, в котором хотя бы одна из отражающих поверхностей выпукла (схема процесса приведена на рис. 2.6). Эта задача была поставлена и решена Л.Г. Синаем, и рисунок 2.6 носит название «биллиард Синая».
Не будем детально излагать теорему Синая, лишь на примере поясним суть дела. Рассмотрим угловые отклонения возмущенной траектории от исходной до и после соударения.
Траектория шара представляет собой ломаную линию. Точки излома соответствуют отражениям шара от стенки, плоской или выпуклой. В обоих случаях угол падения bi равен углу отражения.
Зададимся вопросом: устойчиво ли это движение и каковы числа Ляпунова траектории . Для этой цели проанализируем угловые отклонения. Рассмотрим два прямолинейных участка до и после отражения от выпуклой стенки (i-ый и i+1-ый).
Сравним две траектории, одна из которых на i-ом участке отклонена от другой на малый угол ai <<1, и вычислим угол отклонения ai+1 на следующем участке. Он равен:

(2.18)

где: li -длина пробега.
Вывод рекуррентного соотношения (2.18) легко провести, используя рис. 2.6 и сведения из школьного курса геометрии.
Из (2.18) следует, что угловое отклонение возрастает при каждом отражении от выпуклой стенки. Используя соотношение (2.18), можно угловое отклонение am после m-ого соударения выразить через начальное угловое отклонение a0

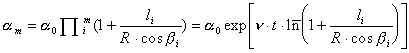(2.19)

где: a0 -начальное отклонение (при t=0); n- число соударений за единицу времени ( m=nt); черта над логарифмом означает усреднение по числу соударений Из (2.19) следует, что движение шара в биллиарде Синая неустойчиво, числа Ляпунова положительны и равны

(2.20)

Этот вывод справедлив по отношению к любой траектории, в которой имеет место соударение с выпуклой поверхностью. Более того, этот вывод сохраняется и для обратного процесса, поэтому систему можно считать глобально неустойчивой.
Рассмотрим структуру фазового пространства системы. Имеется четыре динамических переменных: две координаты x и y и два импульса px и py . Закон сохранения энергии накладывает ограничение:

(2.21)

где p0 — абсолютная величина начального импульса. Поэтому изображающая точка движется в трехмерном пространстве, включающем координатную плоскость и, например, импульс px .
Стационарные состояния располагаются на плоскости (x,y), px =0, py =0 (и, следовательно, p0 =0) и соответствуют исходно покоящемуся шару. При ненулевом значении p0 стационарные состояния недостижимы, так что изображающая точка движется в слое трехмерного пространства, ограниченном значениями px =±p0 . При отражении от плоской границы «с» импульс px сохраняется, при отражениях от «а» и «b» меняется его знак, но не величина. При отражении от выпуклой поверхности «d» изменяется величина px . Проекция траектории на плоскость (x,y) представляется ломаной линией, равномерно заполняющей все координатное пространство. Проекция траектории на ось px представляет собой скачкообразный дрейф, также равномерно заполняющий весь доступный интервал (-p0,+p0).

Рассмотрим ансамбль аналогичных систем, в которых начальные условия отличаются, но слабо. В фазовом пространстве он представляется группой изображающих точек, которые в начале находятся в малой области e ( e — мера различия начальных условий). Окружим область всюду выпуклой поверхностью (как это показано на рис 2.7а). С течением времени в силу глобальной неустойчивости точки будут разбегаться друг от друга и в конце концов равномерно и случайно заполнят все доступное пространство. Выберем промежуточный момент времени и снова окружим все точки всюду выпуклой поверхностью. Объм окруженной области Г(t) будет больше начального Г(0) и с течением времени будет возрастать, пока не охватит все пространство. Величина S , равная:

/Г0

(2.22)

называется энтропией Синая. (Здесь: Г0 — элементарная ячейка фазового пространства, в классической физике эта величина условна, в квантовой механике она ограничена соотношением неопределенности и равна Г0 = h3n , где h — постоянная Планка и n — число частиц) Рост энтропии связан просто с увеличением фазового объема Г(t), обусловленного глобальной неустойчивостью.

Системы с такими свойствами называются эргодическими. Свойство эргодичности лежит в основе современной термодинамики. Ранее оно вводилось постулативно и называлось эргодической гипотезой (или гипотезой о микрохаосе ), которую теперь можно считать не гипотезой, а следствием теоремы Синая.
В случае, когда выпуклая поверхность заменена плоской (т.е. R®Ґ), число Ляпунова согласно (6) равно нулю, то есть система устойчива. Абсолютная величина импульса px сохраняется при любом соударении. Изображающая точка движется только в двух плоскостях: px = +px(0) и px =-px(0), и перескакивает с одной на другую при отражениях от стенок «а» и»b». Плоскость (x,y) заполняется траекторией равномерно, но не хаотично.
Ансамбль изображающих точек не расплывается, так что энтропия Синая со временем не возрастает. Такая система не является эргодической.
В связи с этим уместно упомянуть еще об одном парадоксе классической механики.
Согласно теореме Лиувилля объем области, занятой ансамблем в динамических гамильтоновых системах не может изменяться со временем. Это утверждение справедливо по отношению к устойчивым системам, где изображающие точки не разбегаются.

При глобальной неустойчивости возникает вопрос , что понимать под «объемом области». Например, можно окружить ансамбль точек не всюду выпуклой поверхностью так, что объем внутренней области будет сохраняться даже в случае разбегания точек, так, как это показано на рис. 2.7б При этом теорема Лиувилля формально соблюдается, однако вычислить вероятность нахождения системы в данной точке фазового пространства невозможно. При построении лиувиллевского объема фазовое пространство оказывается сильно расслоенным, так, что толщина слоёв меньше. чем обратный гугол Введение всюду выпуклой поверхности равносильно сглаживанию, то есть замене изрезанной функции её средним значением. При этом вероятности нахождения системы в любой точке, окруженной выпуклой оболочкой, одинаковы. Это позволяет перейти от динамического описания эргодических систем к статистическому.

Таким образом, подход Синая можно рассматривать как пример конструктивного использования понятия «обратный гугол».
Можно показать, что в случае термодинамически равновесного идеального газа (содержащего много частиц (т.е. «шаров»)) энтропия Синая совпадает с энтропией Больцмана, то есть с физической энтропией. Действительно, термодинамически равновесное состояние представляет собой совокупность микросостояний, каждое из которых неустойчиво и через короткое время заменяется другим. При этом величина Г(t) в (2.22) равна Гmax т.е. максимально доступному фазовому объему. Вероятность обнаружить систему в каком либо одном микросостоянии (т.е. величина W в (2.17)) равна отношению: Гmax / Г0 . Откуда следует, что выражения (2.17) и (2.22) в этом случае совпадают.
С механической точки зрения равновесное макросостояние вообще не является состоянием, и описывать его в терминах механики бессмысленно. Однако, средние характеристики его со временем не изменяются, то есть стационарны и устойчивы. К таковым относятся: средняя кинетическая энергия частиц (температура), средний импульс, передаваемый в единицу времени единице поверхности при соударениях со стенкой (давление) и усредненное по ансамблю распределение частиц по энергиям. Это распределение было получено Больцманом. Вывод его можно найти во многих руководствах (см. например, [20]).
Энтропия в свете изложенного представляет собой не более чем удобную, хотя и условную, меру вероятности. В принципе можно было бы вообще обойтись без этого понятия и оперировать вероятностями. Однако это неудобно, поскольку вероятности, как правило, очень малы (меньше чем обратный «гугол» , а энтропия (в силу логарифмической зависимости ) выражается разумным числом). Утверждение о том, что энтропия может только увеличиваться, означает, что в глобально неустойчивых процессах изображающие точки разбегаются друг от друга независимо от того, рассматриваем ли мы процесс в прямом или обратном направлении времени.
В заключение уместно сделать ряд замечаний.

i) Эргодичность является следствием глобальной неустойчивости, возникающей при взаимодействии частиц, но не связана с числом частиц.
Действительно, в биллиарде Синая имеется только одна частица, и ее траектория с течением времени равномерно заполняет все доступное фазовое пространство (т.е. система эргодична). В биллиарде Больцмана достаточно нескольких шаров для того, чтобы (в силу неустойчивости их соударений) заполнить все доступное фазовое пространство. При этом распределение их по энергиям подчиняется закону Больцмана.
С другой стороны, в системах, содержащих много частиц, но движущихся устойчиво, эргодичность не имеет места. Примером может служить солнечная система, в которой имеются десятки тел (планет, спутников и т.д.), поведение которых отнюдь не хаотично.
Мы остановились на этом, поскольку во многих руководствах утверждается, что большое число частиц является необходимым и достаточным условием эргодичности, что в свете изложенного, неверно.

ii) В задачах Больцмана и Синая рассмотрены взаимодействия с так называемым «жестким кором». Принято, что взаимодействие отсутствует, если расстояние между шарами больше двух радиусов шаров. Сближение шаров на расстояние, меньшее удвоенного радиуса, исключается. Такому взаимодействию соответствует потенциал в виде бесконечной стенки на расстоянии двух радиусов. При этом параметр — радиус взаимодействия — имеет четкий смысл. При взаимодействии реальных частиц (атомов и/или молекул) ситуация иная. На малых расстояниях преобладают силы отталкивания, на больших — притяжения. Если потенциал отталкивающих сил U(r) зависит от расстояния r достаточно резко (например, U(r)»1/rn , n >2), то можно ввести «эффективный радиус», и в этом случае результаты Синая сохраняются.
Если же имеет место дальнодействие (то есть потенциал U(r)»1/r), то эффективный радиус становится бесконечным (R®Ґ). Тогда, согласно (6), число l стремится к нулю , то есть движение частиц устойчиво по Ляпунову .

Гравитационные силы являются дальнодействующими, что и объясняет отсутствие хаоса в планетарной системе. Электрические силы также являются дальнодействующими. Поэтому электронно-ионная плазма, строго говоря, не является эргодической системой. Она не является и динамической, поскольку при взаимодействии ионов присутствуют помимо электростатических другие, короткодействующие силы. Поэтому электронно-ионня плазма, практически, не бывает термодинамически равновесной.
Столь подробное рассмотрение сделано с целью подчеркнуть, что термодинамическое равновесие реализуется отнюдь не всегда, а только в глобально неустойчивых системах (или подсистемах).
iii) Устойчивость макроскопических состояний и неустойчивость микроскопических связаны друг с другом. Действительно, условием устойчивости макросостояний является затухание флуктуаций. С другой стороны, любое микросостояние — это флуктуация на фоне макросостояния. Затухание флуктуации означает разрушение микросостояния, что происходит за счет его неустойчивости.

Таким образом, глобальная неустойчивость микросостояний (микроскопический хаос) оказывается необходимым условием макропорядка.
iv) В эргодических системах неустойчивы движения как в прямом, так и в обратном направлении. Это значит, что при обращении знака времени изображающая точка не вернется в исходное положение, а будет «дрейфовать» в фазовом пространстве так, как, если бы знак времени не был изменен. Иными словами, повернуть процесс вспять (или, что то же, изменить знак времени) в глобально неустойчивых системах невозможно.
Это замечание связано с проблемой «стрелы времени». Суть проблемы в следующем. В физике, благодаря успехам теории относительности, принято думать, что пространственные координаты и время в значительной мере равноправны .
С другой стороны, обратимость в пространстве возможна (всегда можно вернуться в исходную точку пространства), но обратимость во времени невозможна (помолодеть нельзя).
Отличие связано со свойством неустойчивости, которое характеризует нарастание отклонений со временем.
v) В рассмотренных системах (задача Больцмана, биллиард Синая) все числа Ляпунова одинаковы (точнее одного порядка). В реальных (в частности, открытых ) системах это не так.
Число показателей Ляпунова равно числу динамических переменных и очень велико. Среди них имеются как положительные, так и отрицательные. Можно преобразовать динамические переменные (ввести так называемое конфигурационное фазовое пространство) так, что в определенной части нового фазового пространства движения будут устойчивы, а в другой части — глобально неустойчивы. Точнее: изображающая точка в многомерном фазовом пространстве всегда движется по одной траектории. Речь идет о том, что проекция этой траектории на первое подпространство устойчива, а проекция на второе — неустойчива. Тогда в первом подпространстве можно (и нужно) использовать законы механики, а во втором — термодинамики.

В макроскопических машинах (например, паровых) разделение фазового пространства на динамическую и статистическую части очевидно: в котле — термодинамика, в механической части (поршень, рычаги и т.п.) — механика. Поэтому вопрос о критериях разделения был не актуален и долгое время вообще не обсуждался. В молекулярных конструкциях (т.е. в биологических «машинах») такое разделение не тривиально и вопрос о критериях актуален [12]. Из изложенного следует, что таким критерием должно служить наличие (или отсутствие) глобальной неустойчивости.

В связи с развитием вычислительной техники появилось новое направление — молекуулярная динамика [21,22]. Цель его — описание поведения ансамбля частиц, исходя из первых принципов, то есть законов Ньютона. Взаимодействие частиц описывается потенциалом (как правило — Ленарда-Джонса). Практически этот метод используется при теоретическом исследовании поведения сложных молекул (в частности биологических). Однако, его можно использовать и для решения вопроса о росте энтропии в биллиарде Больцмана. Для этого достаточно выбрать форму потенциала, соответствующую упругому соударению жестких шаров. Такие расчеты проводились неоднократно [23]. Число частиц в ансамбле выбиралось порядка 100, что, правда, не существенно. Расчеты проводились в ограниченном пространстве с отражающими стенками. Начальные условия задаювались в виде набора координат и импульсов частиц, далее компьютер вычислял их траектории. Результаты таковы:
Траектории шаров не воспроизводимы, то есть имеет место глобальная неустойчивость — хаос. Средние значения, напротив, устойчивы. Обратимость в механическом смысле не имеет места, то есть при обращении знака времени (инверсии скоростей) частицы не движутся по прежним траекториям и не собираются в исходном месте.
Распределение частиц по скоростям устанавливается достаточно быстро (через 10 соударений) и соответствует максвелловскому не зависимо от начальных условий.

Таким образом, основные результаты термодинамики можно получить без использования второго начала, как дополнителного постулата. Понятие энтропия при этом можно ввести, но можно и не вводить и вообще не упоминать о нем.
Разумеется, точность машинного расчета не абсолютна и ошибки заведомо больше, чем обратный гугол. В частности, инверсию скоростей компьютер тоже делает с ошибкой. Однако, именно такой «неточный» расчет приводит к правильным результатам, адекватно описывающим действительность. В этой связи второе начало можно сформулировать в следующем, несколько парадоксальном, виде:
В расчетах динамических систем необходимо делать ошибки, в этом (и только в этом) случае мы получим результат, правильно описывающий реальные процессы (в том числе необратимые).

При численных расчетах это условие соблюдается автоматически. Абсолютно точные теоремы (типа теорем об обратимости и теоремы Лиувилля) в случае неустойчивых систем приводят к результатам, не соответствующим действительности. В устойчивых системах малые ошибки роли не играют и оба подхода приводят к одинаковым результатам.
В принципе численные расчеты можно проводить и в системах, содержащих большое число частиц (порядка числа Авогадро), но практически это невозможно, да и не нужно. Проще использовать аппарат термодинамики.
Расчеты в рамках молекулярной динамики — пример редукции необратимых явлений к набору элементарных актов, описываемых фундаментальными законами физики.
В связи с этим уместно обсудить вопрос о тождественности частиц, который является одним из фундаментальных, как в квантовой, так и классической физике.