Математическое знание содержится в кратких высказываниях — математических структурах. Возникает вопрос: содержат ли новую информацию доказательства теорем? Вопрос не тривиален. С одной стороны, доказательство теорем приводится как классический пример творчества (то есть генерации информации). С другой стороны, теорема — следствие аксиом и, следовательно, не содержит новой (по сравнению с аксиомами) информации. Доказательство теоремы есть извлечение ценной информации из аксиом, то есть рецепция. Тем не менее, творческий элемент при доказательстве теорем, конечно, присутствует. Он связан с выбором пути доказательства. Как правило теорема может быть доказана несколькими способами. Выбор наиболее простого и доступного пути — генерация ценной информации.
Третье. Наиболее интересным и острым остается вопрос об условности (или безусловности) информации в естественных науках. Принято думать, что, изучая природу, мы рецептируем безусловную, вполне объективную информацию. Это действительно так, если речь идет об экспериментальных качественных результатах.
Например, информация о том, что одноименные заряды отталкиваются, а разноименные притягиваются, является безусловной. Математическое описание этого явления в виде закона Кулона было сформулировано на определенном языке (векторной алгебре). Выбор языка (кода) всегда условен. Можно было бы описать это явление на языке дискретных множеств или игр автоматов. Поэтому выбор математического языка — пример генерации условной информации.
Научное творчество в области естественных наук содержит два необходимых элемента: рецепцию безусловной информации от природы и генерацию условной (теоретической) информации. Успех зависит от того, в какой мере выбранный алгоритм описания уже принят в научном сообществе, то есть от тезауруса этого сообщества.

Начиная с работ по классической теории информации, установилась традиция связывать информацию с термодинамической величиной — энтропией. Начало этой традиции было положено Н. Винером, увидевшем действительно бросающееся в глаза сходство формул Шеннона для количества информации I и формулы Больцмана для энтропии S. Различие в размерности устранялось выбором единиц измерения I, которое можно измерять и в энтропийных единицах.
В дальнейшем появилось слово «негоэнтропия» и утверждение: «информация есть негоэнтропия» Эти слова многократно повторялись в научных статьях, книгах и даже в учебниках. У людей, занимающихся конкретными проблемами информатики эти слова вызывали (и продолжают вызывать) недоумение и раздражение (внутренний дискомфорт), потому, что «что-то в здесь не так».

В этом разделе мы обсудим что именно «не так» и почему.
Согласно определению (Q) информация есть запомненный выбор (т.е. макроинформация).
На физическом языке «запомнить», то есть зафиксировать информацию, означает привести систему в определенное устойчивое состояние. Ясно, что таких состояний должно быть не меньше двух. Каждое из них должно быть достаточно устойчивым, в противном случае система может самопроизвольно выйти из того или иного состояния, что равносильно исчезновению информации.

Простейшая запоминающая система содержит всего два устойчивых состояния и называется триггер (переключатель). Этот элемент играет важную роль во всех информационных системах.
В электронике в качестве запоминающего триггера используют магнитные домены (размеры порядка микрон), а также электрические и светочувствительные ячейки (тоже микронных размеров).

Свойством запоминания могут обладать только макроскопические системы, состоящие из многих атомов. Запомнить что-либо, располагая одним атомом, невозможно, поскольку атом может находиться лишь в одном устойчивом (основном) состоянии. То же относится и к простейшим молекулам. Наименьшая по своим размерам самая простая система, которая может запомнить один вариант из двух возможных, это молекула, способная находиться в двух различных изомерных состояниях при условии, что спонтанный переход из одной формы в другую может происходить так редко, что его вероятностью практически можно пренебречь. Примером таких молекул могут служить оптические изомеры, обладающие «левой» или «правой» киральностью, различающейся по способности содержащих их растворов вращать вправо или влево плоскость поляризации света, пропускаемого через растворы. К таким оптическим изомерам относятся сахара и аминокислоты, содержащие десять-двадцать атомов.
Молекулярными триггерами могут служить макромолекулы (в частности, белковые молекулы), способные существовать в нескольких (по крайней мере двух) конформационных состояниях.

Системы более высокого иерархического уровня, такие как клетка, популяция, организм, мозг, разумеется, тоже могут быть запоминающими. Механизм запоминания при этом не всегда сводится к генетическому (то есть макромолекулярному). Например, клетка (в частности, нервная), способная функционировать в двух и более устойчивых состояниях, уже является запоминающим устройством. Тоже можно сказать о популяции и организме. Механизм запоминания в нервных сетях (в частности, в мозге) имеет свои особенности, которые мы обсудим позже.
Важную роль играет время запоминания. В устойчивых динамических системах оно формально бесконечно. Переключить триггер из одного состояния в другое можно лишь за счет стороннего сигнала, что равносильно рецепции (см. выше). В реальности возможно спонтанное переключение (т.е. забывание исходного состояния) за счет случайных флюктуаций. Вероятность спонтанного переключения в единицу времени зависит от величины флюктуаций и высоты барьера F# между состояниями. В термодинамически равновесных (по микроскопическим степеням свободы) условиях эта вероятность равна:

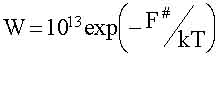Где: 1013 сек-1 — частота тепловых флюктуаций. Время запоминания Т= 1/W. При F# порядка 1.5 эВ время Т= 3•105 лет, что практически можно считать бесконечным.
Мы остановились на этом столь подробно, чтобы продемонстрировать:
Во-первых, макроинформация может содержаться только в макрообъектах.
Во-вторых, граница между макро и микро объектами проходит на уровне макомолекул, размеры которых порядка нанометров (10-9 метра или 10-7 сантиметра). Современная наноэлектроника подбирается к этой границе.

Наряду с макроинформацией выше упоминалось о микроинформации, которой соответствует выбор принципиально не запоминаемой. Примером последнего может служить выбор одного микросостояния идеального газа в состоянии термодинамического равновесия. Выбор микросостояния означает, что нам удалось в определенный момент времени t изменить координаты и скорости всех молекул с определенной точностью. Разумеется, это возможно лишь умозрительно, но и в этом случае выбранное состояние тут же (за время t~10-13 сек) , будет забыто, то есть сменится другим микросостоянием, выбранным по закону случая. Это свойство — забывать предыдущее микросостояние — является фундаментальным для эргодических систем. в которых средние по времени совпадают со средними по ансамблю. Именно оно понимается под словами «молекулярный хаос» и именно оно лежит в основе термодинамики.
Количество микроинформации в данном примере велико, согласно (1.3) оно равно:

где, nmicro число микросостояний , W=1/nmicro — вероятность случайно выбрать какое-либо одно из них. Количество макроинформации в том же примере, напротив мало; именно Imаcro= log2 nmаcro = 0, поскольку макросостояние равновесного газа единственно, то есть nmаcro = 1.
Разумеется, макроинформация не может быть ни ценной ни смысловой и вообще не может использоваться, как информация в реальной жизни. Тем не менее она широко обсуждается и является источником многих недоразумений.
Причину тому следующий:
Во-первых, формула (1.5) следующая из формулы Шеннона, очень похожа на формулу Больцмана для энтропии
.

(1, 6)

Где k=1,38 10-23 Дж/град. — постоянная Больцмана.
Поэтому микроинформация и энтропия пропорциональны друг другу:

(1.7)

В действительности формула (1.7) представляет собой связь между энтропией и микроинформационной емкостью (или «тарой»), поскольку сравниваются энтропия до измерения (S(t)) и количество микроинформации после измерения I(t+t).
Можно , (только умозрительно) оценить энтропию сразу после измерения, то есть до того как наблюденное состояние разрушится (т.е. в течение t @ 10-13 сек). С точки зрения термодинамики нахождение макросистемы в одном микросостоянии — колоссальная флюктуация. Энтропия ее много меньше равновесной энтропии S (до измерения). Именно:

где W(t1t+t) — условная вероятность того, что в момент t+t будет наблюдено то же макросостояние, которое реализовалась в момент t. Ясно, что W(t1t+t)=1 и S(t+t)=0.
Отсюда следует, что в результате измерения энергия уменьшалась на величину
DS=S(t+t)-S(t)=-S(t)
Количество информации до измерения, когда выбор еще не сделан Imicro(t)=0 , поэтому прирост количества макроинформации D Imicro=+ Imicro
Отсюда делается вывод:

(1.9)

Интерпретация выражения (1.9) такова: при увеличении информации о системе ее энтропия уменьшается. Отсюда же происходит крылатое выражение «информация есть негоэнтропия».
Во-вторых микроинформацию и энтропию связывает еще «демон» Максвелла.
Демон впервые появился более ста лет тому назад (в 1871 г.) в книге К. Максвелла «Теория теплоты», как парадокс, демонстрирующий возможность арушения второго начала термодинамики.
Напомним суть дела. Имеются два сосуда с газом при исходно одинаковой абсолютной температуре Т. Они разделены перегородкой, в которой имеется отверстие с заслонкой. Заслонкой управляет «демон», он фиксирует скорости и в одну сторону пропускает только быстрые молекулы, а в другую — только медленные. В результате через некоторое время в одном сосуде температура повышается, а в другом — понижается. Таким образом, тепло переходит от холодного тела к более теплому без совершения работы (на первый взгляд) — второе начало нарушается и энтропия уменьшается.

Разрешение парадокса было предложено известным физиком, много сделавшем дл развития теории конденсированных сред, Леоном Бриллюеном . Он показал, что даже демон бесплатно ничего не делает (так уж устроен наш мир). Для фиксации скорости молекулы, т.е. получению информации, демону нужно заплатить энергией, не меньшей, чем энергия теплового кванта kT (при комнатной температуре Т=300оК, kT= 0,025 эВ). Энергия kT/1,44 — минимальная цена одного бита микроинформации (1,44 — коэффициент перехода от натуральных логарифмов к двоичным). После этого стало ясно, что демон совершает работу и как раз такую, которая необходима для охлаждения одого тела и нагревания другого. По существу любой домашний холодильник работает как демон и за это тоже нужно платить.
При этом демон получает информацию равную уменьшению энтропии. Так возникло утверждение: «информация есть негоэнтропия». Приставку «микро» при этом по недосмотру опустили, а зря, поскольку именно это привело к серьезным недоразумениям.
Разрешение парадокса всегда вдохновляет. Поэтому среди физиков — последователей Бриллюена — демон и слово «негоэнтропия», как синоним информации, стали часто употребляться — возник миф о негоэнтропии.

Справедливости ради, следует заметить, что Бриллюэн различал свободную информацию (не давая ей, к сожалению, четкого определения) и связанную информацию, возникающую, когда возможные случаи «могут быть представлены как микросостояния физической системы». И далее: «Только связанная информация будет представляться связанной с энтропией». Отсюда ясно, что, во-первых, на деле Бриллюэн не приписывал любой информации свойства негэнтропии, а во-вторых, ограничивал свое рассмотрение только той частью информации, которая связана с микросостояниями. Так что к недоразумению привели не сам Бриллюен, а его эпигоны.
После этих разъяснений формализм Бриллюэна выглядит очень просто и результаты расчетов соответствуют (1,9).
Реально ни физического, ни информационного содержания термин «негэнтропия» не имеет (он от «демона»). Что же касается той информации, которой занимался Бриллюэн, то сам он называл ее «связанной»; в отечественной литературе принят термин «микроинформация».

Микроинформация существенно отличается от макроинформации, поскольку она не имеет важного для информации свойства фиксируемости, ибо незапоминаема.
Макроинформация существенно отличается от микроинформации не только качественно, но и количественно. Это ясно, если вернуться от энтропийных к обычным единицам измерения информации — битам.

Iмикро — огромное число, ибо k = 1,38 Ч10-23 Дж/К (DS < 0) ,
Iмaкро << — (DS/k)log2e
Причина этого неравенства в том, что запоминание — процесс макроскопический и диссипативный, он сопровождается большим изменением энтропии.
Количественное различие ясно из следующих соображений.
Формула (1.3) справедлива как для микро-, так и для макроинформации, но существенно различны числа возможных вариантов n . В случае макроинформации n — число устойчивых состояний системы, оно, как правило, невелико. В случае микроинформации n — полное число микросостояний, (неустойчивых, то есть микроскопических) — оно огромно.

Яркий пример тому приведен в книге Блюменфельда «проблемы Биофизики» [25]. Показано, что вся информация, заключенная в человеке (включая ДНК, белки, а также мысли, как тайные, так и явные), будучи выраженной в энтропийных единицах, соответствует энтропии испарения одного пол-литра кипяченой воды (на самом деле, не так уж важно, чего именно)
Всякий раз, когда в акте творчества создается новая ценная информация, мы имеем дело с макроинформацией. Из книг, лекций, природы мы рецептируем макроинформацию. Вообще в реальной жизни, в частности, в биологии всегда используется макроинформация, которую мы в предыдущих и в последующих разделах называем просто информацией.

Любое изменение макроинформации, увеличение или уменьшение, сопровождается ростом энтропии, что естественно, поскольку эти процессы необратимы. Количественной связи между изменениями макроинформации и физической энтропии не существует. Энергетическая цена макроинформации, конечно, существует, она определяется энергией, диссипирующей в процессе запоминания и зависит от конкретных условий, в частности от времени на которое информацию нужно запомнить, то есть от свойств ячейки памяти. Эта энергия, приходящаяся на один бит информации, заведомо (и много) больше кТ/1,44 — энергии одного бита микроинформации.
Таким образом, слово негоэнтропия — появилось в результате непониманя роли условия запоминания информации. Слово негоэнтропия — пример условной информации, которая в действительности не ускорила, а, напротив, затруднило исследование информационных процессов, то есть оказалась на деле дезинформацией. Именно от этого предостерегал Шеннон, слова которого мы уже приводили выше.
В заключение раздела обсудим ещё одно недоразумение, связанное с понятием «порядок». Часто можно встретить утверждение о том. что информация — мера упорядоченности, оно фигурирует даже в коллекции определений.

Это утверждение воспринимается как объективное (безусловное). На самом деле требуется уточнить. какая именно информация (ценная или нет, условная или безусловная) имеется в виду. Надо уточнить также, что понимается под словом «порядок». Без этих уточнений утверждение теряет смысл.
В действительности в приведенном утверждении неявно предполагается, что информация ценная, но в этом случае она наверняка условная, ибо зависит от цели.
Понятие «порядок» тоже целесообразно. Так, если цель — прогноз, то упорядоченными следует считать системы, развивающиеся устойчиво и допускающие предсказание результатов. Именно в этом смысле в физике хаотические системы считаются беспорядочными и энтропия здесь выступает как мера беспорядка.
В более общем случае, когда преследуются иные цели, меняется и смысл слова «порядок».
Для иллюстрации приведем пример из жизни.

Пусть некто (писатель или ученый) пишет книгу. Для этой цели он расположил материалы в определенном порядке: рукопись — на столе, черновики — под столом, статьи и книги — на стуле и диване. В кабинет входит жена и приходит в ужас, поскольку у неё другие цели и другое представление о порядке. Представьте, что ученый отлучился на время, а когда вернулся жена встретила его радостными словами: «я, наконец-то навела порядок в твоем кабинете». Представить состояние ученого в этот момент уже не трудно.
Из этого примера следует, что порядок — понятие условное в той же мере, как и ценная информация.
Утверждение: «Ценная информация есть мера условного порядка» имеет четкий смысл, оно правильно и. более того, банально. Отсюда ясно, что искать объективную меру объективного порядка бессмысленно, ни того, ни другого просто не существует.
В действительности проблема порядка и хаоса имеет много аспектов и к ней мы ещё вернемся в гл. 7.
В заключение главы отметим, что:
Все (или почти все) определения, приведенные в «коллекции» имеют смысл и относятся к разным сторонам информационного процесса.
Объединить эти определения, увидеть общую картину информационного процесса и понять суть феномена информации позволяет теория динамических систем, или, что то же, синергетика.
Это не случайно, развивающиеся сложные системы имеют много аспектов. В гуманитарных науках это свойство предстоит как многоликий образ — термин яркий эмоциональный, метафорический, но не четкий. В синергетике то же предстоит вполне конкретно, как мультистационарность [27] или, что то же, многовариантность [34], многомодальность [35], В синергетике эти понятия формулируются четко и конструктивно, так, что с ними можно работать

Одна из особенностей нелинейной динамики открытых неравновесных систем (синергетики) состоит в том, что она имеет дело с неожиданными событиями. Эти события проявляют себя как качественные скачкообразные изменения состояния системы или режима ее развития в ответ на монотонное и медленное изменение параметров. При анализе всякий раз выясняется, что причиной неожиданности оказывается неустойчивость.

В этом разделе мы приведем основные сведения и поясним понятия теории динамических систем (или, что то же , качественной теории дифференциальных уравнений). Полное изложение можно найти в соответствующих математических учебниках [1-5]. Популярное изложение содержится в книгах [6 - 9]
Теория динамических систем, основана на дифференциальных уравнениях вида:
dui/dt = (1/ti) Fi(u1 , u2, …un) , (2.1)
где ui — динамические переменные, например, концентрации реагирующих веществ, Fi(ui) — нелинейные функции, описывающие их взаимодействие. ti — характерные времена изменения переменных ui , i = 1, 2, … n.
Уравнения (2.1) являются динамическими, то есть при задании конкретного вида функции Fi их решения, вообще говоря, однозначно определяются начальными условиями Казалось бы в такой ситуации ничего неожиданного быть не должно. Тем не менее характерные для синергетики неожиданности здесь возникают, когда решения динамических уравнений теряют устойчивость.

Анализ устойчивости уравнений движения (изменения), а также устойчивости стационарных состояний основан на исследовании поведения малых отклонений от соответствующего решения . Покажем это на примере стационарных состояний системы частиц (точек).
Стационарными называются состояния, соответствующие таким значениям переменных u1 , u2, …un , при которых все функции Fi(u1 , u2, … un) равны нулю. При этом значения ui не меняются со временем, так как все производные (см. 2.1) также равны нулю. Однако малые отклонения от стационарных значений dui изменяются со временем, и их изменение можно описать системой линейных дифференциальных уравнений:

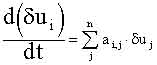(2.2)

где:

при uj = `uj , `uj — стационарные значения переменных.

Решения системы (2.2) имеют вид:

(2.3)

Здесь коэффициенты ei i определяются из условий:

(2.4)

Откуда следует, что они пропорциональные начальным отклонениям, (e ~ du(0)) и малы в меру малости последних. Величины li — числа, которые являются решениями алгебраического уравнения: det| ai,j — dij li| = 0, где dij — символ Кронекера такой, что dij = 0 , если i № j и dij = 1 при i = j. Величины li играют важную роль в теории устойчивости, их называют числами Ляпунова.
Если числа Ляпунова отрицательны, то все dui(t) убывают со временем, поэтому состояние устойчиво. В этом случае система стремится обратно к стационарному состоянию, даже, если ее немного отклонить от него. Если хотя бы одно из чисел Ляпунова положительно, то состояние неустойчиво.
В общем случае числа Ляпунова могут быть комплексными. Устойчивость определяется тогда знаком действительной части. Если среди чисел Ляпунова имеются равные нулю или чисто мнимые, то стационарное состояние называется нейтральным; при отклонении от него не появляются ни возвращающие, ни отклоняющие силы.
Анализ неустойчивых движений основан на том же принципе: определяется временнaя зависимость малых отклонений от заданной траектории. Используются линейные по отклонениям уравнения (высшими степенями dui(t) пренебрегают), решения которых имеют вид:

(2.5)

Числа Ляпунова при этом уже не постоянны, а зависят от времени. Траектория является неустойчивой, если среди чисел li(t) имеются такие, вещественные части которых положительны в достаточно большом интервале времени Dt, таком. что Dt l(t) >> 1.
Подчеркнем важное свойство: числа Ляпунова являются характеристическими (или собственными) числами системы; они не зависят от начальных условий. Таким образом, устойчивость (или неустойчивость) — внутреннее свойство исследуемой системы, а не результат внешнего воздействия. Особенность его в том, что проявляется оно только при наличии малых внешних воздействий.
Эта особенность привела к важным методологическим последствиям. Сейчас приходится пересматривать и подвергать ревизии некоторые, казалось бы установившиеся в физике понятия. Обсудим три примера.

Рассмотрим понятие абсолютно изолированной системы. Сейчас ясно, что его можно (и то не всегда) ввести лишь как предел неизолированной системы при стремлении к нулю величины внешнего воздействия. Для устойчивых систем такой предел существует и, следовательно, понятие остается в силе. В неустойчивых системах такой предел, вообще говоря, не существует. Действительно, предел величины du(t) = eЧ еlt (где l > 0) при e ® 0 и t ® µ зависит от порядка стремления аргументов к своим пределам. Формально величину e (которая отражает меру внешних воздействий) и время t можно считать независимыми. Однако, как мы убедились на конкретном примере, уже при сравнительно небольших временах фактор еlt возрастает столь сильно, что компенсировать его уменьшением e — задача абсурдная. Суть дела здесь в том, что экспоненциальная зависимость (explt) очень сильна, конкурировать с ней практически невозможно. Поэтому для неустойчивых систем понятие «абсолютно изолированная система» теряет смысл; можно говорить об относительно изолированной системе.

В связи с явлением неустойчивости возникает необходимость пересмотреть такие понятия как «бесконечно малое» и «бесконечно большое». Ясно, что при небольших временах (таких, что t»1/Rel ) и Dx<<1, то есть отклонения малы, и возмущением можно пренебречь. При этом динамическим расчетам можно доверять даже в случае их неустойчивости. Время t»1/Rel называется интервалом предсказуемости (или горизонтом прогнозирования).

Ясно также, что при больших временах (таких, что Rel•t =100 — 1000) отклонение Dx(t) станет большим при любых реальных возмущениях Действительно, для того, чтобы пренебречь возмущениями в этом случае необходимо изолировать систему с точностью до , что невозможно.
Здесь не обсуждалось, какую размерность имеют величины Dx(t) и Dx0 и в каких единицах они измерены. В данном случае это и не важно. Дело в том, что любые физические величины (длины, массы, временные интервалы, числа частиц и т. д.) в нашем мире ограничены, то есть выражаются числами в интервале от 10-100 до 10+100 . Большие (или меньшие) числа могут появиться лишь как результат расчета, в котором фигурирует экспоненциальная (или более мощная ) функция. В связи с этим Эдваром Каснером было введено новое понятие «гугол» — столь большое число (больше 10+100 ), которое не может соответствовать никакой физической величине (см. [10])

Возмущение является физической величиной. Отсюда следует, что начальное отклонение не может быть меньше 10-100 , в то время как величина Rel•t вполне может стать больше 100. Обратный «гугол» , хотя формально является конечной величиной, реально должна рассматриваться как бесконечно малая. В частности, вопрос: как ведет себя функция внутри интервала порядка обратный гугол, лишен смысла. Функцию на таком интервале следует заменить числом (средним по интервалу), поскольку более детальное её поведение принципиально не наблюдаемо. Это утверждение. хотя и негативно, играет важную практическую роль. что мы продемонстрируем позже.
Требует ревизии и понятие «причины» [11,12]. Обычно под причиной понимают начальные условия (или импульсные внешние воздействия), которые в соответствии с динамикой системы приводят к определенному результату, т.е. — следствию. На этом языке слово «вскрыть причинно-следственные связи» означают «понять динамику промежуточных процессов». При этом негласно предполагают, что причины и следствия соизмеримы. Для устойчивых (или нейтральных) процессов это всегда имеет место. В неустойчивых процессах ситуация иная: очень малая величина приводит к следствию, которое по масштабам с причиной не соизмеримо. Обычно в таких случаях говорят, что причиной явилась неустойчивость, а не малое начальное воздействие. При этом, однако, происходит весьма существенный сдвиг понятий: в качестве причины фигурирует внутреннее свойство системы, а не внешнее воздействие.

Поясним сказанное на житейском примере. Рассмотрим два случая. В первом хрустальная ваза стоит на середине стола (состояние устойчиво). Прошел некто и неловким движением столкнул вазу со стола — она разбилась. В чем причина столь печального события, или, другими словами, кто виноват? Ясно, что виноват «некто» а причина — его неловкое движение.
Рассмотрим другой случай: ваза стоит на краю стола так, что чуть не падает (состояние, близкое к неустойчивому). Пролетела муха — ваза разбилась. В этом случае муху не обвиняют, а говорят, что причина события в неустойчивом положении вазы. Виноват тот, кто ее поставил (так, чтобы никто не был виноват, в жизни обычно не бывает). Забегая несколько вперед, отметим, что в основе утверждения «событие произошло случайно» (то есть без видимой причины) также лежит неустойчивость динамических процессов.
В общем случае выход из неустойчивого состояния возможен в разные стороны. Так, шарик, движущийся по водоразделу, может свалиться как вправо, так и влево. Направление зависит от начального возмущения.

В отсутствии выделенного направления принимается, что малые возмущения равновероятны. Здесь мы впервые употребляем слово «вероятность». В устойчивых динамических системах оно не употребляется и, более того, не имеет смысла. В неустойчивых системах, напротив, достоверные предсказания не имеют смысла, и можно говорить лишь о вероятности того или иного результата. Таким образом, неустойчивость является тем свойством, которое позволяет ввести в динамическую теорию понятие «вероятность».
Из изложенного следует, что устойчивость (неустойчивость) — не просто одно из свойств динамической системы. Это свойство существенно расширяет и изменяет аксиоматику динамических систем и позволяет взглянуть на мир с иной точки зрения. Ярким следствием неустойчивости является «динамический хаос».
Вернемся к системе уравнений (2.1).

При исследовании открытых систем, способных к самоорганизации, в качестве динамических переменных ui выступают самые различные величины: потенциалы и токи в физике, концентрации различных веществ в химии, численности организмов разных видов в биологии и экологии. Число переменных в реальных системах достаточно велико. Исследовать свойства многомерных систем сложно.

На помощь приходят методы редукции, т. е. сведения системы уравнений, содержащих большое число дифференциальных уравнений (и, следовательно, переменных) к более простой системе из меньшего числа уравнений. Редуцированную систему уравнений называют базовой. От неё требуется:
Во-первых, чтобы она описывала основные черты рассматриваемого явления.
Во- вторых, чтобы она содержала минимальное число переменных и параметров.
В-третьих, чтобы она была «грубой» в смысле Андронова. Последнее означает, что при малом изменении параметров и слабом расширении базовой системы (то есть добавлении высших производных и/или новых членов с малыми коэфициентами), решения должны меняться мало.

В химической кинетике редукция кинетических уравнений использовалась давно и известна как метод стационарных концентраций. Он основан на временной иерархии процессов. Последнее означает, что характерные времена ti в (2.1) существенно различны и их можно разделить на три группы. К первой относятся процессы, времена которых совпадают с характерными временами интересующего нас явления. Ко второй относятся медленные (по сравнению с первыми) процессы и к третьей — быстрые.
Например, если нас интересуют изменения системы, происходящие за 1-10 минут, то процессы, протекающие за секунды и доли секунд считаются быстрыми, а процессы, для которых требуются часы и сутки — медленными. Иная градация возникает, если нас интересуют секундные изменения; тогда минутные процессы мы уже отнесем к медленным.

Разбив реакции на такие группы, мы можем заметить следующее:

1. Все медленно и очень медленно изменяющиеся концентрации мы просто можем считать постоянными и равными их начальным значениям.
2. В быстрых и очень быстрых реакциях успевают установиться стационарные концентрации.

Другими словами, между соответствующими концентрациями быстро установятся определенные соотношения и при изменении одной из них другие почти мгновенно к ней подстроятся. В этом случае часть дифференциальных уравнений можно заменить алгебраическими соотношениями и система упростится.
В результате останутся лишь процессы, имеющие примерно одинаковые скорости; их, как правило, не много. Замену дифференциальных уравнений алгебраическими называют иногда принципом стационарных концентраций.
Строгое математическое обоснование такой процедуры было дано А.Н.Тихоновым [13] . Мы не будем здесь приводить доказательство этой теоремы, ограничимся лишь примером.
Пусть среди n компонентов процесса имеется такой (концентрацию его обозначим u1), который очень быстро образуется, но очень быстро расходуется. Тогда уравнение для него можно записать в виде:

где А = 1/ t1 >>1

(2.6)

Учитывая, что за времена порядка t1 все концентрации, кроме u1, изменяются слабо и считая их постоянными, можно найти стационарную концентрацию `u1 из условия:

(2.7)

Используя (2.7) можно выразить `u1 через другие переменные и таким образом сократить число дифференциальных уравнений.
На первый взгляд это может показаться парадоксальным. Действительно, приравнивая нулю функцию F(ui,) мы как бы считаем, что скорость изменения u1 равна нулю, хотя с другой стороны именно она пропорциональна большой величина А.
Не трудно убедиться, однако, что парадокса тут нет, если стационарное состояние уравнения (2.6) устойчиво. Последнее является необходимым условием теоремы Тихонова, если оно не соблюдается, то использовать метод стационарных концентраций нельзя.
Для демонстрации этого рассмотрим решение уравнения (2.6), в случае малых отклонений u1 от стационарного значения. В данном случае выражение (2.3) принимает вид:

где ;

(2.8)

Устойчивость решения уравнения (2.6) означает, что частная производная в (2.8) отрицательна. Число Ляпунова при этом тоже отрицательно и очень велико (поскольку А>>1). Это обстоятельство обеспечивает быстрое установление стационарного значения концентрации u1 , что и является основным утверждением теоремы Тихонова.
При моделировании конкретных сложных систем (например, экологических) сначала исследуют базовую модель и затем её расширяют до полной, которая называется имитационной. Последняя дает те же результаты, что и базовая, но кроме того позволяет описать поведение «деталей», то есть тех быстрых переменных, которые в базовой модели не фигурируют.
Во многих и очень важных случаях базовая модель содержит всего два уравнения. Для исследования их используется наглядный метод построения так называемого фазового портрета.
Поясним его смысл на примере двух уравнений для переменных x и y.

(2.9)

P(x,y) и Q(x,y) известные и в общем случае нелинейные функции своих переменных.
На рисунке 2.1 приведена плоскость (x,y). Каждая точка на этой плоскости дает информацию о состоянии системы (2.9) и потому называется изображающей точкой.
Пусть в начальный момент t=0 переменные x и y равны x=x1 ; y=y1 . Вычислим их приращения за малый интервал времени Dt. Эти приращения отложены на рисунке (2.1). Там же приведен вектор смещения изображающей точки. Аналогично можно вычислить смещение в следующий интервал времени. Повторяя процедуру можно получить ломаную линию, которая при Dt®0 переходит в плавную кривую, именуемую траекторией системы. Движение изображающей точки по траектории дает представление о развитии процесса во времени, даже если точное решение системы (2.9) не известно или не может быть выражено в аналитической форме. Именно в этом заключается ценность фазового портрета.

Для упрощения расчетов удобно провести две линии P(x,y)=0 и Q(x,y)=0. На первой приращение Dx=0, то есть траектории на ней вертикальны. На второй приращения Dy =0, то есть траектории на ней горизонтальны. Эти линии называются главными изоклинами. Точки их пересечения соответствуют стационарны состояниям, поскольку при этом оба приращения равны нулю.

На этом примере удобно проиллюстрировать теорему Тихонова и прояснить некоторые математические тонкости. Последние заключаются в следующем:
i) Полная система уравнений содержит n переменных и требует задания стольких же начальных условий. В редуцированной системе число переменных и начальных условий меньше, то есть часть условий оказываются лишними.
ii) При редукции нарушаются аналитические свойства решения полной системы.
Поясним это на примере редукции системы (2.9) в случае когда tx >> ty . Cогласно теореме Тихонова систему (2.9) можно редуцировать до одного уравнения:

(2. 10)

где зависимость y(x) — решение алгебраического уравнения Q(x,y) =0.