Рыжов В.А. канд.физ.-мат.наук, X-treme Infomatics

Курдюмов В.С. - зам. директора Института экономических стратегий; Гендиректор АНО “Центр междисциплинарных исследований” (ЦМИ)

Введение

Вектор интересов современной науки в проекции ее актуальных проблем сейчас разворачивается в сторону новых еще не освоенных просторов знания о динамической сложности и самоорганизации [1]. Этот научный натиск и желание понять нелинейную динамику высокоорганизованных и сверхсложных систем бросают серьезный вызов научному сообществу [2, 3]. Пока никто еще не проник в тайну таких сложных систем, как живые организмы с их клетками и биосферой, или социум с его развитием и эволюцией, а также сообществами и малыми группами. Много еще непонятного и в происхождении естественных языков, не всё понятно, в чем состоит сущность знаний, коими инструментами мы пользуемся в своём познании. К сожалению, даже современный научный метод с его существующими математическими парадигмами (в свое время так удачно сформировавший естественные науки) оказался не совсем пригодным для освоения сверхсложности [4]. Наверняка придётся преодолевать трудности по всему этому широкому фронту. В данной работе мы сделаем акцент на развитии математических парадигм.

Математика – это инструмент для расширения возможностей интуиции и мышления человека посредством математических образов, а также её формальных методов и правил. Математические модели раньше обычно записывались, на бумаге, например, в виде формул отношения или баланса с различными параметрами. Также давно используются различные геометрических объекты – от плоских до стереометрических форм и топологий. В настоящее время широко используются различные схемы, диаграммы, графики и прочие визуальные иллюстративные объекты. Однако все они не очень-то годятся для целей, поставленных выше. Даже средств дискретной математики, нацеленных на структурный, функциональный и логический анализ различных систем, явно недостаточно. Кстати, даже информатика, породившая новую экономическую формацию и цифровой бум в промышленности, науке, индустрии, образовании и прочих сферах жизни общества, пока еще далека от готовности к штурму сверх сложности. Хотя мы уже начинаем понимать, что к сложности необходимо подходить с позиции междисциплинарности. Здесь все важно: физические и химические взгляды с их энергиями, полями, силами и прочими факторами структуры материи; био-медицинские взгляды с их непосредственным исследованием сложности; различные гуманитарные науки с их также непосредственным исследованием сложности. Единственно, где преуспела математика – это физические, химические науки и, конечно же, технические дисциплины. Немного особняком стоит информатика. Парадокс информатики в том, что информационные технологии проникли практически во все отрасли человеческой жизни, даже построено информационное общество, а вот с основаниями информатики пока еще не разобрались. Например, нет достаточно формализованных понятий информации и знаний, за исключением только узких теорий – логика, передача информации, алгоритмы. А вот искусственный интеллект (не отдельные алгоритмы) так и остался в зачатке. В данной ситуации наиболее интересное направление в основаниях математики и куда следует двигаться – это раздел дискретной математики. Конечно же, не следует отрицать значимости и других направлений.

Проблемы изучения сложных систем и математические вызовы

Знания о системной сложности в современной науке стали более востребованы. Определение сложной системы – важный элемент знания, требующий междисциплинарного подхода. Освоение сложности это передовые рубежи современной науки, особенно в области биологии, социологии и управления сложными системами. Классическое образование и фундаментальные науки не затрагивали вопросов системной сложности, поэтому сложилось междисциплинарное направление научных исследований – синергетика. Задачи синергетики сосредоточены на познании общих закономерностей возникновения, развития и принципов самоорганизации, лежащих в основе процессов в сложных системах самой разной природы.

Научное сообщество уже прошло этап эмпирического развития интуиций в виде отдельных попыток поработать с термином “сложная система”. Теперь на очереди практический, научно обоснованный подход, состоящий в создании работающих математических конструкций и технологий исследования системной сложности.

Предлагается включить в категорию “Системная сложность” комплекс базовых парадигм: Целостность, Модульность, Фрактальность, Мембраны, Динамическое равновесие, Самоорганизация и параметры порядка, Гомеостаз, Эволюционность, Информационность, Целеустремленность, Самовоспроизведение (автопоэзис), Сознание. Более подробно с этими парадигмами можно познакомиться в Приложении в конце статьи. Одно из свойств системной сложности состоит в том, что каждая из перечисленных парадигм генетически содержит в себе все остальные парадигмы. Естественно, что этот список не является исчерпывающим, а в зависимости от поставленных задач, может изменяться и добавляться.

Структура сложной системы состоит из множества составляющих ее частей (подсистем). Подсистемы могут взаимодействовать между собой в соответствии с их внутренней целесообразностью (функционалом). При этом сложная система имеет новые эмерджентные свойства, которые отсутствуют у её частей. Это первая зацепка. Сложную систему не удается описать простыми определениями. Также не удается описать ее структуру соответствующими математическими моделями, а поведение – математическими уравнениями. Для этого пока еще не хватает возможностей современной математики [5].

На пути исследования системной сложности стоят большие интеллектуальные трудности. Очевидно, что потребуется много усилий и большая глубина проникновения интуиции, мышления в проблемные области системной сложности. Одна из проблем – высокая перегруженность формализмом в современной математике для определений первичных понятий и для описания математических объектов. Что часто уводит исследователя от смысла предмета исследования и заставляет глубоко сосредотачиваться на формальных описаниях, допуская ошибки и методологические промахи. Всё это сильно ограничивает интеллектуальную и выразительную мощность математики. Конечно, современные компьютерные средства и информационные технологии динамического моделирования продвинулись далеко вперёд. В частности разработано множество инструментов, методов и средств визуализации, включая алгоритмы преобразований структур данных и синтез виртуальной реальности. Но реликт плоского и статичного мышления все еще преследует и тормозит современную мысль, заставляя старыми стереотипами мышления отдавать дань прошлому.

Диалектика развития науки состоит из цепи противоречий. На определённых этапах эволюции науки возникают сложности и противоречия, требуя отказаться и разрушить старые стереотипы. Чтобы преодолеть противоречия, нужны прорывные идеи. Вместе с новыми идеями приходят новые теории и возможности освоения нового смыслового пространства на основании новых парадигм [6]. После небольшого устойчивого развития опять достигается предел существующих знаний. Поэтому резко накапливаются противоречия. И опять возникает необходимость вырваться из границ устаревших знаний. Что снова требует разрушения установленных стереотипов. Так эти циклы повторяются в развитии по спирали восхождения через отрицание старого к новым идеям, теориям и знаниям. Решающую роль в таком эволюционирующем развитии науки играют новые научные парадигмы в основаниях математики. Именно в основаниях математики с её новыми элементами следует искать главный катализатор мышления, приводящий к научным открытиям.

В математике сейчас очередной кризис переходного периода. В старых знаниях ощущаются ограничения, а для новых знаний еще не найдены нужные когнитивные образы, не нащупаны новые оригинальные парадигмы. Сейчас необходим новый математический язык, чтобы создать адекватные образы и описать элементы нелинейной динамики сложности. Пока идет интуитивный поиск новых объектов математики, в зону интересов попадают следующие феномены сложных систем:

1. Самоорганизующийся хаос (возникновение порядка из хаоса, баланс между устойчивостью и неустойчивостью в динамическом состоянии систем).
2. Жизненный цикл развития сложных систем (зарождение, развитие, переход в другое состояние или смерть).
3. Фазовые и структурные переходы между различными динамическими состояниями (генезис сложных систем, системные метаморфозы, различные режимы: обострение, стагнация, пульсация и пр.).
4. Поле путей развития системы и системное время (аттракторы, бифуркации, формирование многообразия поля путей развития системы, выбор траектории развития и пр.).
5. Гомеостаз системы (реакция на локальные изменения и глобальная адаптация на перспективу).
6. Фрактальная динамика развития систем в иерархическом ракурсе “части-целого” (локальные и глобальные параметры порядка, горизонтальные и вертикальные границы фрагментов).
7. Циклодинамика субъекта и объекта управления (процессы переноса вещества, энергии, информации).
8. Системное время, события (темпомиры и границы между ними).
9. Мембраны между внутренней и внешней средой (избирательная и барьерная проницаемость {рецепторная, энергетическая, информационная}, транспортный обмен, сигнальный обмен, регуляция и пр.).

В данной работе предприняты усилия в области дискретной математики с целью поиска дополнительных возможностей моделирования сложных систем. Развитие математического аппарата теории графов и сетей Петри создаёт новые опорные образы мышления и воображения для моделирования. Например, для исследования процессов, структуры и динамики событий, особенно необходимых для изучения свойств сложных динамических нелинейных систем. Это даёт возможность конструктивно взглянуть на информационные процессы в сложных иерархических системах, включая темпомиры и автопоэзис.

Графы, расширения и их опорные образы мышления

Определим для начала конечные графы [7], чтобы с их помощью определить нужные нам расширения графов. Граф это модель в системы, в которой выделены объекты и простые парные связи между этими объектами. Объекты графа называются вершинами, а связи между двумя объектами называются ребрами. Пример графа из семи вершин и десяти рёбер показан на Рис.1. Например, вершины v₂ и v_7, соединяются ребром e₈. Дадим определение графа как принято на языке теории множеств.

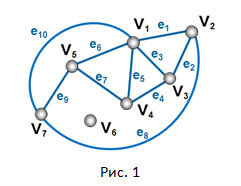
Определение. Конечный граф это система G = (V, E), которая состоит из конечного множества вершин V = {v_1, v_2, v_{3, …} v_n} и конечного множества связей (рёбер) между ними E = {e_1, e_2, e_{3, …} e_m}. Каждому ребру соответствует пара вершин: если ребро (u, v) соответствует ребру e, то говорят, что e инцидентно вершинам u и v.

Ребро e называется ориентированным, если пара его вершин упорядочена e = (u, v), то есть ребро e ориентировано из вершины u в вершину v. На диаграмме графа ориентированное ребро обозначается стрелкой в соответствующем направлении. Графы могут быть частично ориентированными, то есть, иметь неориентированные и ориентированные рёбра (см. Рис.2). Например, ребро e₁ – неориентированное, а ребро e₁₁ – ориентированное (от вершины v₁ к вершине v_2,). Графы с полностью ориентированными рёбрами называются орграфами. Ребро называется петлей, если оно начинается и кончается в одной и той же вершине. Например, на Рис.2 у вершины v₅ имеется петля e₁₄, а параллельными рёбрами являются e₁ и e₁₁, e₅ и e₁₂, e₉ и e₁₃.

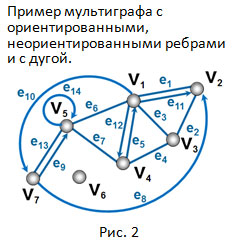
Назовём два ребра кратными, если они имеют одну и ту же пару концевых вершин (и если они имеют одинаковую ориентацию в случае ориентированного графа). Например, ребро eориентировано параллельно ребру f, если e = (u, v), f = (u, v). Граф называется простым, если он не имеет ни петель, ни кратных ребер.

В графе G = (V, E) будем обозначать |G| — количество вершин, а |V| — количество рёбер.

Говорят, что вершины v_i и v_j в графе смежные, если существует ребро e = (v_i, v_j), соединяющее их. Говорят, что два ребра e₁ = (u,v) и e₂ = (v,q) смежные, если они имеют общую вершину — v.

Простой путь, или для краткости, назовём его просто путём, будем записывать как (v_1, v_2, v_{3, …} v_k), — это последовательность смежных ребер (v_1, v₂), (v_2, v₃), (v_3, v₄), _… (v_k-1, v_k), в которой все вершины v_1, v_2, v_{3, …} v_k различны. Если v₁ = v_k, то такой путь называется циклическим. В неориентированном графе такой путь называется неориентированным путём из v₁ в v_k. В орграфе такой путь называется ориентированным путём из v₁ в v_k. Число ребер в пути называется длиной пути. Путь наименьшей длины называется кратчайшим путем. Замкнутый путь называется циклом.

Граф G называется связным, если между любой парой его вершин v_i и v_j существует хотя бы один путь.

Граф G^~ = (V^~, E^~) называется подграфом графа G = (V, E), если V^~  V, а E^~  E.

Гиперграфы. В сложных открытых системах, таких как биологические или социальные объекты, например, при моделировании многоклеточных структур организма или малых групп в сообществе, часто возникает задача выделить несколько уровней взаимодействия между субъектами. Межличностные отношения – хорошо отображаются простыми рёбрами (ориентированными или нет), параметры порядка группы – отображаются гиперсвязями, в которых задействованы все участники группы. Причём, таких параметров порядка в группе может быть несколько, как, например, на Рис.3. Пример показывает: две группы А и Б, включая пять субъектов вне этих групп; три групповых параметра порядка (для каждой группы свой и один общий – показаны тремя цветными овалами); одну связь между группами на уровне их параметров порядка (зелёная дуга); а также три типа различных межличностных связей (другие цветные дуги).

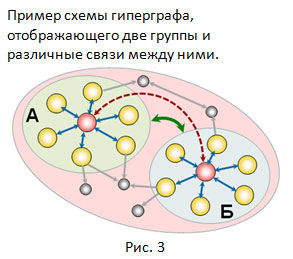
Мы видим, что при моделировании в системе между объектами необходимо устанавливать связи не только между парами объектов, как в обычных графах. Например, возникает потребность описывать более сложные связи между объектами в количестве более двух. Если в системе присутствуют связи, объединяющие объекты в количестве p≥3, то модель графа, показывающего такую структуру связей, называется гиперграфом степени p.

Определение. Гиперграф степени p – это граф G^p = (V, E), который состоит из конечного множества вершин V = {v_1, v_2, v_{3, …} v_n} и конечного множества связей (гипер-рёбер) между ними E = {e_1, e_2, e_{3, …} e_m}. Каждому ребру e_i(i[1:m]) соответствует множество вершин {v_i1, v_i2, v_{i3, …} v_1r}, где (1≤r≤p). Иными словами, связи (гипер-рёбра) гиперграфа G^p могут связывать до p вершин одновременно.

На Рис.4 показан гиперграф третьей степени G³ = (V, E), где V = {v_1, v_2, v_{3, …} v₈}, E = {e_1, e_2, e_3, e_4, e_5, e_6, e_7, e₈}, а e₁ = (v_1, v₇), e₂ = (v_2, v₇), e₃ = (v_1, v_2, v₅), e₄ = (v_1, v_2, v₃), e₅ = (v_4, v_6, v₇), e₆ = (v_7, v₄), e₇ = (v_4, v₅), e₈ = (v_1, v₈).

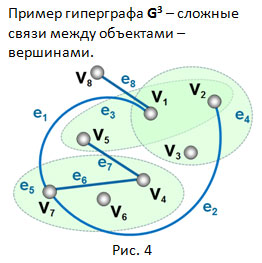
Например, у этого гиперграфа имеется восемь связей между восемью вершинами: пять обычных рёбер e₁, e₂, e₆, e₇ и e₈, а также три гипер-ребра третьей степени – e₃, e₄, e₅ (показаны пунктирными овалами зелёного цвета). У этого гиперграфа все вершины за исключением v₈ имеют гиперсвязи.

Вложенные графы. При построении модели гиперграфа мы акцентировали своё внимание на возможности построения и визуализации сложных связей между простыми объектами — вершинами. Мы не вникали в строение объектов – вершин графов, а развили детализацию в сторону усложнения связей между вершинами по принципу – “от простого к сложному”. Теперь по аналогии с усложнением связей можно акцентировать своё внимание на детализации строения самих вершин графа, что также повысит выразительную мощность моделирования при помощи графов.

Во многих междисциплинарных прикладных задачах при исследовании сложных динамических систем возникает потребность в модельном отображении еще одного очень важного качества систем – отображении “части и целого”. Особенно важно такое расширение выразительной мощности модели для моделирования социальных явлений, процессов и структур.

Развитие модели графов в этом направлении принесёт в моделирование систем совершенно новое и важное качество – разделение пространства на две противоположных области относительно субъекта — “внутреннее пространство” и “внешнее пространство”. В свою очередь, такое разделение пространств приводит к необходимости раскрытия понятия границы между ними.

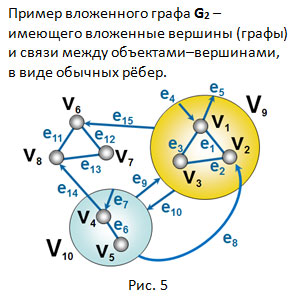
На Рис.5 показан пример вложенного графа, у которого две вершины — v₉ и v₁₀ имеют вложение. Кроме обычных связей-рёбер типа e₁₁ или e₁, например, показаны иерархические связи: e₉ = (v_10, v₁₁) – ребро между вершинами степени 2, e₈ = (v_10, v₂) – ребро между вершиной степени 2 и вложенной вершиной степени 1; e₁₄ = (v_4, v₈) – ребро между вложенной вершиной степени 1 и простой вершиной степени 1; e₅ = (v_1, v₉) – ребро между вложенной вершиной степени 1 и вершиной степени 2, в которую начало этого ребра v₁ само вложено; и наоборот e₄ = (v_9, v₁) – ребро между вершиной степени 2, в которую вложен конец этого ребра — v₁; e₁₅ = (v_9, v₆) – ребро между вершиной степени 2 и простой вершиной степени 1.

Если в системе присутствуют сложные объекты-вершины, содержащие в своём составе другие объекты в количестве вложения q≥1, то модель графа, показывающего такую структуру связей, называется вложенным графом степени q.

Определение. Вложенный граф степени q – это граф G_q = (V, E), который состоит из конечного множества вершин V = {v_1, v_2, v_{3, …} v_n} и конечного множества рёбер между ними E = {e_1, e_2, e_{3, …} e_m}.

Следует отметить, что для вложенных вершин имеется внутренняя и внешняя области пространства системы. Это поможет по-новому взглянуть на парадигму мембраны, если её представить не просто математической плоской поверхностью, а в виде особой сложной динамической системой, обладающей своей структурой, функциями и осуществляющую свои внутренние процессы, в том числе на информационном уровне.

Вложенные гиперграфы. При построении сложных структур возникает необходимость отслеживать сложные связи (а не только бинарные) с одновременным выделением иерархических структур и их связей, включая одноуровневые, межуровневые, а также смешанные. Такие возможности даёт конструкция вложенного гиперграфа. К сожалению, формальное описание таких сложных графовых конструкций на языке теории множеств достаточно громоздко и ненаглядно. Необходимо искать иные способы формализации математического описания. Но к этому можно привыкнуть. Главное – это включение в практику и развитие новых опорных образов мышления, возникающих с применением геометрических и иных структурных и пространственных парадигм в исследовательский арсенал мышления. В определённом смысле мыслительной базы опорных образов даёт явное усиление интеллекта.

Определение. Вложенный гиперграф степеней (p, q) – это граф G^p_q = (V,E), который состоит из конечного множества простых и вложенных вершин, а также конечного множества связей в виде простых рёбер и гипер-рёбер между ними.

При этом связи (гипер-рёбра) вложенного гиперграфа G^p_q могут связывать до p≥3 вершин одновременно (при p=2 это рёбра между двумя вершинами обычного графа). Также в системе G^p_q присутствуют сложные объекты-вершины, содержащие в своём составе другие объекты в количестве вложения q≥2 (при q=1 это вершины обычного графа без вложенности). Кроме обычных гипер-рёбер между объектами одного уровня могут присутствовать иерархические связи.

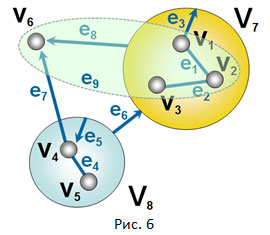
На Рис.6 показан пример вложенного гиперграфа G⁴₂, имеющего вложенные вершины (внутри имеются графы) второй степени – это две вершины v₇ и v₈. Также имеется связь четвёртой степени сложности – гипер-ребро e₉, охватывающая четыре вершины – v_1, v_2, v_3, v₆ (показана пунктирным овалом зелёного цвета). Вложенные гиперграфы – это достаточно сложные конструкции, допускающие множество непривычных связей. Например, если включить в гипер-ребро e₉ еще одну вершину v₈, имеющую вложение (вершины v₇ и v₈), то получается достаточно непривычный объект, образ которого трудно на первых порах удерживать в сознании. Но и это не предел. Кстати, к категории сложных систем этот непривычный объект не относится (см. параграф “Проблемы изучения сложных систем и математические вызовы”).

Визуальные образы графов очень удобны. К сожалению, математические описания графов очень неудобны и ненаглядны. Налицо высокая перегрузка математическим формализмом, что создаёт серьёзные препятствия для их применения в прикладных целях. Однако, постараемся преодолеть это препятствие – наградой будут новые образы и понимание.

Сети Петри, расширения и их опорные образы мышления

Сети Петри это математический аппарат, разработанный немецким математиком и исследователем в области информатики Карлом Петри в 1962 году для моделирования событий в виде параллельных и распределённых компьютерных вычислений. Всплеск интереса к сетям Петри возник ещё в 80-х годах. С тех пор в информатике и компьютерных кругах знание сетей Петри рекомендуется специалистам как атрибут информационной грамотности. Но в широких кругах исследователей понимания возможностей сетей Петри так и не возникло.

Определим для начала конечную сеть Петри [8], чтобы с её помощью определить нужные нам расширения сетей Петри. Сеть Петри представляет собой двудольный ориентированный мультиграф, состоящий из вершин двух типов – позиций и переходов, соединённых между собой ориентированными дугами. Вершины одного типа не могут быть соединены непосредственно дугами. Дуги могут соединять только позиции с переходами или наоборот переходы с позициями. Кстати, дуги могут быть кратными (однонаправленными) и встречными. Но дуги в форме петель недопустимы.

В позициях могут размещаться маркеры. Иногда их называют метками, фишками, эстафетами (англ. token). Маркеры способны как бы перемещаться по сети из позиции в позицию, но только посредством переходов. В этом состоит различие позиций и переходов. Позиция, из которой идет дуга в переход, называется для него входной. И наоборот, если из перехода идет дуга в позицию, то она называется выходной позицией.

Срабатывание перехода называют событием в сети. В процессе срабатывания перехода маркеры из входных позиций этого перехода перемещаются в его выходные позиции. Причём, нужно строго учитывать кратность дуг: сколько входных дуг, столько и забирается маркеров из входных позиций; сколько выходных дуг, столько же отдается маркеров в выходные позиции. Так что количественный закон сохранения маркеров здесь не работает. Должно быть соответствие количества входных дуг с количеством маркеров, забираемых из входных позиций. Аналогичное правило для новых маркеров. Сколько выходных дуг, соответственно столько же будет произведено маркеров в их выходных позициях. События происходят мгновенно и асинхронно (разновременно). Это отличается от нашего привычного восприятия времени. Для исполнения события в конкретном переходе необходимо исполнение условий, указанных выше: для каждой входной дуги необходим один маркер во входной позиции, который из неё изымается. А если хотя бы для одной дуги не хватит одного маркера, то переход не сможет сработать, а данное событие вообще не сможет произойти. А все маркеры остаются на месте – нет события.

Структура сети Петри есть мультиграф, так как он допускает существование кратных дуг из позиции в переход и/или наоборот. Так как дуги являются направленными, то это ориентированный мультиграф. Напомним, вершины графа можно разделить на два множества (позиции и переходы) таким образом, что каждая дуга будет направлена от элемента одного множества (позиций или переходов) к элементу другого множества (переходов или позиций); следовательно, структура такого графа является двудольным ориентированным мультиграфом.

Распределение маркеров в позициях сети называется её разметкой. С одной стороны, поведение сети зависит от начальной разметки сети, с другой стороны – от выбора очерёдности срабатывания переходов в различных состояниях разметки сети. Для описания сети необходимо указать её структуру и начальную маркировку. А вот для описания процессов необходимо понимать, что существует поле путей развития (все возможные варианты её доступных разметок). В поле путей развития существуют траектории – варианты логических последовательностей маркировок, соответствующих последовательностям срабатывания переходов.

На Рис. 7 показан пример простой сети Петри в виде трёх вариантов её разметки (A, B, C). Причём, из состояния A сеть может перейти в состояние B, либо в состояние C.

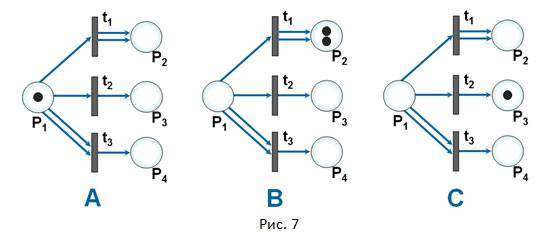
Разберём подробно на примере Рис. 7, как работает сеть Петри. Сеть содержит: четыре позиции и три перехода; начальную разметку A с одним маркером. Для этой сети имеется два варианта выбора её событийного процесса (разметки B или C) и возможность совершить всего один такт действия в сторону B или C. Вариант разметки А показывает начальное состояние: позиция P₁ содержит только один маркер. P₁ является входной позицией для трёх переходов (t₁, t₂, t₃). Но сработать могут только два  перехода t₁, t₂. Переход t₃ не может сработать – для двух его входных дуг имеется всего один маркер.

Вариант B показывает ситуацию в сети после срабатывания перехода t₁, а вариант C – ситуацию после срабатывания перехода t₂. В варианте B в соответствии с правилами в позиции P₂ появляются два маркера, так как из перехода t₁ в позицию P₂ идут две выходные дуги. В варианте С в позиции P_з появляется один маркер.

На Рис. 8 показан очень важный пример сети Петри, раскрывающий, как происходит распараллеливание в сети на множество процессов с их последующей синхронизацией. Здесь ключевыми являются конструкции parbegin и parend (сегменты A_b и A_e). Пример показывает, как происходит распараллеливание в сегменте A_b на три процесса, а затем их синхронизация в сегменте A_e. Но по аналогии можно представить любое количество параллельных процессов, а принцип действия будет такой же. В сетях Петри смысловой образ маркера ассоциируется с образом точки процесса: то есть маркер это текущий момент времени в процессе, его “горячая точка”, а траектория в потенциальном поле путей развития это один из вариантов, по которому идет сам процесс (аналогично тому, как было показано на Рис. 7).

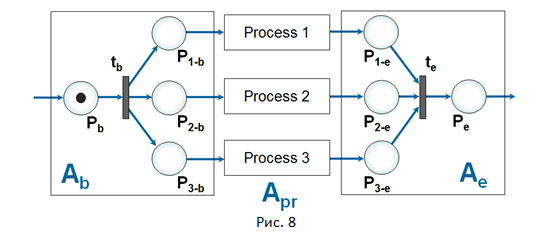
Дадим небольшое пояснение к Рис. 8. В сегменте parbegin A_b сигнальный маркер из позиции P_b переходит посредством перехода t_b в три позиции P_1-b, P_2-b, P_3-b (в каждой по своему маркеру) в соответствие со структурой сети. Это показывает, что изначальный один локальный процесс превратился в три реальных локальных процесса в сегменте A_pr. В сегменте parend A_e три позиции P_1-e, P_2-e, P_3-e ожидают свои маркеры из соответствующих процессов сегмента A_pr. Причём это контролирует переход t_e. Он сможет сработать только тогда, когда все три эти процесса завершатся. Но если хотя бы один из этих процессов не завершится, то переходу t_e придётся ждать. Как только три позиции P_1-e, P_2-e, P_3-e получат свои маркеры, переход t_e сработает, забирая их, и создаст сигнальный маркер в позиции P_e, что символизирует завершение синхронизации.