Введение
В последние годы теория сложных сетей привлекает широкое внимание исследователей как новый эффективный инструмент изучения сложных систем самой разнообразной природы: от биологических, когнитивных и социальных до информационно-технологических систем [1-5,7,8].
Заимствовав из классической теории графов многие важные понятия и методы, современная теория сложных сетей базируется на обнаруженных эмпирическим путем универсальных свойствах реальных сетей (Интернет, WWW, профессиональные сети, сети друзей и знакомых, сети метаболических реакций и белковых взаимодействий в живой клетке т т.д.) и, прежде всего, на общем для всех перечисленных и многих других реальных сетей степенном законе распределения узлов по числу связей. Сети, характеризующиеся степенным законом распределения узлов по числу связей, получили название безмасштабных сетей (scale free networks) или сложных сетей (complex networks). Степенной закон распределения узлов по числу связей означает, что сложные сети состоят из большого числа узлов с малым числом связей и небольшого числа узлов с большим числом связей — хабов (от английского hub – концентратор, накопитель), которые во многом и определяют свойства сложных сетей. Для изучения свойств безмасштабных сетей широко используются методы статистической физики, прежде всего теории критических явлений (фазовые переходы, самоорганизованная критичность, синхронизация, перколяция).
Среди огромного числа публикаций приложений теории сложных сетей в исследовании реальных сетевых структур имеется всего лишь несколько статей, посвященных изучению сетей городского общественного транспорта [9-11,16,17]. В работах [16,17] проанализированы статистические свойства систем общественного транспорта соответственно 22 городов Польши и трёх городов Китая. Наиболее полное и обстоятельное исследование по данной проблеме содержится в работе [11]. В этой работе изучены свойства объединенных сетей общественного транспорта для 14 мегаполисов мира в модельных представлениях теории сложных сетей, проведен анализ локальных и глобальных характеристик этих сетей, исследованы вопросы надежности и уязвимости, а также проблемы оптимизации транспортных сетей.
В России изучение систем общественного транспорта на основе теории сложных сетей проводилось только для метрополитена города Москвы [4, 5]. Настоящая работа посвящена исследованию основных свойств автобусной и троллейбусной сетей города Москвы, а также всей дорожной инфраструктуры мегаполиса.
Сетевые пространства: L- пространство, P — пространство и С- пространство
Для изучения транспортных сетей города Москвы будем использовать известные стандартные топологические представления теории сложных сетей, а именно, L- пространство, P — пространство и С- пространство (L-space, P-space и С-space в англоязычной литературе).
L — пространство – естественное представление транспортной сети, где каждой остановке соответствует узел. При этом между двумя узлами имеется связь, если хотя бы один из транспортных маршрутов проходит через соответствующие остановки последовательно. Таким образом, в L- пространстве связями между узлами являются маршруты, последовательно соединяющие эти узлы. В L- пространстве введена длина пути (связи) между двумя узлами, которая определяется количеством соединяемых связью узлов плюс один. Степень узла – количество различных направлений, выходящих из узла. Конструкция L — пространство используется при анализе транспортных сетей в работах [11,16].
В P — пространстве узлами также считаются остановки. Два узла связаны, если хотя бы один из транспортных маршрутов проходит через соответствующие остановки (не обязательно последовательно). Таким образом, связи между узлами в P — пространстве — это проходящие через них транспортные маршруты. Узлы, которые имеют более одной связи, называются пересадочными узлами. Длина пути (связи) между двумя узлами в P — пространстве – это количество пересадочных узлов на связи плюс один, а степень узла – количество узлов со связями без пересадочных узлов. Иллюстрация сетевых пространств, L -пространства и P – пространства, представлена на Рисунке 1.
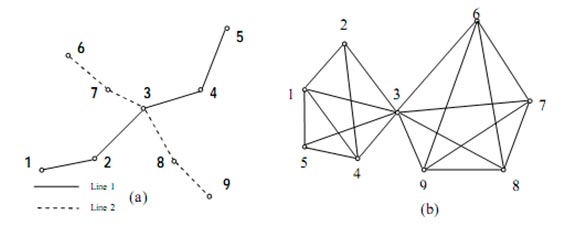
Рисунок 1. Иллюстрация пространств (a) L — пространство, (b) P — пространство
В C — пространстве узлами являются маршруты, связями – остановки. Два узла называются связанными, если они имеют общие связи (остановки). В C — пространстве удобно исследовать свойства маршрутов, например, выявлять наиболее топологически загруженные маршруты. Примеры успешного использования C — пространства содержатся в работе [11].
Некоторые понятия теории сложных сетей
В теории сложных сетей используются два основных типа параметров сети – локальные и нелокальные характеристики сети.
Локальные характеристики сложных сетей – степень узла (degreecentrality) ([1,5]) и коэффициенты Ki кластеризации i –того узла [1],
![]()
Здесь ti - число треугольников – циклов длины 3, прикрепленных к узлу с номером i, ni – максимально возможное число треугольников в i – том узле, ni = qi(qi - 1) / 2, где qi = qi(ti) – количество близких к i –тому узлу узлов с числом связей.
Таким образом,
![]() При этом Ki (ti) = 0, если связи между узлами отсутствуют.
При этом Ki (ti) = 0, если связи между узлами отсутствуют.
Кластеризация всей сети K определяется отношением
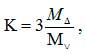
где MΔ – число треугольников в сети, а Mv– число «вилок», где «вилка» означает узел и две его связи (ребра), Mv = Σi ni.
Рассматривается также среднее значение кластеризации по всем узлам:
![]() где N – число узлов сети.
где N – число узлов сети.
Таким образом, кластеризация характеризует статистику циклов длины 3 (треугольников) в сети. Большинство реальных сетей обладают высокой кластеризацией, на порядки превышающей кластеризацию классических пуассоновских случайных сетей.
Нелокальные характеристики сложных сетей представлены коэффициентом ассортативности r сети, параметрами betweenness centrality узла и closeness centrality узла ([1, 5]).
Коэффициент ассортативности r сети характеризует степень корреляции узлов сети между собой и представлен статистической величиной – коэффициентом Пирсона ([5]).
Отрицательная ассортативность свойственна технологическим и биологическим сетям [7], в социальных же сетях имеет место положительная ассортативность, что является следствием того, что в них действует принцип: «подобное соединяется с подобным» [12].
Параметр betweenness centrality узла характеризует топологическую загруженность сети в ее узлах и определяется долей проходящих через узел кратчайших путей сети к общему числу кратчайших путей между всеми парами узлов сети. Аналитическое выражение для параметра betweenness centrality узла представлено, например, в работе [5].
Показатель closeness centrality Ci узла с номером i характеризует среднюю близость к данному узлу всех остальных узлов сети и определяется формулой
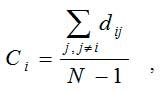
где N — общее число узлов, dij- число кратчайших маршрутов между узлами с номерами i и j.
Исходные данные
В работе для получения исходных данных о системе автобусного и троллейбусного сообщений в городе Москве использовались открытые в Интернете для общего пользования сайты «Московский автобус» (http://bus.ruz.net/) и «Московский троллейбус» (http://trolley.ruz.net/). Кроме того, выбор этих источников информации был предопределен еще и следующими причинами. Во-первых, здесь имеется вся необходимая информация. Во-вторых, эта информация надежна, так как предоставлена сайтам одним из филиалов ГУП «Мосгортранс». В-третьих, информация поддерживается актуальной (регулярно обновляется). И, наконец, эти сайты очень схожи по своей структуре, а значит, программа для извлечения данных с одного из них легко модифицируется для работы с другим сайтом. На вкладке «Маршруты» сайта (например, сайт автобусов) имеется список всех маршрутов в виде ссылок. Для каждого из маршрутов имеется страница с полным его описанием: номером, начальным и конечным пунктами, а также полным списком остановок по порядку при прямом и обратном следовании (опять же в виде ссылок). Для каждой остановки, в свою очередь, имеется страница, где содержатся: название остановки, ссылка на «Яндекс.Карты» (по которой при необходимости можно определить её координаты), список всех маршрутов, которые здесь останавливаются, и список ближайших остановок (что, как будет показано далее, также немаловажно).
Предположения при построении сети
При построении сети учитывался тот факт, что некоторые остановки находятся вблизи друг от друга (на расстоянии «шаговой доступности»). Например, такая ситуация нередко встречается в центре города, у остановок метро и на пересечении улиц (остановки «за углом»). Для пассажира такие остановки фактически являются одной остановкой. В связи с этим было принято решение в пространствах L и P группу близлежащих остановок считать одним узлом, а в С — пространстве отождествлять маршруты, связанные близкими узлами (близлежащими остановками).
Основные результаты
Были построены транспортные сети автобусов и троллейбусов города Москвы в трех основных сетевых пространствах.
L -пространство
Распределение степеней узлов
На Рисунке 2 изображены графики распределения степеней узлов для автобусной и троллейбусной сетей города Москвы в логарифмическом масштабе.
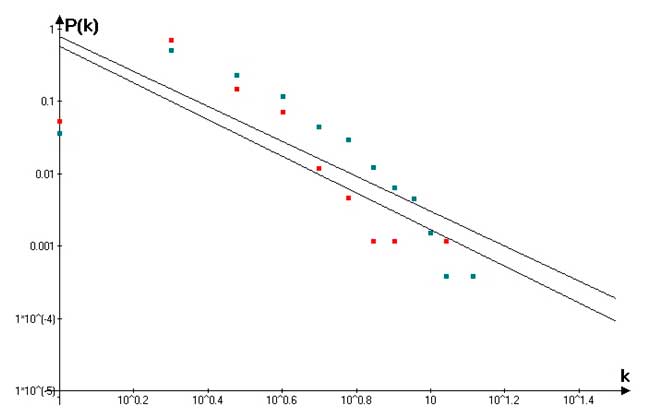
Рисунок 2. Распределение степеней узлов в L — пространстве для автобусной (синий цвет) и троллейбусной (красный цвет) сетей города Москвы
Распределение степеней узлов в L — пространстве подчиняется степенному закону: P(q) ∝ q-γ. Следовательно, как и большинство реальных сетей, данные сети являются безмасштабными. Показатели степени γ составляют 2.4 и 2.5 для автобусной и троллейбусной сети, соответственно. Этот результат согласуется с известными исследованиями, поскольку для сложных сетей это значение обычно лежит в пределах 2 < γ ≤ 3.
Таким образом, для сетей наземного общественного транспорта Москвы, как и для всех безмасштабных сетей, характерно наличие большого числа узлов с малым числом связей и небольшого числа хабов. Список хабов для сети автобусов приведен в Таблице 2. Наиболее вероятным значением степени узла, как следует из графика, является 2. То есть, наибольшее количество остановок имеют по две соседние остановки. Количество узлов с одной связью не велико. Им соответствуют конечные остановки маршрутов.
Распределение узлов по числу маршрутов, обслуживающих остановки.
Для L — пространства было рассмотрено количество автобусов (и троллейбусов), обслуживающих каждую остановку. Распределение узлов по этому параметру также является степенным. Показатель степени для автобусов – около 2.3, для троллейбусов – около 2.5. Соответствующие графики изображены на Рисунке 3. Схожие результаты были получены для сетей автобусов трех китайских городов [17]. Объяснить подобную закономерность можно следующим образом. На окраинах города находится много остановок, на которых останавливаются небольшое количество автобусов (троллейбусов) по сравнению с центром города. А в центре города – наоборот: небольшое количество остановок обслуживается большим числом маршрутов.
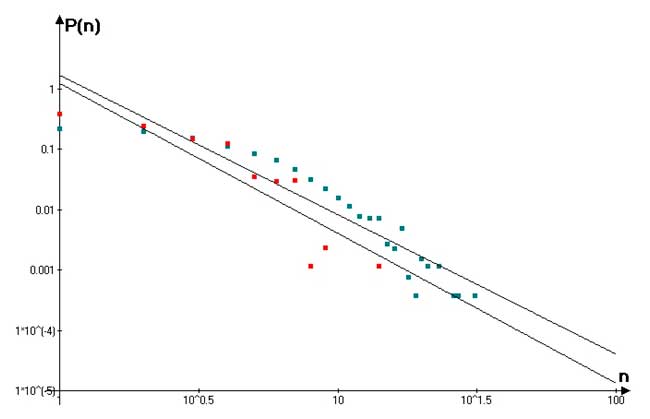
Рисунок 3. Распределение остановок по числу обслуживающих их маршрутов.
Автобусы обозначены синим цветом, троллейбусы – красным цветом.
Основные результаты исследования сетей автобусов и троллейбусов в L -пространстве представлены в Таблице 1.
Таблица 1. Основные результаты исследования автобусных и троллейбусных сетей в L- пространстве
|
Сеть автобусов |
Сеть троллейбусов |
|
|
Количество узлов |
2631 |
853 |
|
Количество связей |
3722 |
988 |
|
Средняя кластеризация |
0,13 |
0,07 |
|
Средняя кратчайшая длина пути |
25,5 |
27,6 |
|
Ассортативность |
0,083 |
0,107 |
Таким образом, в L -пространстве исследуемые сети имеют большую среднюю длину пути и низкую кластеризацию. В среднем, пассажиру в автобусной и троллейбусной сети, чтобы добраться от одной остановки до другой, требуется проехать около 25 и 28 остановок, соответственно. Для сравнения в автобусных сетях Пекина и Шанхая средняя длина пути измеряется, соответственно, величинами 12.56 и 7.13 [17]. При этом также отметим, что обе рассматриваемые нами сети обладают положительной ассортативностью. Визуализация сетей представлена на Рисунках 4 и 5.
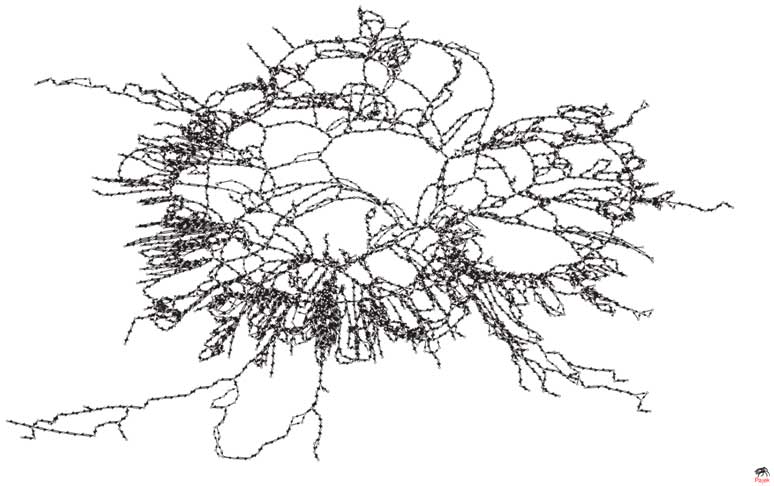
Рисунок 4. Сеть автобусов города Москвы в естественном представлении (L- пространство)
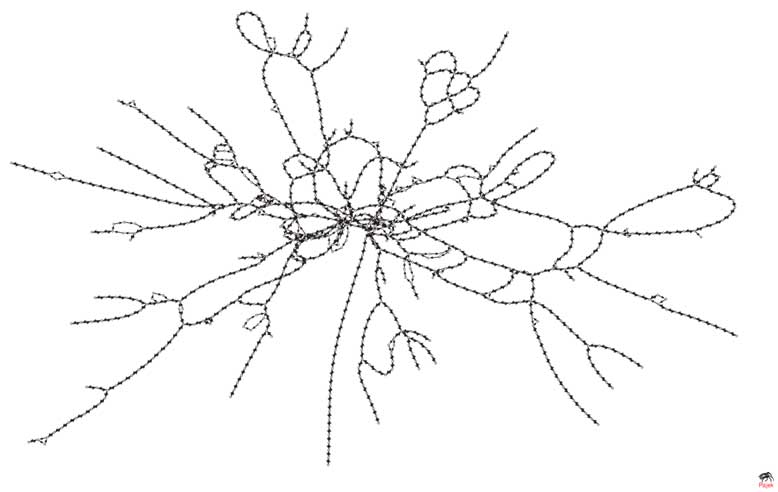
Рисунок 5. Сеть троллейбусов города Москвы в естественном представлении (L -пространство)
Наиболее важные остановки
Список узлов с наибольшими значениями степени узлов и коэффициентов betweenness centrality и closeness centrality представляет наиболее важные остановки в автобусной и троллейбусной сети города Москвы.
Данные о значимости остановок в сети автобусов представлены в Таблицах 2-4. Узлы с наибольшими значениями сетевых параметров соответствуют остановкам у вокзалов (Белорусского, Рижского, Киевского), метро (Чеховская, Динамо, Молодежная, Домодедовская) и остановкам вблизи других важных инфраструктурных объектов (МГУ, стадион “Динамо”, площади, кинотеатры, торговые комплексы).
Таблица 2. Список 5 узлов автобусной сети в L- пространстве c наибольшей степенью
| Узел (группа близких остановок) |
Степень узла |
| ‘ДСК-3′, ‘Домостроительная улица’ |
13 |
| ‘Теплостанский проезд’, ‘Зона отдыха’ |
11 |
| ‘Торговый комплекс’, ‘Платформа Лианозово’, ‘Псковская улица, 2′, ‘Керамический проезд’ |
10 |
| ‘Стадион юных пионеров’, ‘Стадион «Динамо»‘, ‘Метро «Динамо» ‘, ’1-й Боткинский проезд’ |
10 |
| ‘Кинотеатр «Брест»‘, ‘Метро «Молодёжная» ‘ |
10 |
| ‘Метро «Домодедовская» ‘, ‘Ореховый бульвар, 21′, ‘Киноконцертный комплекс «Авангард» ‘, ‘Торговый комплекс «Облака»‘ |
10 |
Таблица 3. Список 5 узлов автобусной сети в L- пространстве c наибольшими значениями betweenness centrality
| Узел (группа близких остановок) |
Betweenness centrality |
| ‘Стадион юных пионеров’, ‘Стадион «Динамо» ‘, ‘Метро «Динамо» ‘, ’1-й Боткинский проезд’ |
0.288 |
| ‘Белорусский вокзал’, ‘Метро «Белорусская» ‘, ’2-й Лесной переулок’, ’3-я улица Ямского Поля’, ’2-й часовой завод’ |
0.222 |
| ‘Площадь Индиры Ганди’, ‘МГУ’ |
0.199 |
| ‘Рижский вокзал’ |
0.187 |
| ‘Пушкинская площадь’, ‘Тверская улица’, ‘Глазная больница’, ‘Белорусский вокзал’, ‘Триумфальная площадь’, ‘Тверской бульвар’, ‘Улица Гашека’, ‘Петровские ворота — Музей современного искусства’, ‘Улица Юлиуса Фучика’, ‘Большая Грузинская улица’, ‘Метро «Чеховская» ‘ |
0.184 |
Таблица 4. Список узлов автобусной сети в L- пространстве c наибольшими значениями closeness centrality
| Узел (группа близких остановок) |
Closeness centrality |
| ‘Арбатские ворота — Музей Востока’, ‘Никитские ворота’ |
0.56 |
| ‘Пушкинская площадь’, ‘Тверская улица’, ‘Глазная больница’, ‘Белорусский вокзал’, ‘Триумфальная площадь’, ‘Тверской бульвар’, ‘Улица Гашека’, ‘Петровские ворота — Музей современного искусства’, ‘Улица Юлиуса Фучика’, ‘Большая Грузинская улица’, ‘Метро «Чеховская» ‘ |
0.55 |
| ‘Скарятинский переулок’, ‘Ножовый переулок’, ‘Кудринская площадь’ |
0.55 |
| ‘Белорусский вокзал’, ‘Метро «Белорусская» ‘, ’2-й Лесной переулок’, ’3-я улица Ямского Поля’, ’2-й часовой завод’ |
0.55 |
| ‘Площадь Индиры Ганди’, ‘МГУ’ |
0.55 |
Высокие значения степени и коэффициентов betweenness centrality и closeness centrality демонстрируют узлы, соответствующие остановкам у стадиона “Динамо”, МГУ, Белорусского, Рижского и Киевского вокзалов. Эти остановки являются наиболее важными в транспортной сети автобусов города Москвы.
Наиболее важным для транспортных сетей показателем является коэффициент betweenness centrality, так как он характеризует количество кратчайших путей в сети, проходящих через данный узел. Таким образом, остановки у стадиона “Динамо” и Белорусского вокзала являются наиболее топологически загруженными (см. Таблицу 4).
P -пространство
Основные результаты
Степенью узла в P -пространстве является количество остановок, в которые можно попасть из данного узла (остановки) без пересадок. Было установлено, что распределение степени узла в P -пространстве является экспоненциальным:
P(k) = Ae-αk
Соответствующий график изображен на Рисунке 6:
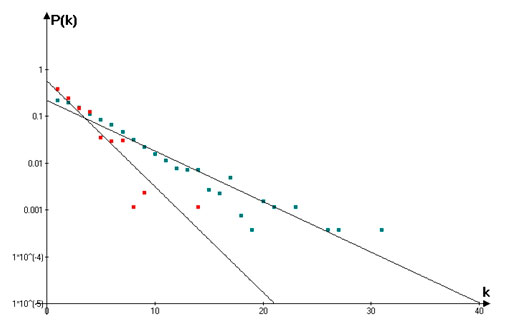
Рисунок 6. Распределение степеней узлов в P -пространстве
(автобусы – синий цвет, троллейбусы – красный цвет)
Основные результаты для P -пространства представлены в Таблице 5. Так как в этом представлении каждый маршрут формирует полный подграф, количество связей значительно больше, чем в L -пространстве. Также по этой причине получилась большая величина кластеризации и малая длина пути. Средняя длина пути в P - пространстве равна среднему количеству пересадок, которое необходимо сделать при движении по кратчайшему маршруту между произвольными двумя остановками. Для сети автобусов среднее количество пересадок равно 3.5, а для сети троллейбусов равно 2.5.
Таблица 5. Основные результаты для сетей автобусов и троллейбусов в P -пространстве
|
Сеть автобусов |
Сеть троллейбусов |
|
|
Количество узлов |
2631 |
853 |
|
Количество связей |
59587 |
15100 |
|
Средняя кластеризация |
0.72 |
0.83 |
|
Средняя кратчайшая длина пути |
4.5 |
3.5 |
|
Ассортативность |
0.058 |
0.226 |
|
Средняя степень узла |
45.3 |
35.4 |
С — пространство
В отличие от пространств L и P, узлами в С — пространстве являются не остановки, а
маршруты. По этой причине С — пространство является удобным для исследования свойств транспортных маршрутов. На Рисунках 7 и 8 представлены маршрутные сети для троллейбусов и автобусов.
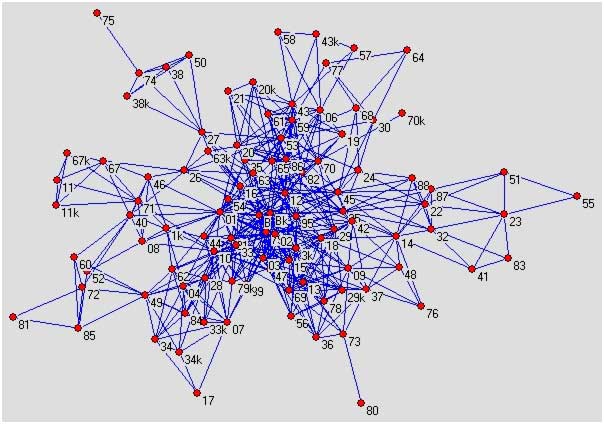
Рисунок 7. Сеть троллейбусных маршрутов (С -пространство)
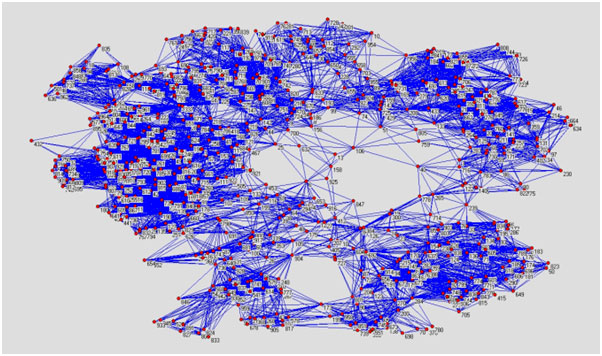
Рисунок 8. Сеть автобусных маршрутов (С -пространство), которая содержит восемь кластеров (сообществ) соответствующих восьми из девяти административных округов Москвы (за исключением ЦАО)
Основные результаты
Распределение степеней узлов
Функции распределения степеней узлов для автобусных и троллейбусных маршрутов проявляют схожие и довольно неожиданные свойства. Для обеих сетей в С — пространстве функция распределения узлов по количеству связей имеет вид:
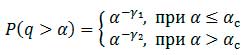
Таким образом, функция распределения состоит из двух степенных функций с разными значениями показателя степени при малых и при больших значениях параметра α. Полученное распределение согласуется с результатами работы [17], где также наблюдалось подобное распределение для автобусных сетей. Для сети автобусов γ1 ≈ 3.27, γ2 ≈ 0.19; для сети троллейбусов γ1 ≈ 1.7, γ2 ≈ 0.31. Соответствующие графики изображены на Рисунке 9.

Рисунок 9. Распределение степеней узлов в С-пространстве
(автобусы – синий цвет, троллейбусы – красный цвет)
Основные результаты для сетей в С-пространстве сведены в Таблицу 6.
Для этого представления также характерна высокая кластеризация. Это означает, если два маршрута пересекают третий, то, скорее всего, они и сами пересекаются. Средняя длина пути в С-пространстве означает среднее количество пересадок, необходимое, чтобы пересесть с одного маршрута на другой. Для троллейбусных и автобусных маршрутов средняя длина пути в С-пространстве равна приблизительно 3 и 4, соответственно. Коэффициенты ассортативности для обеих сетей являются достаточно большими положительными величинами.
Таким образом, во всех трех сетевых пространствах ассортативность рассмотренных транспортных структур является положительной. Это означает, что сети автобусного и троллейбусного транспорта города Москвы, по крайней мере, по характеру корреляции узлов схожи с социальными сетями. Выявленное свойство предполагает необходимость дальнейших исследований сетей наземного транспорта в этом направлении.
Таблица 6. Основные результаты для сетей автобусов и троллейбусов в С-пространстве
|
Сеть автобусов |
Сеть троллейбусов |
|
|
Количество узлов |
645 |
102 |
|
Количество связей |
8348 |
518 |
|
Средняя кластеризация |
0.69 |
0.64 |
|
Средняя кратчайшая длина пути |
4.1 |
2.9 |
|
Ассортативность |
0.313 |
0.287 |
|
Средняя степень узла |
25.9 |
10.16 |
В Таблице 6 присутствует среднее значение степени узла. Стоит отметить, что для автобусных маршрутов этот показатель существенно больше. Следовательно, автобусные маршруты пересекаются значительно чаще троллейбусных маршрутов.
Наиболее важные маршруты
В Таблице 7 приведены хабы в С — пространстве, то есть маршруты пересекающие наибольшее количество других маршрутов. В Таблице 8 представлены маршруты с наибольшими значениями betweenness centrality, то есть наиболее топологически загруженные маршруты. И, наконец, в Таблице 9 собраны маршруты в среднем наиболее близкие ко всем остальным.
По всем трем показателям маршрут № 816 (Метро «Калужская» — ВКНЦ) является одним из самых важных и загруженных ых важных из периям важности маршрут №ным маршруты.других маршрутов. схожие и довольно интересные свойства.ливать .
Таблица 7. Список узлов автобусной сети c наибольшей степенью в С-пространстве
|
№ автобуса |
Маршрут следования |
Степень узла |
|
688 |
Озёрная улица — Крылатское |
84 |
|
37 |
Метро «Красногвардейская» — Метро «Тёплый Стан» |
70 |
|
196 |
Метро «Юго-Западная» — Калужская площадь |
70 |
|
699 |
Севастопольский проспект — Станция Очаково |
65 |
|
337 |
Метро «Красногвардейская» — Метро «Тёплый Стан» |
64 |
Таблица 8. Список узлов автобусной сети c наибольшими значениями betweenness centrality в С-пространстве
|
№ автобуса |
Маршрут следования |
Betweenness centrality |
|
99 |
138-й квартал Выхина — Автозаводский мост (по выходным — Метро «Автозаводская») |
0.089 |
|
816 |
Метро «Калужская» — ВКНЦ |
0.075 |
|
239 |
ВДНХ (южная) — Метро «Сокольники» |
0.068 |
|
12 |
Метро «Тимирязевская» — 2-й Красногвардейский проезд |
0.064 |
|
798 |
Метро «Щукинская» — ВКНЦ |
0.062 |
Таблица 9. Список узлов автобусной сети c наибольшими значениями closeness centrality в С-пространстве
|
№ автобуса |
Маршрут следования |
Closeness centrality |
|
6 |
Силикатный завод — Павелецкий вокзал |
0.311 |
|
130 |
Метро «Филёвский парк» (в часы «пик» — Лес) — 23-й квартал Новых Черёмушек |
0.309 |
|
44 |
Метро «Профсоюзная» — Метро «Кожуховская» |
0.308 |
|
816 |
Метро «Калужская» — ВКНЦ |
0.307 |
|
142 |
Метро «Кожуховская» — Метро «Академическая» |
0.307 |
Сообщества автобусных маршрутов
Для сети автобусных маршрутов города Москвы, за исключением Зеленоградского территориального образования, в представлении С-пространства был применен алгоритм разбиения сети на сообщества [6,13]. Рисунок 8 иллюстрирует разбиение автобусной сети Москвы на отдельные сообщества – кластеры. Оказалось, что в данной сети имеется 8 сообществ, причем маршруты одного сообщества в основном проходят внутри одного и того же округа Москвы. Следовательно, структура разбиения сети автобусных маршрутов на сообщества отражает административное деление города. Таким образом, автобусные маршруты, проходящие через один административный округов более связаны, чем маршруты между соседними округами. Исключением является лишь Центральный административный округ, который содержит лишь незначительное число полных автобусных маршрутов, и поэтому ему не может быть сопоставлено никакое сообщество маршрутов.
Дорожная сеть Москвы
Все автомобильные потоки в городе, включая маршруты наземного общественного транспорта, осуществляются в рамках его дорожной инфраструктуры. Поэтому, для понимания природы всех транспортных проблем любого города необходимо знание сетевых характеристик его дорожной инфраструктуры. В [14,15] опубликованы результаты таких исследований для некоторых крупных городов Европы и США. В России такие исследования до настоящего времени не проводились.
В данной работе дорожная структура города Москвы представляется в виде сети, в котором узлами являются перекрестки улиц, а ребрами являются части улиц соединяющих два узла. В текстовом файле был создан список ребер, где каждая строка содержит три числа. Первые два числа являются номерами узлов, между которыми проведено данное ребро, третье число принимает значение 1 или 2 , в зависимости от того является ли движение в данном отрезке улицы односторонним или двусторонним.
Кроме того, в данной работе был построен граф и рассчитаны основные показатели для дорожной сети всей Москвы. Для этого были использованы исходные данные задачи из Яндекс математика 2010. Эти данные позволяют рассчитать основные сетевые параметры без восстановления географического местоположения узлов в связи с отсутствием в них названий улиц и координат. В таблице 10 приведены основные характеристики для дорожной сети Москвы.
При построении графа длина ребер (отрезков дорог между перекрестками) принималась за 1 и не учитывалась многополосность дорог. В таком допущении путь между двумя точками определяется количеством пройденных перекрестков на пути от одной точки до другой.
Дорожная инфраструктура города Москвы как безмасштабная сеть
На Рисунке 10 представлен в логарифмическом масштабе график распределения узлов по количеству связей для дорожной инфраструктуры города Москвы. В соответствии с графиком дорожная сеть Москвы является с достаточной степенью точности безмасштабной сетью с показателем γ = 2.064 .
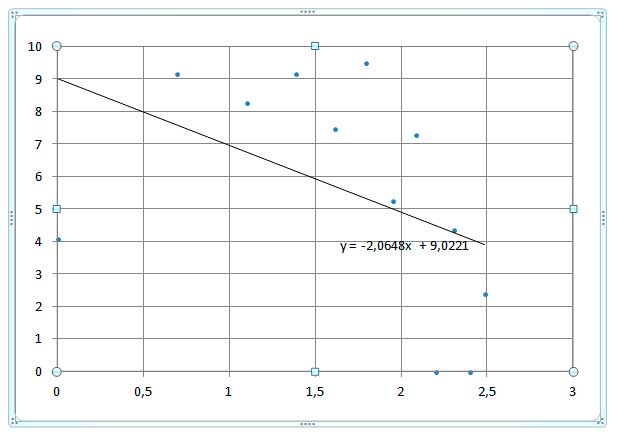
Рисунок 10. График распределения узлов по числу связей для дорожной сети города Москвы
