Баяковский Юрий Матвеевич – кандидат физико-математических наук, заведующий лабораторией компьютерной графики и мультимедиа при факультете ВМиК МГУ,
Галактионов Владимир Александрович — кандидат физико-математических наук, заведующий отделом машинной графики ИПМ им.М.В.Келдыша РАН

В этой лекции дан краткий очерк ранних работ по машинной графике, выполненных в ИПМ им. М.В.Келдыша РАН, обозначены основные направления исследований и разработок, проведенных отделом машинной графики Института за последнее десятилетие. В качестве главного направления было выбрано физически аккуратное моделирование распространения света в оптически сложных средах. Предложены методы физически аккуратного моделирования и визуализации оптически сложных материалов (современные автомобильные краски, ткани) в условиях искусственного и естественного освещения. Рассмотрены некоторые аспекты специфики зрительного восприятия человека, а также эффекты фотографических изображений.

С самого начала формирования компьютерной (машинной) графики как самостоятельного научного направления Институт прикладной математики (ИПМ) им. М.В.Келдыша РАН являлся одним из ведущих научных центров в стране в этой области. В лекции дается обзор основных работ по машинной графике и некоторых связанных с ней областей, проведенных в Институте почти за сорокалетний период.

1. Ранний этап

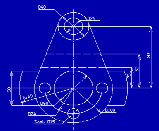
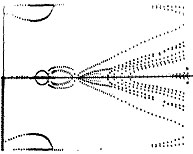
Первые признаки появления нового научного направления относятся к началу 60-х годов прошлого столетия. Знаковым событием считают диссертацию Айвена Сазерленда (1963 г.), в которой были продемонстрированы новые возможности графического интерфейса с машиной в интерактивном режиме [1]. В ИПМ примерно в то же время (1964 г.) был продемонстрирован первый опыт практического применения машинной графики при выводе на характрон последовательности кадров, образующих короткий фильм с визуализацией обтекания цилиндра плазмой (Ю.М.Баяковский, Т.А.Сушкевич) (Рис.1.1).

Новый этап в развитии исследований в области машинной графики связан с появлением в ИПМ (1967 г.) графопостроителя CalComp и векторного дисплея. В 1970 г. был выпущен первый обзор по машинной графике, представленный затем как доклад на Вторую Всесоюзную конференцию по программированию (ВКП-2) [2]. По-видимому, это первая публикация на русском языке, в которой появилось словосочетание (термин) машинная графика .

К 1971 г. в ИПМ для машины SDS -910 был разработан набор подпрограмм, позволяющих снимать кинофильмы [3], установлена камера для покадровой фиксации изображений, выводимых на экран дисплея. С помощью этой системы осуществлялась

Рис. 1.1. Визуализация на характроне процесса обтекания цилиндра плазмой

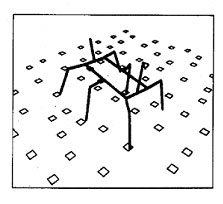
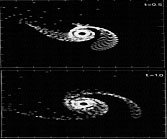
визуализация поведения шагающего робота (рис. 1.2) [4], а также моделирование гравитационного взаимодействия галактик (рис. 1.3) [5]

Рис. 1.2. Моделирование походки робота	Рис. 1.3. Визуализация процесса приливного взаимодействия галактик

1.1. Эпоха Графора

Тогда же, в конце 60-х, началась разработка библиотеки графических программ на Фортране. Первая публикация относится к 1972 г. Тогда библиотека позволяла выводить на графопостроитель, а затем и на дисплей, графические примитивы (отрезок прямой, дуга окружности, алфавитно-цифровые символы) и на их базе строить графики функций. В дальнейшем библиотека пополнилась программами аффинных преобразований, штриховки, экранирования, аппроксимации и сплайн-интерполяции, программами визуализации двумерных функций (поверхности и карты изолиний), программами геометрических построений (рис. 1.4). Графор был реализован на большинстве существующих в то время в Советском Союзе ЭВМ и операционных систем с выводом практически на все имеющиеся графопостроители и графические дисплеи. Этап создания классической графической библиотеки на Фортране завершился в 1985 г. изданием книги [6], которая подводила итог 15-летней работы.

После этого развитие Графора продолжалось еще несколько лет. На персональных компьютерах были реализованы средства ввода с клавиатуры и мышки, соответствующие международному стандарту GKS , был обеспечен вывод информации в форматах TIFF , PCX и метафайла CGM . Завершилось развитие Графора

Рис. 1.4. Примеры изображений, построенных с помощью Графора.

разработкой программ визуализации скалярных и векторных полей на растровых цветных устройствах (1990 г.). Однако спустя десятилетие застоя в научно-технических областях, вызванного развалом СССР и сменой социально-экономической формации, интерес к Графору появился вновь. Ренессанс библиотеки в наши дни связан с ее переносом в среду Windows и Unix [7].

1.2. ГрафиКон: начало международного сотрудничества

На границе 80-х и 90-х годов произошли драматические изменения. Спрос на исследования и разработки на внутрироссийском рынке упал практически до нуля, и вместе с тем исчезли традиционные возможности финансирования. Зато открылись возможности международного сотрудничества. Но это привело к кардинальному изменению тематики и условий работы, а также требований к научно-исследовательским и опытно-конструкторским работам (НИОКР).

В 1990-м году совместно с американской ассоциацией ACM SIGGRAPH при активном участии ИПМ (С.П.Курдюмов, Ю.Ф.Голубев, Ю.М.Баяковский, В.А.Галактионов) началась подготовка международной конференции по компьютерной графике ГрафиКон . Конференция прошла в феврале 1991 года с большим успехом. В ней принял участие целый ряд крупнейших ученых и специалистов в этой области из США и других стран. Среди них Д.Гринберг, А.Ван Дам, Э.Кэтмул, М.Бейли и другие. Конференция стала ежегодной [8] и позволила многим российским специалистам установить контакты со специалистами США, Англии, Франции, Германии, Японии, Кореи, Китая и многих других стран.

Благодаря контактам, установленным на Графиконе в 1992 году, началось международное научное сотрудничество отдела машинной графики Института с японской фирмой ИНТЕГРА [9] в области компьютерной графики и оптического моделирования, которое продолжается уже более десяти лет. Кооперация позволила оснастить отдел компьютерной графики современной техникой и программным обеспечением, сохранить и приумножить квалифицированный кадровый состав, что привело к получению результатов конкурентоспособных на мировом научном рынке.

2. Задача глобальной освещенности: построение фотореалистичных изображений

Магистральным направлением развития компьютерной графики в Институте стало физически аккуратное моделирование распространения света в различных средах. Эта задача сводится к решению задачи глобальной освещенности , когда учитывается не только прямая освещенность поверхностей сцены лучами, идущими непосредственно от источников света, но и вторичная освещенность, создаваемая лучами, отраженными или преломленными другими поверхностями. Все физически обоснованные методы расчета глобальной освещенности являются приближенными решениями интегрального уравнения рендеринга [10]. Трудность решения этого уравнения определяется его рекурсивным характером и сложностью области интегрирования, поэтому на практике применяются приближенные методы численного решения.

2.1. Прямая и обратная трассировка лучей

Для численного решения уравнения рендеринга была построена технология на основе методов Монте-Карло и трассировки лучей , позволяющая с высокой точностью рассчитывать освещенность реальных сцен и строить высокореалистичные изображения фотографического качества [11-12]. Идея метода Монте-Карло прямой трассировки лучей состоит в статистическом воспроизведении механизма распространения света путем моделировании всевозможных траекторий лучей. Траектории световых частиц (фотонов) прослеживаются на всех этапах существования, от момента их генерации источниками света до поглощения или выхода из сцены. Направление, в котором испускается фотон и стартовая позиция на источнике света определяются стохастически согласно фотометрическому распределению энергии источника и его геометрической форме. Траектория фотона трассируется до пересечения с поверхностью.

При взаимодействии фотона с поверхностью, он может быть поглощен, диффузно отражен (преломлен) с равномерной плотностью распределения по полусфере, отражен (преломлен) в зеркальном направлении, или отражен (преломлен) согласно заданной плотности распределения. При выборе дальнейшего поведения фотона согласно свойствам поверхности (например, диффузного или зеркального отражения) используется принцип рулетки.

Метод не зависит от положения глаза наблюдателя и не осуществляет непосредственного вывода изображения на экран, а лишь предоставляет данные об освещенности для алгоритмов закраски изображений, т.е. строит так называемую карту освещенности, которая является решением задачи глобальной освещенности. Метод естественным образом поддерживает все типы поверхностей, включая произвольные сочетания диффузных и зеркальных свойств как при отражении света от поверхностей, так и при его пропускании через прозрачные и полупрозрачные материалы. Для задания нетривиальных оптических свойств поверхности может использоваться двунаправленная функция, описывающая плотность распределения отражений и преломлений (BRDF/BTDF) (см. разд. 5.1).

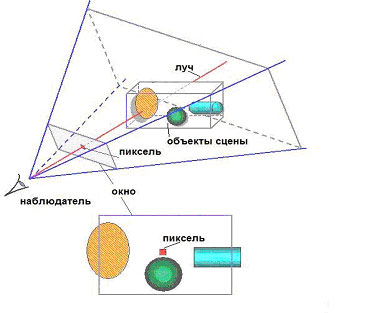
После того как глобальная освещенность сцены рассчитана методом Монте-Карло, ее фотореалистичное изображение можно построить с помощью детерминистического алгоритма обратной трассировки лучей . Алгоритм состоит в испускании в сцену через пиксели экрана одного или нескольких (первичных) лучей (рис. 2.1). Если найдено пересечение луча с объектом сцены, то из точки пересечения в направлении каждого источника света испускаются лучи, отслеживающие затенение. Для незатененной области рассчитывается суммарный коэффициент поглощения света при взаимодействии с встречаемыми на его пути до источника поверхностями и средами. Полученное трассировкой первичных лучей изображение дополняется “зеркальными” отражениями, а также видом через прозрачные поверхности. Для этого алгоритм трассировки применяется к каждому отраженному или преломленному лучу.

Рис. 2.1. Обратная трассировка лучей через глаз наблюдателя и пиксель на изображении.

Созданный на основе этой технологии программный комплекс нашел применение в сфере архитектурного проектирования, дизайна интерьеров, проектирования систем освещения зданий и других объектов городского строительства. Графическая система позволяет при разработке архитектурных и светотехнических решений увидеть, как будет выглядеть интерьер, здание или комплекс архитектурных (инженерных, скульптурных) сооружений в существующем ландшафте при различных условиях естественного или искусственного освещения до начала их реального воплощения. Она позволяет промоделировать, например, несколько вариантов искусственного освещения и/или подбора отделочных материалов для интерьера или здания и выбрать оптимальный. На рис. 2.2 приведены примеры изображений интерьера и внешнего вида здания, являющиеся результатами компьютерного моделирования.

Рис. 2.2. Примеры фотореалистичных изображений, построенных с использованием алгоритмов моделирования глобальной освещенности.

2.2. Модель освещения: искусственный и естественный свет

В графической системе используется физически корректная модель освещения . Параметры освещенности и интенсивности источников света задаются в физических (фотометрических) единицах. Поддерживаются разнообразные типы источников света, включая протяженные источники, условия естественного освещения, а также источником света может быть объявлен любой объект сцены («самосветящиеся» объекты) Для точечных и протяженных источников могут быть назначены гониометрические диаграммы, описывающие угловое распределение излучаемой световой энергии. Система содержит библиотеку предопределенных диаграмм различного характера (рис. 2.3) и позволяет импортировать диаграммы из стандартных форматов IESNA [13].

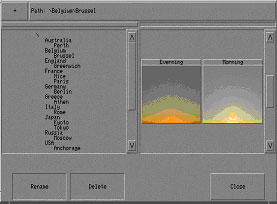
Рис. 2.3. Библиотека источников света и гониометрических диаграмм.	Рис. 2.4. Библиотека параметров солнечного и дневного света. Показаны два режима отображения содержимого библиотеки: слева — в виде списка элементов, справа — в виде окна с графическими иконками.

Для задания естественного освещения можно выбрать подходящий элемент из библиотеки дневного (небесного) и солнечного света (рис. 2.4). Библиотека содержит предопределенные параметры для различных географических регионов (городов) в разное время суток, например, можно выбрать режим освещения, соответствующий естественному дневному свету в Риме, Италия, в 3 часа дня. Можно также с помощью редактора параметров солнечного и дневного освещения задать его в терминах географических координат, даты (времени года) и времени суток, либо в терминах положения солнца (высота над горизонтом и азимут) и освещенности в горизонтальной плоскости. В редакторе также задается степень облачности. Моделирование небесного освещения для случаев 100% облачности и ее отсутствия соответствует стандарту Международной комиссии по освещению CIE [14]. Небесное освещение с неполной облачностью моделируется с использованием интерполяции.

На рис. 2.5 показан пример изображения, на котором воспроизведены условия естественного дневного освещения, а также хорошо видны эффекты отражения/пропускания света стеклянными окнами согласно закону Френеля преломления/отражения света: лучи, падающие на стекло полого, в основном отражаются, а лучи, падающие почти отвесно, в основном проходят сквозь стекло.

Рис. 2.5. Воспроизведение условий естественного дневного освещения и оптических свойств стекла (отражение и преломление света зависят от угла падения).	Рис. 2.6. Фрагмент изображения, на котором воспроизведены явления преломления, зеркального отражения и каустики.

Как подчеркивалось выше, применяемая технология трассировки лучей по методу Монте-Карло позволяет получать высококачественные реалистичные изображения. На рис. 2.6 виден эффект каустики [15] – яркие пятна или полосы, образующиеся в результате многократного преломления и отражения света от криволинейных поверхностей прозрачных объектов.

Каустики являются тонким оптическим эффектом, реалистичная передача которого подтверждает высокий уровень интеллектуальности алгоритмов и программных решений, заложенных в графической системе. Стоит отметить, что каустики нельзя смоделировать с помощью подхода, построенного на методе излучательности ( radiosity ) [11].

2.3. Освещение, основанное на изображении: HDR изображения

Другим, современным, методом задания естественного освещения могут служить изображения с широким динамическим диапазоном яркостей ( High Dynamic Range Images — HDR изображения) реальных сцен [16, 17]. HDR изображение представляет собой сферический, бесконечно удаленный, источник света, который с высокой точностью описывает освещенность реальной сцены. Такие изображения могут быть получены путем специальной обработки нескольких цифровых фотографий с различной экспозицией или результатов панорамного видеосканирования. HDR изображения позволяют использовать ранее зафиксированное освещение реальной сцены (в виде изображения с широким динамическим диапазоном яркостей) в качестве источника света для моделируемой сцены. В результате появляется возможность интегрировать моделируемые объекты с реальным окружением. На рис. 2.7 показана модель автомобиля, «встроенная» в реальный природный ландшафт. Хорошо заметны отражения окружающих деревьев на лобовом стекле, капоте и фарах автомобиля.

Рис. 2.7. Иллюстрация использования изображения с широким динамическим диапазоном яркостей в качестве источника освещения для модели автомобиля.	Рис. 2.8. Пример изображения с широким динамическим диапазоном, полученного с использованием разработанного оператора сжатия.

При этом, однако, возникают проблемы, связанные с отображением изображений с широким динамическим диапазоном яркостей в диапазон яркостей, который может быть воспроизведен на стандартных мониторах и принтерах. Динамический диапазон таких устройств существенно уже (иногда на несколько порядков), чем диапазон яркостей реального мира. Для отображения изображений с широким динамическим диапазоном на стандартных устройствах этот диапазон должен быть сжат до уровня, который может быть воспроизведен на реальных мониторах и принтерах. С этой целью был разработан специальный оператор сжатия (Tone Mapping Operator) [17], который позволяет эффективным образом выполнять такое отображение без потери детальности изображения, с сохранением локального контраста и в отсутствие артефактов. На рис. 2.8 приведен пример изображения с динамическим диапазоном, превышающим 500 000:1, которое было получено с использованием этого оператора.

2.4. Учет специфики фотографических изображений и зрительного восприятия человека

Одним из важных способов повышения реалистичности изображений является учет специфики фотографических изображений и зрительного восприятия человека . Графическая система позволяет воспроизводить некоторые его особенности, в частности, эффект ореолов вокруг ярких источников света — фонарей, ярких бликов на глянцевых поверхностях и пр. (рис. 2.9). Поддерживается также ряд других эффектов фотографических изображений , таких как корона вокруг ярких источников света, дефокусировка изображений, эффект экспозиции при изображении водных поверхностей.

Ореол вокруг ярких источников света . Пример изображения, на котором воспроизведен этот эффект, показан на рис. 2.10. Можно видеть, что ореол формируется не только вокруг первичного источника (фонаря), но и вокруг вторичных источников — бликов на глянцевой поверхности воды. Это относится и к ореолам, видимым человеческим глазом.

Рис. 2.9. Воспроизведение ореолов вокруг ярких источников света в соответствии с особенностями зрительного восприятия человека.	Рис. 2.10. Воспроизведение ореола вокруг яркого источника света и бликов на глянцевой поверхности воды

Ореол, воспроизводимый на фотоизображении, состоит из двух компонентов: лучистой «короны» и блуминга — размытого светового пятна. В ореоле, видимом человеческим глазом, эти два эффекта неразрывно связаны, в то время как в фотоизображении они четко разделены. Это объясняется природой их формирования в процессе фотографирования. Корона образуется, когда свет достигает линзы объектива; блуминг есть результат взаимодействия света с фотопленкой. Поэтому характер двух составляющих зависит от свойств линзы и пленки. В соответствии с этим, в графической системе предусмотрено раздельное управление эффектами короны и блуминга.

Помимо амплитуды ореола и порогового значения светимости, при котором он воспроизводится, можно задавать также число лучей короны, их длину (относительно диаметра изображения) и толщину. Для блуминга задается характер функции затухания и радиус.

Дефокусировка изображения . Если камера сфокусирована на некотором объекте, то на фотографии он будет выглядеть четко, а предметы, расположенные ближе или дальше, будут выглядеть несколько размытыми. Этот эффект поддерживается в процессе визуализации при задании соответствующих опций и параметров фокусирования камеры. Эффект реализован не только для геометрических объектов, но и для источников света.

Эффект экспозиции . Эффект экспозиции воспроизводится для движущихся волнообразных водных поверхностей. Для этой цели используются специальные экспозиционные текстуры. Экспозиционная текстура воспроизводит меняющийся во времени рельеф водной поверхности по заданным параметрам, таким как размеры водного резервуара, его глубина, скорость и направление ветра, диапазон длин волн и число гармоник, максимальное время экспозиции, которое будет использоваться, число «кадров» текстуры, которые будут сгенерированы и их разрешение.

По этим параметрам генерируется серия волнообразных поверхностей, соответствующих моментам времени 0, …, t max , где t max — максимальное время экспозиции. При визуализации сцены с экспозиционной текстурой и заданным ненулевым временем экспозиции t exp ? t max производится суперпозиция волнообразных поверхностей, соответствующих моментам времени из промежутка [0, ..., t exp ]. За счет этого достигается эффект размытости водной поверхности, как на фотографических снимках.

На р ис. 2.11 показаны примеры изображений сцены, содержащей водную поверхность, полученные с нулевым и ненулевым значениями параметра экспозиции. В первом случае вода выглядит как бы застывшей, что редко бывает на реальных фотоизображениях, так как время экспозиции съемки всегда ненулевое. Во втором случае изображение волн в «лунной дорожке» выглядит более правдоподобным.

Рис. 2.11. Изображения водной поверхности в ночное время. Слева — изображение, полученное с нулевой экспозицией, справа — изображение, полученное с экспозицией 1 сек. Хорошо виден также ореол вокруг яркого источника света.

3. Визуализация результатов моделирования

Были разработаны средства визуализации трехмерных распределений физических характеристик (скалярных и векторных полей температур, влажности, воздушных потоков и др.) в их физическом окружении, например, в интерьере здания, в районе застройки домов, в пассажирском салоне автомобиля или самолета или внутри технических устройств, таких как компьютер. В результате повышается информативность изображений, позволяя в наглядной форме представлять связь между характером физического процесса и обуславливающими его внешними факторами. Это может оказаться важным в градостроительстве, при проектировании систем кондиционирования воздуха и отопления, систем охлаждения в приборостроении и компьютерной индустрии и др. Разработанные средства позволяют «накладывать» цветовые карты (тоновая заливка), карты изолиний, векторные поля на реалистичные изображения рассматриваемых сцен в условиях искусственного или естественного освещения [18]. Поддерживается визуализация пространственных скалярных полей, а также трех и четырехмерных векторных полей, заданных на равномерной или неравномерной сетке. Для скалярных полей возможны представления тоновой заливкой и изолиниями на одной или нескольких параллельных плоскостях, а также на трех ортогональных плоскостях. Изолинии могут применяться в сочетании с тоновой заливкой. Скалярные поля можно также изображать в виде изоповерхностей. Трехмерные векторные поля отображаются однотонными векторами переменной длины или разноцветными векторами постоянной длины, где цвет представляет длины векторов. Четырехмерные поля (например, скорость движения воздуха плюс температура) отображаются векторами переменной длины; направление и длина векторов соответствуют трем компонентам, а для представления четвертой служит цвет. Векторные поля визуализируются на заданных пользователем плоскостях в пространстве сцены.

На рис. 3.1 показано изображение здания и обтекающие его воздушные потоки. Стрелки показывают направления перемещения воздушных масс. Абсолютные значения скорости ветра обозначены цветом стрелок. Рис.3.2 иллюстрирует распределение температуры в салоне автомобиля в солнечную погоду с работающим кондиционером, представленное на вертикальной секущей плоскости с полупрозрачной заливкой цветом.

Рис.3.1. Векторное поле воздушного потока вокруг фасада здания	Рис.3.2. Цветовая карта распределения температуры внутри автомобиля.

4. Моделирование сложных оптических систем

Созданная технология расчета распространения света оказалась столь эффективной и точной, что позволила сделать следующий шаг и перейти к моделированию и инженерному проектированию сложных оптических светопроводящих и осветительных систем, таких как жидкокристаллические панели, элементы волоконной оптики, автомобильные фары и приборы и др. Системы такого рода характеризуются многократным количеством внутренних переотражений света.

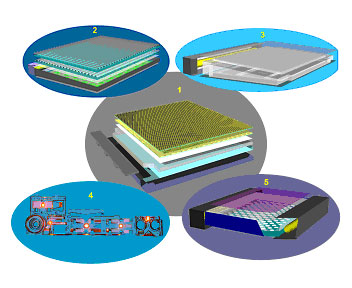
На рис. 4.1 схематично показаны некоторые из таких систем. Приборы, отмеченные цифрами 1, 2, 3, 5, представляют собой осветительные части жидкокристаллических дисплеев (так называемых “ LCD ” мониторов), которые сейчас широко используются, например, в портативных компьютерах. Прибор, отмеченный цифрой 4, представляет осветительный элемент приборной доски современного автомобиля. Как правило, компоненты таких приборов имеют достаточно сложные оптические свойства и геометрию, включая поверхности с микроструктурами. Принцип работы таких устройств основан на эффекте полного внутреннего отражения. Для их моделирования практически невозможно использовать обычные детерминистические методы лучевого расчета распространения света, применяемые для расчета линзовых оптических систем. Наиболее эффективным и физически точным подходом в этом случае является трассировка лучей, основанная на методе Монте-Карло.

Рис. 4.1. Примеры осветительных систем.

4.1. Системы подсветки жидкокристаллических мониторов

Рассмотрим процесс проектирования одного из таких устройств, а именно осветительной части жидкокристаллического монитора (рис. 4.2), более подробно. Конечной целью моделирования подобных систем является расчет пространственного и углового распределений яркости света над выходной гранью устройства (помеченной рамкой на рисунке). Задача заключается в том, чтобы сделать яркость на выходе максимально равномерной.

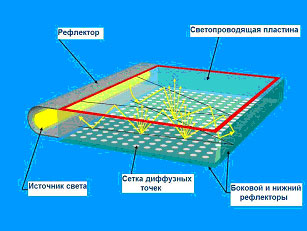
Схематично принцип действия современной системы для подсветки LCD монитора состоит в следующем: свет, излучаемый люминисцентной лампой, попадает через входную грань в акриловую светопроводящую пластину (рис. 4.2) — основной оптический элемент прибора, по которой распространяется путем многократных полных внутренних отражений. На нижнюю сторону этой пластины нанесена сетка диффузных точек, которая рассеивает падающий свет. Свет может выйти из пластины через верхнюю выходную грань в результате диффузного рассеяния от этих точек (рис. 4.2). Все остальные световые лучи падают на верхнюю поверхность под углами, превышающими угол полного внутреннего отражения, что не дает возможности свету выйти за пределы пластины. Поэтому интенсивность выходящего светового потока в точке определяется плотностью распределения диффузной сетки под этой точкой (и в некоторой ее окрестности).

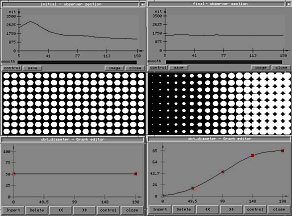
Рис. 4.2. Схема системы подсветки жидкокристаллического монитора .	Рис. 4.3. Иллюстрация процесса проектирования диффузной сетки.

С другой стороны интенсивность света, распространяющегося внутри пластины, падает с расстоянием от входной грани (левая грань на рис. 4.2). Для компенсации этого эффекта плотность диффузной сетки должна постепенно возрастать слева направо, если мы хотим в результате получить на выходной грани равномерное распределение (рис. 4.3). Таким образом, размер диффузных точек, изменяющийся вдоль пластины, или точнее, зависящая от него плотность распределения диффузного материала, является важнейшим параметром при проектировании системы подсветки. В верхней части рис. 4.3 слева и справа показаны графики распределения интенсивности светового потока на выходе системы до начала процесса проектирования и после. Легко видеть, что в результате увеличения размера диффузных точек в направлении слева-направо (рис. 4.3, середина) удается достичь равномерности светового потока на верхней выходной грани. Нижние, редактируемые, графики на рис. 4.3 являются одним из инструментов, позволяющих изменять размеры диффузных точек.