Научный руководитель член-корр. РАН С.П.Курдюмов	Ответственный исполнитель профессор Г.Г.Малинецкий
г. Москва 2002

Аннотация

В проекте предложена целостная, интегративная концепция содержания непрерывного гуманитарного образования на основе современных междисциплинарных подходов и, в частности, синергетики. А кроме того, проанализированы альтернативные стратегии, формы, методы, технологии такого образования с позиций синергетики.
В отчет по проекту включены также материалы, любезно предоставленные Н.Г.Баранцевым и Д.С.Чернавским. Ряд затронутых в отчете проблем более подробно рассмотрены в книгах :
«Новое в синергетике. Взгляд в третье тысячелетие.» Сборник статей под редакцией Г.Г.Малинецкого, С.П.Курдюмова
Д.С.Чернавский «Синергетика и информация»М.Наука 2002
И на сайте http://spkurdyumov.narod.ru/

Содержание

1. Нелинейная динамика и проблемы прогноза—— 4
   • Предсказуемость и анализ сложных систем —— 4
   • Прогноз и динамика сложных социально-технологических систем —— 16
2. Синергетика и принципы коэволюции сложных систем —— 25
3. Имманентные проблемы синергетики—— 33
   • Пределы —— 33
   • Цвишенизм —— 35
   • Креативность —— 38
4. Синергетика и системный синтез—— 44
   • Синергетика в контексте культуры —— 44
   • Системный синтез —— 49
   • Система координат —— 53
5. Кризисы современной России и система научного мониторинга —— 58
   • Системный контекст —— 59
   • Экономические кризисы —— 64
   • Природные катастрофы на рубеже XXI века —— 65
   • Экологические катастрофы на территории России —— 67
   • Стратегические риски в техногенной сфере России —— 70
   • Катастрофы и кризисные явления в современном обществе —— 73
   • Динамика национального достояния как индикатор достоверности оценки социально-экономического развития —— 74
   • К научному мониторингу негативных социально?демографических процессов —— 77
   • Новый подход к прогнозу кризисов в социально?экономических системах —— 78
   • Сценарный подход к управлению риском и ликвидацией последствий
     чрезвычайных ситуаций —— 81
   • Заключение —— 82
6. Методологические аспекты синергетики—— 84
   • Введение —— 84
   • Методология интеграции наук, «всеединство», «универсальный эволюционизм» и
     «физический редукционизм» —— 85
   • Синергетика и логика —— 88
   • Порядок и хаос, логика и диалектика —— 97
   • Порядок и хаос в обществе (проблемы этики) —— 100
7. Заключение —— 106

Проблемы прогноза заслуживают внимания специалистов, в различных областях исследований, по двум причинам. Первая заключается в том, что этими проблемами многие и очень успешно занимаются в России — и в Академии наук, и в высшей школе. И, на наш взгляд, тот громадный потенциал, который сейчас имеется в нашей стране, используется далеко не полностью. Вторая причина связана с тем, что то понимание, которое здесь возникло, относится не только к области прикладной математики. Оно носит достаточно общий характер и существенно меняет взгляд на многие явления и области исследования.
Дальнейшее изложение удобно разбить на две части. В первой речь пойдет о том, что нового внесла нелинейная динамика в анализ такого информационного процесса как прогноз. В частности, обсуждаются установленные в последние десятилетия фундаментальные ограничения на предсказуемость сложных систем, концепция управления риском, гипотеза о «человеческих алгоритмах» прогноза. Во второй части приведено несколько примеров, работающихпоказывающих, как эти идеи применяются при прогнозе поведения сложных социальных систем, а также обращается внимание на новые возможности, открывающиеся в этой сфере.
Предсказуемость и анализ сложных систем
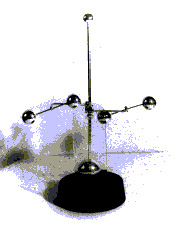
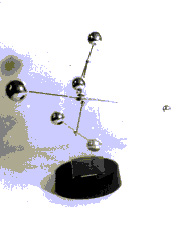
Основные идеи, связанные с прогнозом, можно проиллюстрировать на примере показанного на рис. 1 маятника. Наблюдения авторов за ним показывают, что с вероятностью 95 процентов он будет колебаться непериодическим образом. С вероятностью 5 процентов мы увидим периодическое движение. Это зависит от того импульса, который мы придадим ему вначале. Запустим его и посмотрим, что получится.

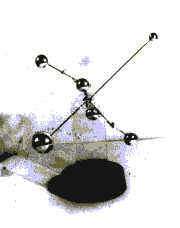Рис. 1. Простейший непериодический маятник, демонстрирующий динамический хаос Чтобы скомпенсировать трение, маятник снабжен магнитиками, а в основание игрушки помещены катушка и батарейка, создающие электромагнитное поле.

До 60?ых годов предполагалось, что есть два класса процессов. Первые — процессы, которые описываются динамическими системами, где будущее однозначно определяется прошлым. Для них, как думали раньше, у нас есть полная предсказуемость. Великий Лаплас, имея в виду такие системы, говорил (если перевести на наш язык), что, располагая достаточно мощными компьютерами, мы сможем заглянуть как угодно далеко в будущее и как угодно далеко в прошлое.
Второй класс процессов — это процессы, где будущее не зависит от прошлого. Мы бросаем игральную кость, и выпадает случайная величина, никак не связанная с тем, что выпадало раньше.
В 70?е годы было понято, что есть третий, очень важный класс процессов, которые формально описываются динамическими системами, как этот маятник. Но, вместе с тем, поведение которых может быть предсказано только на небольшой промежуток времени. А дальше исследователи будут вынуждены иметь дело со статистикой. Для этой игрушки можно написать простую линейную модель, которая позволит нам предсказать, в каком положении, например, окажутся маленькие шарики через пять колебаний большого шарика внизу (естественный промежуток здесь — период колебаний большого шарика.). Используя современные информационные технологии, можно предсказать, в каком положении окажутся они через двадцать колебаний нижнего. Но никакими силами нельзя предсказать их положения через шестьдесят промежутков времени.

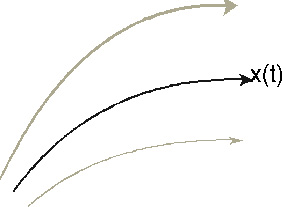Рис. 2. Расходимость фазовых траекторий в системах с динамическим хаосом

Любая динамическая система определяет траекторию в фазовом пространстве, например, такую, как показана черной линией. Динамический хаос обусловлен тем, что соседние траектории, показанные бледными линиями, удаляются от нее. Из-за этого малые причины могут иметь большие следствия.
В 1963 году Рэй Брэдбери опубликовал фантастический рассказ, в котором фактически сформулировал идею динамического хаоса. В этом рассказе один из организаторов предвыборной кампании после победы своего кандидата отправляется в путешествие во времени. Фирма, организующая такую поездку, предлагает охоту на динозавров, которым в ближайшее время суждено умереть. Чтобы не нарушить сложную ткань причинно-следственных связей и не изменить будущее, следует двигаться по специальным тропам. Однако герой не смог выполнить этого условия и нечаянно раздавил золотистую бабочку. Возвратившись назад, он видит, что изменились состав атмосферы, правила правописания и итог предвыборной кампании. Едва заметное движение повалило маленькие костяшки домино, те повалили костяшки побольше, и, наконец, падение гигантских костяшек привело к катастрофе. Отклонения от исходной траектории, вызванные раздавленной бабочкой, стремительно нарастали (см. рис. 2). Малые причины имели большие следствия. Математики называют это свойство чувствительностью к начальным данным.
В том же 1963 году мысль о принципиальной ограниченности нашей способности предсказывать (или, как сейчас говорят, о существовании горизонта прогноза, или пределов предсказуемости) даже в мире, который идеально описывается классической механикой, была высказана лауреатом Нобелевской премии Ричардом Фейнманом. Для существования горизонта прогноза не нужно, чтобы «Бог играл в кости», добавляя в уравнения, описывающие нашу реальность, какие-то случайные члены. Не надо опускаться на уровень микромира, на котором квантовая механика дает вероятностное описание Вселенной. Объекты, поведение которых мы не можем предсказывать на достаточно большие времена, могут быть очень простыми. Например, такими, как представленный маятник.
То, что чувствительность к начальным данным ведет к хаосу, понял — и тоже в 1963 году — американский метеоролог Эдвард Лоренц. Он задался вопросом: почему стремительное совершенствование компьютеров, математических моделей и вычислительных алгоритмов не привело к созданию методики получения достоверных среднесрочных (на 2?3 недели вперед) прогнозов погоды? Эдвард Лоренц предложил простейшую модель, описывающую конвекцию воздуха (она играет важную роль в динамике атмосферы).
Эта модель описывается внешне очень простыми уравнениями[1]

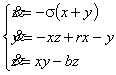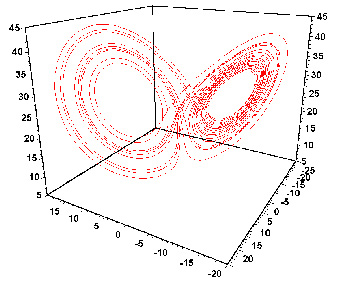Рис. 3. Аттрактор Лоренца

Такая картина, полученная на компьютере (расчет проводился при r=28, s=10, b=8/3), убедила Э. Лоренца, что он открыл новое явление — динамический хаос. Этот клубок траекторий, называемый сейчас аттрактором Лоренца, описывает непериодическое движение с конечным горизонтом прогноза.
где переменная x характеризует поле скоростей, y и z — поле температур жидкости. Здесь r = R/Rc, где R — число Рэлея, а Rc — его критическое значение; s — число Прандтля; b — постоянная, связанная с геометрией задачи.
Компьютерный анализ системы Лоренца привел к принципиальному результату. Этот результат — динамический хаос, т.е. непериодическое движение в детерминированных системах (то есть в таких, где будущее однозначно определяется прошлым), имеющее конечный горизонт прогноза.
Увиденное Лоренцем показано на рис. 3. С точки зрения математики, можно считать, что любая динамическая система, что бы она ни моделировала, описывает движение точки в фазовом пространстве. Важнейшая характеристика этого пространства — его размерность, или, попросту говоря, количество чисел, которые необходимо задать для определения состояния системы. С математической и компьютерной точек зрения не так уж и важно, что это за числа — количество рысей и зайцев на определенной территории, переменные, описывающие солнечную активность или кардиограмму, или процент избирателей, поддерживающих президента. Если считать, что точка, двигаясь в фазовом пространстве, оставляет за собой след, то динамическому хаосу будет соответствовать клубок траекторий. Например такой, как показан на рис. 3. Здесь размерность фазового пространства всего 3 (это пространство x, y, z). Замечательно, что такие удивительные объекты существуют даже в трехмерном пространстве. Для установившихся колебаний, соответствующих динамическому хаосу, Д. Рюэль и Ф. Такенс в 1971 году предложили название — странный аттрактор.
Пророчество Анри Пуанкаре о том, что в будущем можно будет предсказывать новые физические явления, исходя из общей математической структуры описывающих эти явления уравнений, компьютерные эксперименты превратили в реальность.
Система Лоренца имеет конечный горизонт прогноза. Почему? Можно пояснить это следующим образом. Если мы вновь возьмем две близкие траектории, показанные на рис. 3, то они расходятся, как на рис. 2. Одна уходит от второй. Скорость расходимости определяется так называемым ляпуновским показателем, и от этой величины зависит интервал времени, на который может быть дан прогноз. Можно сказать, что для каждой системы есть свой горизонт прогноза [2,3].
Развитие науки показывает, что каждая фундаментальная теория не только давала новые возможности, но и лишала нас иллюзий. Классическая механика лишила иллюзии, что можно построить вечный двигатель первого рода, термодинамика — второго, квантовая механика — что мы можем одновременно сколь угодно точно измерять координату микрочастицы и ее импульс. Теория относительности — что удастся передавать информацию в вакууме со сверхсветовой скоростью. Сегодня нелинейная динамика лишила нас иллюзии глобальной предсказуемости: мы не можем предсказать, начиная с какого-то горизонта прогноза, поведение многих достаточно простых систем и, в частности, этого маятника.
В свое время работа Лоренца была опубликована в метеорологическом журнале, но в течение 10 лет она не была замечена. Метеорологи сегодня полагают, что горизонт прогноза для погоды не превышает трех недель. Т.е. как бы точно мы сейчас ни промеряли параметры атмосферы, предсказать погоду с помощью имеющихся приборов через три недели в данном месте, вообще говоря, невозможно. Горизонт прогноза для состояния океана эксперты оценивают в месяц.
Сейчас многие специалисты по физике Солнца предполагают, что аналогичная ситуация имеет место с Солнцем. Например, известно такое явление, как минимум Маундера, когда в течение почти 70?ти лет всплесков солнечной активности не было. И возникает вопрос, можем ли мы предсказать следующий минимум аналогичного сорта. Те работы, которые проводятся, показывают, что ляпуновские показатели таковы и горизонт прогноза таков, что этого предсказания на несколько десятилетий сделано быть не может.
Однако нелинейная динамика позволила увидеть не только принципиальные трудности, но и новые замечательные возможности. Обратим внимание на одну из них. Давайте посмотрим, сколько нужно чисел для того, чтобы описать эту систему, этот простейший маятник. Классическая наука говорит, что для того, чтобы описать этот маятник, чисел нужно бесконечно много. В самом деле, маятник, очевидно, подчиняется законам механики, но для того, чтобы такая игрушка вращалась и не останавливалась из-за трения, должно создаваться электромагнитное поле. Поэтому — механика плюс электродинамика, уравнения Максвелла. Формально бесконечно много степеней свободы.
Нелинейная динамика, анализируя системы такого сорта, позволяет устанавливать, сколько переменных необходимо для их описания, сколько переменных нужно для прогнозирования, она помогает выяснить, каким должен быть их мониторинг. Оказывается, что для такой системы нужно не более десятка переменных.
Это открывает совершенно новые возможности. У нас есть формально очень сложная система и нам требуется выделить из нее самое главное. Если раньше, в 60-ые гг., был моден системный анализ, рассматривавший некие общие свойства систем, которые возникают у них, как у целого, то сейчас нам в Институте прикладной математики им. М.В. Келдыша РАН очень нравится слово системный синтез. Такой синтез позволяет из массы переменных извлечь именно то, что нужно для принятия решения.
После того, как было понято, что есть принципиальные ограничения в области прогноза, созданы новые поколения моделей и алгоритмов, прогноз стал индустрией. Сейчас происходит скачок в прогнозировании — скачок, который можно сравнить с тем, что произошло с наступлением эпохи персональных компьютеров. До персональных компьютеров ЭВМ были огромными и дорогими комплексами, которые были по силам только очень крупным фирмам. А после появления персональных компьютеров вычислительная техника стала доступна очень многим. Та же самая революция происходит сейчас в области прогнозов. Это перестало быть наукой, это становится технологией. Если раньше «РЭНД корпорейшн» и несколько других коллективов обеспечивали прогнозами правительство США и еще несколько ведомств, то сейчас даже не очень крупные фирмы имеют лаборатории, которые прогнозируют, лаборатории, как их называют, «проектирования будущего».
Динамический хаос позволил в ряде случаев диагностировать серьезные заболевания по данным об электрической активности с помощью довольно простых компьютерных программ, предложить новые алгоритмы сжатия данных и защиты информации. Экономические прогнозы, опирающиеся на представления о хаосе и странных аттракторах, стали бурно развивающейся областью деятельности. Нельзя не вспомнить о «нелинейных журналах» — «Physica D», «Chaos», «Nonlinearity», «Physical Review E», «Прикладная нелинейная динамика» и многие другие. Оказалось, что есть гораздо больше того, что связывает объекты различных научных дисциплин, по крайней мере с точки зрения прогноза, чем того, что их разделяет.

Сейчас в области научных исследований, связанных с прогнозом, в центре внимания находятся описание и предсказание редких катастрофических событий. В свое время один из создателей современной химии Вант-Гофф говорил: «Я убрал из своих трудов все то, что трудно наблюдать, и то, что происходит достаточно редко». Возможности, которые дают нам сегодня информационные технологии, позволяют обратиться к анализу и прогнозу редких катастрофических событий.
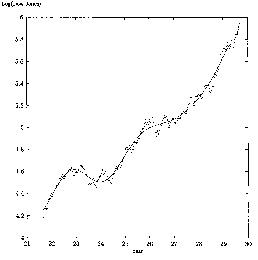
Приведем пример, показывающий, что самые разные катастрофические события могут развиваться по одним законам. На рис. 4 показаны графики поведения характеристик, описывающих две сложно организованные иерархические системы — фондовый рынок и тектонический разлом — незадолго перед катастрофой.
Как видим, в обоих случаях, у нас есть быстрый катастрофический рост, на который накладываются ускоряющиеся колебания. Сглаженная кривая отлично описывается формулой

т.е. мы имеем одно и то же решение уравнений, которых пока не знаем. Следует обратить внимание на то, что асимптотикой таких процессов перед катастрофой является так называемый режим с обострением (когда одна или несколько величин, характеризующих систему, за конечное время вырастают до бесконечности). Этот класс режимов в течение более 30?ти лет исследуется в научной школе, сложившейся в Институте прикладной математики им. М.В. Келдыша РАН, под руководством одного из авторов этого сообщения. Последняя книжка на эту тему «Режимы с обострением. Эволюция идеи» вышла в прошлом году в издательстве «Наука» [6].
В свое время Джон фон Нейман говорил: «Я не верю, что можно найти общие закономерности в поведении сложных систем. Это то же самое, что построить теорию не слонов». Развитие нелинейной динамики опровергло это утверждение. Нелинейная динамика позволила установить универсальные сценарии возникновения хаоса из упорядоченного состояния [3]. То, что происходит сейчас в науке, показывает, что в ряде случаев можно говорить и о неких универсальных сценариях возникновения катастроф.

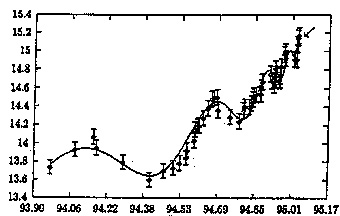Рис. 4. Характерный вид зависимости, возникающей перед катастрофами в сложных системах Слева — зависимость логарифма индекса Доу-Джонса (этот индекс определяется ценой самого эффективного пакета акций 30?ти ведущих компаний Соединенных Штатов) от времени перед Великой депрессией с 1921 по 1930 год. Точки — это точные данные, а сплошная кривая — сглаженная зависимость, простроенная по ним. [4] Справа — зависимость логарифма концентрации ионов хлора в родниках перед катастрофическим землетрясением в Кобе в 1995 году от времени (указано в годах). [5]

Лет тридцать назад Ричарда Фейнмана спросили: «Если бы завтра все живущие ныне физики погибли и от всех них в будущее можно было бы передать только одну фразу, что бы Вы сказали?» «Весь мир состоит из атомов и пустоты, — ответил Фейнман. — Остальное они додумают».
Если бы такой же вопрос сейчас был задан всем ученым, а не только физикам, вероятно, фраза должна была бы быть иной: «Научитесь управлять рисками». Управление рисками — одна из важнейших технологий нашей цивилизации [7,8]. Она соответствует магистральному пути прогресса — менять одни угрозы и опасности на другие. Например, опасность голодать и мерзнуть — на риск пожинать плоды заражения воды, земли, воздуха, связанные с работой тепловых или атомных станций.
Не надо думать, что здесь «иного не дано», что здесь можно только плыть по течению. Иное дано. Швеция приняла решение отказаться от атомной энергетики как от слишком опасной технологии. В то же время во Франции, где более 70 процентов электроэнергии производится на АЭС, правительство рассматривает форсированное развитие этой отрасли как важнейший способ сохранения окружающей среды. Цена вопроса весьма высока, и свобода маневра достаточно велика.
Глубокая связь между идеями нелинейной динамики и управлением рисками стала ясна недавно. Осознать ее помогла парадоксальная статистика аварий. Вспомним «Титаник», «Челленджер», Чернобыль, Тримайл, Бхопал… Каждая из этих крупнейших катастроф XX века связана с длинной цепью причинно-следственных связей, с «неблагоприятным стечением многих маловероятных случайных обстоятельств», как часто пишут в актах государственных комиссий. И в самом деле, вздумай злоумышленник специально сделать что-то подобное, ему пришлось бы трудно. При знакомстве с бедствиями не оставляет чувство, что нам просто очень не везет.
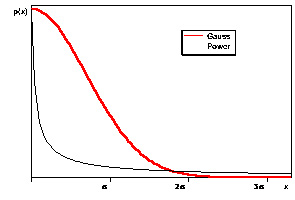
Что же является математическим образом этого «невезения»? Выше уже звучало слово «случайность». В начале прошлого века Карл Гаусс установил, что сумма независимых, одинаково распределенных случайных величин подчиняется вполне определенному закону. Соответствующая ему кривая, получающаяся после нормировки, показана на рис. 5. Видно, что она очень быстро убывает, большие отклонения, в соответствии с этим законом, очень редки. Настолько редки, что ими можно пренебречь.

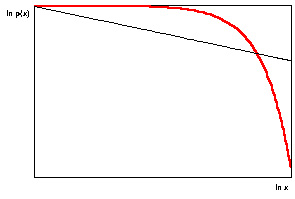Рис. 5. Типичный вид нормального и степенного распределений Классическим, привычным является гауссово распределение (жирная линия). В соответствии с ним, большие отклонения настолько редки, что ими можно пренебречь. Однако многие бедствия, аварии, катастрофы порождают статистику со степенным распределением (тонкая линия). В этом случае редкими катастрофическими событиями пренебречь нельзя. На правом рисунке графики тех же распределений представлены в логарифмическом масштабе, при котором степенные зависимости приобретаю вид прямых линий.

Гауссово распределение лежит в основе множества инженерных расчетов и технических норм. Все инженеры знают, что есть «правило трех сигм». Это правило говорит о том, что вероятность отклонения случайной величины от среднего значения более, чем на три «сигмы» составляет менее 0,001 (см. рис. 5). «Сигма» здесь — среднеквадратичное отклонение.
Простой пример: по этому закону распределен рост людей. Поэтому вероятностью встречи с трехметровым гигантом с легким сердцем можно пренебречь.
Но есть и другой класс законов, которые называют степенными (тонкая кривая на том же рисунке). Здесь «хвост» убывает гораздо медленнее, поэтому такие законы часто называют «распределениями с тяжелыми хвостами». В этом случае большими отклонениями пренебречь нельзя. Если бы по такому закону был распределен рост, то это был бы уже мир восточных сказок с тридцатиметровыми джиннами, ифритами, дэвами, которые вполне могли встретиться в жизни простых смертных.
Именно в мире восточных сказок мы обычно и оказываемся, сталкиваясь с бедствиями, катастрофами, авариями. Такова статистика землетрясений, наводнений, ураганов, инцидентов с хранением ядерного оружия, биржевых крахов, ущерба от утечки конфиденциальной информации, многих других невзгод.
Чтобы не быть голословным, приведем американскую статистику за последний век (рис. 6). По оси абсцисс отложено число жертв, а по ординате число событий, в которых число жертв было больше заданной величины. Здесь представлены торнадо, землетрясения, наводнения, ураганы. Идеальной степенной статистике соответствовала бы прямая. Видим, что экспериментальные данные с достаточно хорошей точностью ложатся на прямые.
Почему это жизненно важно? Когда мы определяем, браться ли нам за какой-то технический проект или не браться, то есть несколько подходов. Первый подход был реализован и доведен до совершенства еще во времена Колумба.
Мы считаем все возможные исходы N, берем их вероятности pi, умножаем на соответствующие выигрыши или проигрыши xi и суммируем

И в зависимости от того, какая величина получится, мы беремся за этот проект или не беремся.

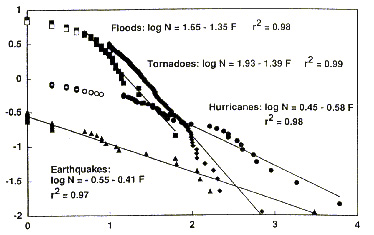Рис. 6. Распределение бедствий по количества погибших в их результате в США в XX веке По оси абсцисс отложена фатальность F стихийного бедствия, измеряемая логарифмом числа погибших в его результате. Логарифм числа бедствий (log N), имеющих фатальность не меньше данной отложен по оси ординат. Идеальным степенным законам соответствуют прямые. Видно, что эти законы являются хорошим приближением для реальной статистики бедствий и катастроф. Приведены данные для торнадо (ромбы), наводнений (квадратики), ураганов (кружки), землетрясений (треугольники).

Следует отметить, что единственной экспедицией, которая пошла за государственный счет в Новый Свет, была экспедиция Колумба. А после этого в Испании торговые дома начали заниматься страхованием и перестрахованием таких проектов, потому что финансовый риск для отдельного торгового дома был слишком велик. Но зато и выигрыш был очень велик.
Исторический анекдот: Френсис Дрейк после своей экспедиции в Новый Свет преподнес английской королеве подарок, который равнялся двум годовым бюджетам Англии. И королева расплатилась со всеми долгами.
Итак в нашем мире действительно есть много очень опасных, но очень выгодных проектов. И на этой основе, заложенной еще во времена Колумба, до 50-х годов оценивались очень многие технические инициативы.
Однако еще в XVIII веке был замечен следующий парадокс. Представим такую игру: мы бросаем монетку — выпадает орел или решка. Если выпал орел, Вы получаете два золотых дуката и игра кончается. Если он выпал во второй раз, Вы получаете четыре золотых дуката и игра кончается. Если третий раз, — восемь. При этом сумма S1, которая входит в «колумбов алгоритм» бесконечна.
Спрашивается, сколько можно заплатить за право войти в такую игру? Бернулли, который был в Санкт-Петербурге и наблюдал за такой игрой, был поражен тем, что люди готовы платить за это не более 20 дукатов.
Когда человек оценивает вероятность и решает, следует ли рисковать, то, по мнению Бернулли, он действует не по «колумбову алгоритму». Он оценивает не реальный выигрыш, а полезность выигрыша

где U(xi) — функция полезности. Если у Вас есть рубль, то 100 рублей для Вас — огромный выигрыш. А если у Вас есть тысяча рублей, то 100 рублей Вы цените гораздо меньше, его «полезность» для Вас гораздо меньше. В середине ХХ века Джон фон Нейман показал, что в экономическом поведении для массы ситуаций «бернуллиевский алгоритм» хорош.
Однако дальнейшие исследования экономического поведения, в частности, работы Алена и его школы, показали, что алгоритм принятия решений у людей во многих ситуациях иной, более сложный. Человек имеет дело не с формулой Бернулли, а с формулой, где есть не только функция полезности, но и субъективные вероятности, отражающие наши представления об опасности

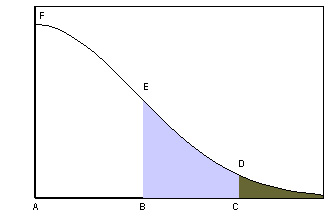Рис. 7. Типичная схема оценки аварий В случае «гауссовых бедствий» выделяют проектные, запроектные и гипотетические аварии. Вероятность первых определяется площадью криволинейной трапеции ABEF, запроектных — BCDE, гипотетических — площадью участка под кривой, лежащим справа от линии DC. Для наглядности площади, соответствующие запроектным и гипотетическим авариям, на рисунке значительно увеличены.

где f(pi) — субъективные вероятности [9]. Они отражают наше мнение о том, насколько вероятно то или иное событие. Психологи утверждают, что если человеку сообщают, что риск меньше 10?6 годУ1, то он просто игнорирует эту возможность.
То есть для того, чтобы анализировать какие-то проекты, мы должны иметь не-кую систему оценок. В 50?е годы предполагалось, что люди, если им регулярно платят зарплату и они имеют достаточную квалификацию, способны обеспечить абсолютную безопасность работы любого объекта. Но благодаря Государственной научно-технической программе «Безопасность», усилиям член-корр. РАН Н.А. Махутова, удалось показать, что здесь разумнее действовать так, как действуют во всем мире, а именно, так, как показано на рис. 7.
Итак: у нас есть проектные аварии (и для них есть некая вероятность). А раз они проектные, то компания должна их устранять сама. У нас есть запроектные аварии со своими вероятностями — их последствия должны ликвидировать МЧС, соответствующие органы, которые могут это делать. И есть еще гипотетические аварии, вероятностью которых, как еще недавно считали, можно пренебрегать.
Исходя из этой картинки, проектировалось очень многое, начиная с систем вооружений и кончая атомными станциями. Оказалось, что предположение о гауссовой статистике, собственно, и приводит к заключению о том, что возможность вероятности аварии на атомной станции 10?7 годУ1, т.е. одна авария за 10 миллионов лет. Однако, как показали проведенные в последние годы исследования, во всех этих случаях мы имеем дело со степенной статистикой. Поэтому оценки должны быть совершенно другие.
Защищаться от «степенных катастроф» нужно совсем иначе, чем от обычных «гауссовых аварий». Среди последних можно выделить проектные (иногда возникающие), запроектные (которые бывают совсем редко) и гипотетические аварии (настолько редкие, что ими обычно пренебрегают). А в случае «степенных бедствий» надо рассчитывать на худшее. В случае землетрясений нужно не надеяться «на авось», а вести сейсмостойкое строительство. Другой пример: плотины Волжского каскада закрывают водохранилища, содержащие десятки кубических километров воды. Их разрушение может привести к возникновению волны в десяток метров высоты. Это сотни тысяч жизней.

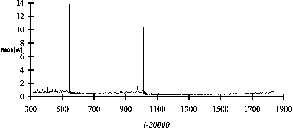Рис. 8. Типичная картина при возникновении жесткой турбулентности На «хаотическом фоне» изредка возникают гигантские пики.

Чтобы представить масштаб редких катастрофических событий, достаточно напомнить несколько эпизодов из истории XX века. При наводнении 1931 года на реке Янцзы в Китае погибло 1,3 млн. человек, при Тянь-Шанском землетрясении в 1976 году — около 650 тысяч. Наводнение в Бангладеш в 1970 году унесло более 500 тысяч жиз-ней и оставило без крова 28 млн. человек [8].
В управлении риском основное и наиболее важное связано не только с описанием, со статистикой, с пониманием механизмов. Главное связано с тем, что в ряде случаев можно определить предвестники. Пример такого поведения дает интересное явление, которое называется жесткой турбулентностью. В 70?х годах его обнаружили в физике плазмы, а в последнее время в самых разных системах типа «реакция-диффузия». Пусть есть некая величина, которая меняется в хаотическом режиме, но иногда совершает гигантские скачки (см. рис. 8). И вот для таких модельных задач удается выявить предвестники, которые сигнализируют об опасности. Еще ничего не произошло, катастрофа далеко, а некоторая медленно меняющаяся переменная уже говорит о том, что мы вошли в опасную область (рис. 9).
Сейчас такие вещи ищутся для многих реальных систем.

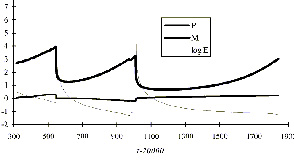Рис. 9. Изменение медленных переменных перед гигантскими пиками Наиболее важна с точки зрения предупреждения катастрофических событий переменная M(t).

Ряд усилий, связанных с разработкой и приложением теории управления риском, предпринимается в связи с принятой по инициативе МЧС России Федеральной целевой программой по предупреждению и смягчению последствий чрезвычайных ситуаций в природной и техногенной сфере. В этой программе акцент сделан на прогнозе и предупреждении бедствий и катастроф, поскольку прогноз и предупреждение, с экономической точки зрения, обходятся в десятки, а иногда и в сотни раз дешевле, чем в ликвидация последствий уже происшедших бед.
Многие глобальные проблемы проявляются прежде всего в росте масштабов и числа чрезвычайных ситуаций. Без перелома этой тенденции не приходится надеяться на выход страны на траекторию устойчивого развития. Для России все это особенно актуально.
Однако масштаб этих работ в стране, на наш взгляд, пока не соответствует их значению. Здесь нужен широкий междисциплинарный подход и гораздо более активное участие Академии наук. Многие вещи здесь должны быть пересмотрены и переоцене-ны.

Откуда берется степенная статистика? Ответ на этот вопрос дает новая парадигма нелинейной динамики — парадигма сложности и построенная в ее рамках теория самоорганизованной критичности [10,11].
Степенные зависимости являются характерной чертой многих сложных систем — разломов земной коры (там это знаменитый закон Рихтера-Гутенберга), фондовых рынков, биосферы на временах, на которых происходит эволюция. Они типичны для движения по автобанам, трафика сообщений через компьютерные сети, многих других систем.
Для всех этих систем общим является возникновение длинных причинно-следственных связей. Одно событие может повлечь другое, третье, лавину изменений, затрагивающих всю систему. Например, мутация с течением времени меняющая облик биологического вида, влияет на его экологическую нишу. Изменение экологической ниши этого вида, естественно, влияет на экологические ниши других видов. Им приходится приспосабливаться. Это опять меняет экологические ниши. При этом окончание «лавины изменений», переход к новому состоянию равновесия могут произойти не скоро.
Простейшей физической моделью, демонстрирующей такое поведение, является куча песка.
Представим следующую картину. Мы бросаем песчинку на самый верх кучи песка. Она в состоянии либо остаться на ней, либо вызвать лавину. В лавине может быть одна или две песчинки, а может быть очень много. Оказалось, что статистика для кучи песка является степенной, так же как для ряда бедствий и катастроф. Она очень похожа на ту статистику, которую мы имеем, скажем, для землетрясений и для многих других сложных систем. То есть опасность находится на грани между детерминированным и вероятностным поведением или, как сейчас говорят, на кромке хаоса.
Исследование сложных систем, демонстрирующих самоорганизованную критичность, важно не только с прикладной точки зрения. Оно меняет отношение к сложным системам. Критическое поведение характерно для фазовых переходов, для самых разных систем вблизи точки потери равновесия. Принципиальным моментом, который удалось осмыслить и математически описать, стал самоорганизованный характер критичности во многих сложных системах. Оказалось, что такие системы сами по себе стремятся к критическому состоянию, в котором возможны лавины любых масштабов.