Жизнь ведь тоже только миг,
Только растворенье
Нас самих во всех других
Как бы им в даренье.

Б. Пастернак

Время проходит, меняются задачи, появляются новые проблемы, и в соответствии с этим становится иным взгляд на прошлое. Кроме того, формируется новый образ будущего, стратегии и цели развития. Поэтому при самом добросовестном отношении к знанию, истине и науке историю вновь и вновь переписывают, чтобы осмыслить вчерашний день с позиции завтрашнего.

Выдающийся специалист по прикладной математике, междисциплинарным исследованиям, философии и методологии науки, член-корреспондент РАН, мой учитель, Сергей Павлович Курдюмов говаривал по этому поводу: «Будущее временит настоящее и проясняет прошлое» (см. рис. 1). Кроме того приходят следующие поколения, которым хочется передать результаты, надежды, мечты предыдущих и, если получится, уберечь от уже сделанных ошибок.

Рис. 1. Сергей Павлович Курдюмов (1928–2004).

Именно с этих позиций сейчас хотелось бы взглянуть на научное творчество С.П. Курдюмова, на идеи, которые выдвигал он сам, и которые сейчас развивает его научная школа.

О личности Сергея Павловича, о его взглядах на жизнь, науку, будущее замечательно рассказывает книга воспоминаний о нем, которую успела подготовить писательница Зоя Журавлёва [1]. Сергей Павлович со школьных лет вел подробные дневники, в которых впечатления и раздумья перемежались с формулами. Зоя Журавлёва настояла, чтобы эти дневники, писавшиеся наскоро, были расшифрованы, и часть их была представлена в этих воспоминаниях.

О многом проще сказать «от первого лица». Сергей Павлович, размышляя, перечитывал записи, сделанные им в разные годы. «Удивительно, но одни и те же мысли приходили и возвращались вновь и вновь, начиная со школьных лет», — несколько раз говорил он мне. Казалось бы, внешние события его большой жизни уже описаны. На 70-летнем рубеже он задумался, какие из его работ и идей, хотелось бы «передать в будущее». Поэтому мы подготовили сборник «главных работ» научной школы с комментариями к ним [2], который потом издавался и переиздавался.

Сергей Павлович умел «любить науку в себе, а не себя в науке» и обычно радовался успехам и достижениям учеников и коллег больше, чем своим. Он считал, что мы делаем общее дело, работаем на будущее, и что самое главное и интересное – впереди. Когда мы получили тираж этого сборника, то он сразу подарил больше трех десятков экземпляров своим коллегам, друзьям и ученикам. При этом он, подписывая, не только адресовал теплые слова, но и там же написал каждому задачу, которую очень важно было бы решить в будущем. Каждому свою. Сергей Павлович был очень щедрым человеком – он с удовольствием дарил своё внимание, мысли, время, идеи и задачи тоже.

В своё время ученики коллеги и друга С.П. Курдюмова – В.Б. Уварова, специалиста по уравнениям состояния, крайне важным при моделировании ядерных взрывов и в задачах астрофизики, после его смерти издали монографию, посвященную развивавшимся им идеям. «Продолжить дело учёного, пойти дальше, превзойти его – это и есть лучший памятник ему. Дело его надо продолжать, а не мраморные глыбы ставить!», — с воодушевлением говорил Сергей Павлович.

Поэтому, наверно, стоит рассказать о нескольких главных идеях Сергея Павловича, об «инвариантах» его научного творчества, к которым он возвращался вновь и вновь на своём жизненном пути.

Хотя этот текст рассчитан «на всех», в нем иногда будут встречаться формулы. Мы как-то обсуждали с Сергеем Павловичем план и стиль одной из наших научно-популярных брошюр и уместность в ней формул. Я приводил ему слова выдающегося физика и блестящего популяризатора Стивена Вайнберга: «Каждая формула в научно-популярной книге уменьшает число читателей книги вдвое» и отстаивал «текст без формул». «Для математиков, физиков, естественников формулы выразят проще, точнее и конкретнее то, что мы хотим. Гуманитариям мы расскажем то же самое, но формулы напомнят им, что есть и другой язык. И это сила, а не слабость», – возражал мне Сергей Павлович.

По его инициативе и самом активном участии Зои Журавлёвой и ассоциации «Женщины в науке и образовании» была организована целая серия замечательных конференций «Языки науки, языки искусства.» Поэтому формулы иногда будут попадаться.

Сергей Павлович был одним из основоположников теории самоорганизации или синергетики (от греческого – совместного действия), – междисциплинарного подхода, который активно развивается в отечественной и мировой науке с 1970-х годов. Его исследования и работы его научной школы получили мировое признание.

Однако, как говорили восточные мудрецы, которых любил вспоминать Сергей Павлович: «Сначала мы выбираем Путь, а потом Путь выбирает нас». Применительно к науке это означает, что мировоззрение, идеи и мечты в большой степени определяются задачами, которыми занимается исследователь.

Прикладная математика, как основа мировоззрения

Природа смеется над трудностями интегрирования

П.С. Лаплас

Вся научная жизнь Сергея Павловича прошла в Институте прикладной математики (ИПМ) АН СССР, а позже в ИПМ им. М.В. Келдыша РАН. Этот институт был создан в 1953 году выдающимся советским математиком, механиком, организатором науки, академиком Мстиславом Всеволодовичем Келдышем для решения стратегических задач, стоявших перед страной, которые требовали математического моделирования и компьютерных расчётов. Институт сыграл огромную роль в реализации советского ядерного и космического проектов. Благодаря этим проектам нынешняя Россия и существует сейчас как суверенное государство.

Срочная важная работа на переднем крае науки требовала квалифицированных, самоотверженных, талантливых людей. С другой стороны, именно работа над такими задачами помогала выращивать выдающихся учёных, позволяла создавать новые области науки, порождала новые идеи и необычный взгляд на мир.

Чтобы понять новое, естественно сравнить его со старым. Основным инструментом в Институте, где работал Сергей Павлович и которым позже руководил, была прикладная математика. Наверно, с неё и стоит начать.

В ХХ веке произошла важная бифуркация в развитии науки. Напомним, что бифуркация (от французского – раздвоение, ветвление) в строгом смысле — это изменение числа и/или устойчивости решений определённого вида при варьировании параметров. В более широком смысле, и в гуманитарных науках, и в массовом сознании, с этим понятием связывается ситуация, в которой предыдущая траектория системы теряет устойчивость и появляются новые возможности для развития, другие траектории.

Математика едина, но в XIX веке сначала неявно, а затем явно произошло разделение на «теоретическую» и «прикладную» математику. Дело в том, что в XVIII веке учёные не обращали особого внимания на строгость доказательств, на теоремы существования и единственности. Член Санкт-Петербургской академии наук Леонард Эйлер полагал, что работа учёного – делать выкладки, а их строгое обоснование – дело второстепенное. Однако, Коши, Вейерштрасс, другие учёные столкнулись с парадоксами, возникающими при переходе к пределу в ряде задач математического анализа, а позже и с логическими задачами, не имеющими убедительных, очевидных решений. Требования к строгости возросли. Стало ясно, что прежде, чем вычислить ответ, надо доказать, что решение задачи существует и единственно. Это потребовало больших усилий и работы многих талантливых людей.

С другой стороны, потребности техники, физики, механики, астрономии ставили множество сложных проблем. При этом приходилось применять различные приближенные методы, уточнять постановку задач, самым активным образом взаимодействовать со специалистами, которым нужно решение.

Например – авиационная и космическая техника, судостроение и множество задач, связанных с обороной, требуют описания движения вязкой жидкости или газа. Классической моделью, описывающей такое движение, является выведенное столетия назад уравнение Навье–Стокса. Однако у нас до сих пор нет доказательств существования и единственности решений этого замечательного уравнения в трехмерной постановке. Однако именно в такой постановке можно описывать сложные, хаотические – турбулентные — движения жидкости и множество других важных и интересных явлений. И это уравнение нельзя «отложить на потом». Надо строить более простые модели, учиться считать их на компьютере, сопоставлять вместе со специалистами-гидродинамиками с экспериментом, уточнять модели и т.д. Именно этим и занимается прикладная математика.

Иногда шутят: «Теоретическая математика делает то, что можно, так, как нужно, а прикладная – то, что нужно, так, как можно».

Отсюда появляется и два взгляда на математические науки, отличающиеся расстановкой акцентов. Первый взгляд очень точно определил математик и популяризатор науки В.А. Успенский [3]: «Автору очень хочется сказать, что математика – единственная наука, где достигается абсолютная истина, но он всё же на это не решается, так как подозревает, что абсолютность истины не достигается нигде. Но в любом случае математические истины ближе к абсолютным, чем истины других наук. Поэтому математика – наилучший полигон для тренировки на истину. Истина – основной предмет математики».

Такая трактовка широко распространена на механико-математическом факультете МГУ. Студенты других факультетов часто в шутку называют мехматян «носителями высшего знания».

Да и, собственно, о какой истине мы говорим? Только в классической философии есть две принципиально различные концепции истины. Одна из них основывается на принципе корреспонденции как соответствия знания объективному положению дел предметного мира (Аристотель, Ф. Бэкон, Дидро, Фейербах, Ленин). Другая – на принципе когеренции как соответствия знания характеристикам содержания идеальной сферы: Абсолюта (Платон, Гегель и др), врождённым когнитивным структурам (Августин, Декарт), априорным формам (Кант), интерсубъективным конвенциям, соглашениям (А. Пуанкаре) и т.д. В постмодерне рассматриваются «игры истины в отношении индивидуума к самому себе» (Фуко). Тот же философ рассматривал «историю истины» как создание «такой истории, которая была бы не историей того, что может быть истинного в знаниях, а анализом «игр истины», игр истинного и ложного, игр, через которые бытие исторически конструирует себя как опыт, то есть как то, что может и должно быть помыслено» [4]. Как видим, и с «истиной» не всё просто. Другим любимым утверждениям «теоретических математиков» является положение, что «математика – это язык» и «сфера творчества».

И действительно, после открытия Н.И. Лобачевским первой неевклидовой геометрии, а впоследствии и множества других, после создания в ХХ веке нескольких вариантов математического анализа (например, в нестандартном анализе вводится отдельное пространство «бесконечно малых чисел», отличных от всех других) стало ясно, что разных «математик» может быть много. И здесь уместна трактовка математики как «науки о возможных мирах», данная Вильгельмом Лейбницем.

Однако эта произвольность открывает возможность для творчества. Поэтому, к примеру, во многих американских университетах математические факультеты находятся в отделениях изящных искусств. Но есть и совершенно другой взгляд на математику, делающий акцент на прикладном аспекте этой дисциплины.

В этом контексте первична именно «прикладная», а не «теоретическая» математика. Именно так смотрел на науку, которой занимался, Сергей Павлович.

Этот взгляд очень точно выразил выдающийся российский исследователь, академик Владимир Игоревич Арнольд – представитель теоретической математики: «Вся математика делится на три части: криптография (оплачиваемая ЦРУ, КГБ и им подобными), гидродинамика (поддерживаемая производителями атомных подводных лодок) и небесная механика (финансируемая военными и другими организациями типа НАСА, имеющими отношение к ракетам).

Криптография привела к созданию теории чисел, алгебраической геометрии над конечными полями, алгебре[1], комбинаторики и компьютеров.

Гидродинамика породила комплексный анализ, уравнения в частных производных, теорию групп и алгебр Ли, теорию когомологий и методы вычислений.

Небесная механика дала начало теории динамических систем, линейной алгебры, топологии, вариационному исчислению и симплектической геометрии.

Существование таинственных связей между всеми этими различными областями – самая поразительная и прекрасная сторона математики (не имеющая никакого разумного объяснения)» [5].

С.П. Курдюмов и В.И. Арнольд были знакомы, относились с симпатией друг к другу и даже говорили о совместных исследованиях, но не успели. В своё время в Московском физико-техническом институте (МФТИ), в котором Сергей Павлович много лет преподавал, а затем заведовал кафедрой прикладной математики, была позиция заведующего кафедрой математики. На неё претендовал В.И. Арнольд – исследователь с мировым именем. К сожалению, ученый совет отклонил эту кандидатуру, о чём Сергей Павлович не раз с сожалением вспоминал. В.И. Арнольд не раз говорил, что математика – часть физики.

Этих исследователей многое связывало и по существу, в научном пространстве, Оба считали, что главным действующим лицом математики, естествознания, да и науки в целом будет нелинейность. Сергей Павлович часто говорил на своих лекциях: «Мы вступили с вами в новый мир – мир нелинейных процессов».

Для линейных уравнений справедлив принцип суперпозиции (наложения), встречающийся нам постоянно, начиная со школьной программы, где он упоминается в связи с законом Кулона. Благодаря принципу суперпозиции через наш радиоприёмник одновременно приходят сигналы тысяч радиостанций, не мешая друг другу, и мы можем их «поймать», покрутив ручку настройки.

Если L – линейный оператор, то в соответствии с принципом суперпозиции

L(αu + βν) = αLu + βLν.                                                                                               (1)

Или «на гуманитарном языке» – в линейном мире действие совокупности причины 1 и 2 является обычной арифметической суммой результатов причины 1 (как будто второй не существует) и 2 (как будто не существует первой). Именно принцип суперпозиции позволяет «разделять и властвовать», «собирая» общее решение линейной задачи из частных. Иногда математическую физику, которую проходят в университетах, называют «наукой о трех уравнениях», – теплопроводности, Лапласа и колебаний струны –

u_t = u_xx , Δφ=0, ν_tt - ν_xx = 0 .                                                                                       (2)

С нелинейными уравнениями, которыми занимался Сергей Павлович, всё гораздо сложнее и интересней. Он часто говорил примерно так: «Мир един, поэтому его главные свойства можно выяснить на самых простых моделях», – и приводил такой пример. Уравнение Мальтуса описывает рост популяции N со временем t

                                                            (3)

Его решение – экспонента – она неограниченно растет за бесконечное время (α – постоянная, называемая мальтузианским коэффициентом). Мальтус полагал, что в соответствии с этим законом (в равное число раз за равные промежутки времени) растет численность человечества. И в этом он ошибался.

Однако уже простейшее нелинейное уравнение

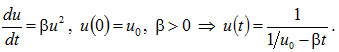
ведёт себя гораздо интереснее. Здесь u(t) стремиться к бесконечности за конечное время, называемое временем обострения t_f. И это время существования зависит от начальных данных. Исследования, проведённые профессором Сергеем Петровичем Капицей, показали, что именно по этому, гиперболическому закону численность человечества росла около миллиона лет. Именно это кардинально отличает нас от всех видов, живущих на Земле. Если бы складывавшаяся в течение сотен тысяч лет тенденция сохранялась бы, то «временем обострения», когда нас стало бы бесконечно много, стал 2025 год (на Западе иногда это время называют точкой сингулярности). Удивительно простое уравнение оказывается содержательным и отражающим ключевые вещи, касающиеся каждого из нас. Сергей Павлович был дружен с профессором Физтеха, выдающимся просветителем и бессменным ведущим передачи «Очевидное–невероятное». По словам С.П. Капицы именно в ИПМ, на семинаре у Сергея Павловича его глобальная демографическая теория нашла понимание и поддержку. Оба они очень ценили свою совместную монографию [6].

В творчестве В.И. Арнольда огромную роль сыграло исследование тоже очень простой модели

                                                                               (4)

задающей отражение окружности ( – угол) в себя. Несмотря на удивительную внешнюю простоту, эта модель оказалась глубокой и содержательной.

По мнению Сергея Павловича, прикладная математика играет очень важную творческую роль в процессе познания. С одной стороны, исследование свойств нелинейных моделей даёт более глубокое понимание явлений в разных областях науки. Оно помогает «увидеть единое во многом».

С другой стороны, это исследование «подсказывает», где следует искать новые, пока неизвестные явления и сущности. Сергею Павловичу нравилась мысль выдающегося французского математика Анри Пуанкаре о будущем математики, в котором можно будет предсказывать и находить новое на основе анализа общей математической структуры теории, используемой в данной области. В большой степени компьютерное моделирование сделало эту мечту реальностью.

В основе нашего знания и способности разумно и дальновидно действовать лежит умение отделять основное от второстепенного. Но именно это и является главным при построения математических моделей! В ходе создания модели выделяются ключевые факторы и процессы, которые надо описать, и второстепенные, которыми можно пренебречь. Это гораздо больше, чем просто «язык», о котором любят говорить «теоретические математики». Ещё Галилео Галилей считал, что книга Природы написана языком математики. Сегодня мы можем добавить, что само содержание книги – математические модели, отражающие наиболее важные познанные причинно-следственные связи, характеризующие Природу, общество, человека.

Сергей Павлович предвидел, что математика XXI века будет очень сильно отличаться от той, что мы знаем сейчас. В самом деле, главными «заказчиками», «поставщиками задач» в ХХ веке были механика, физика, отчасти химия. Однако наступившее столетие, вероятно будет определять развитие наук о человеке и обществе. На авансцену выходят медицина, психология, социология, история, теория управления рисками, нейронаука, исследование различных сетевых структур. Они должны очень многое изменить и в прикладной математике, и в нашем понимании реальности.

В отличие от многих коллег, считающих, что математическое творчество – дело избранных, своеобразная «игра в бисер», доступная немногим, или своеобразный «спорт» Сергей Павлович представлял эту область исследований совершенно иначе. По его мысли – это сфера взаимодействия специалистов разного профиля, увлекательная попытка понять, что в разных областях науки является наиболее важным и общезначимым. По его мысли, идеи и понятия, рождающиеся в прикладной математике, становятся элементами культуры, а затем входят в массовое сознание.

И действительно, такие понятия как «точка бифуркации», «динамический хаос», «эффект бабочки», «режимы с обострением», пришедшие из прикладной математики, уже появились на страницах газет, в оценках экспертов, в речах политиков.

Сергей Павлович предвидел, что прикладная математика из дисциплины, «обслуживающей» другие области науки и сферы жизнедеятельности, станет, «генератором идей», основой междисциплинарных подходов. И на наших глазах этот прогноз сбывается.

Время и необратимость. На пороге новой революции в физике

Время всё ещё остаётся большой загадкой. Оно для нас не
более, чем общее понятие; мы не знаем даже, существует ли оно.

К. Саймак

Сергей Павлович заканчивал физический факультет Московского государственного университета и делал дипломную работу, посвященную теории атомного ядра, под руководством академика М.А. Маркова. Сформировавшийся у него в этом время физический стиль мышления, глубокое понимание значения законов природы он пронёс через всю жизнь.

Сергей Павлович считал своими учителями и относился с глубоким уважением и благодарностью к основоположнику вычислительного эксперимента академику Александру Андреевичу Самарскому и выдающемуся специалисту в области прикладной математики – асимптотического анализа, теории вычислительных алгоритмов, теории некорректных задач – академику Андрею Николаевичу Тихонову (которого он сменил на посту директора ИПМ). Важной вехой в истории Института, да и всей советской науки, стали расчёты ядерных устройств. Первая советская атомная бомба благодаря огромной физической интуиции, очень удачным математическим моделям и алгоритмам вычислений была рассчитана на логарифмических линейках. Однако совершенствование оружия требовало объёма расчётов, далеко выходящих за пределы возможностей одного специалиста и даже бригады расчетчиков – нужны были вычислительные машины, компьютерные модели и новое поколение алгоритмов.

Когда А.Н. Тихонов на одном из совещаний рассказал о принципиальной возможности провести прямые численные расчёты ядерных взрывов, выдающийся физик Л.Д. Ландау назвал такую работу «научным подвигом». И этот подвиг был совершён в отделе, которым руководил академик А.А. Самарский. Одним из активных участников всех этих работ был Сергей Павлович. Он мало рассказывал о том времени, хотя ясно осознавал, что главные задачи Института были решены именно тогда.

По мнению А.А. Самарского, причиной успешной конкуренции, несмотря на отставание в вычислительной технике, с командой американских исследователей, занимавшейся аналогичными задачами, состояла в том, что ядро американской команды составили математики, а советской – физики. Они глубже понимали сущность описываемых процессов и приближения, которые могут быть сделаны при моделировании.

Кроме того, мир уравнений в частных производных, с помощью которых описываются законы природы, очень сильно отличается от «дискретного», «цифрового», в котором работают вычислительные машины. Это разные сущности. Второй мир гораздо беднее, и надо тщательно взвесить, как и какие свойства исходных уравнений следует передать на дискретном уровне. И физики обычно понимают это лучше. Не случайно одним из наиболее развитых разделов компьютерного эксперимента является вычислительная физика.

В физической науке Сергея Павловича волновала проблема стрелы времени, необратимости физических, химических, биологических, социальных процессов.

В судьбе учёного очень важно время, в которое он живет, основное течение научной мысли, или, как сейчас говорят на западный манер, «мейнстрим».

Вспомним уравнение Ньютона

                                                                         (5)

Его следствием является сохранение энергии Е, представляющей сумму кинетической и потенциальной энергий. Кроме того, оно независимо (инвариантно) относительно смены знака времени t → -t. Это означает, что если уравнения Ньютона описывают пулю, вылетающую из ружья, или падающий и разбивающийся стакан, то с таким же успехом этому уравнению удовлетворяет и пуля, влетающая в ружьё, и стакан «впрыгиващий» на стол. Однако мы почему-то не видим ни того, ни другого. Откуда же берется эта необратимость.

В школе объясняют, что всё дело в диссипативных (рассеивающих энергию) процессах, переводяших её в более низкоорганизованную форму. Среди них трение, вязкость, теплопроводность, диффузия, электрическое сопротивление.

Вместе с тем в самых фундаментальных уравнения, как например, в уравнении Ньютона (5) или Шредингера

                                                                                                                                               (6)

диссипации нет. Она возникает на другом уровне, при описании взаимодействия многих частиц.

Уравнения, в которых сохраняется энергия, так называемые гамильтоновы системы, были в центре внимания в прикладной математике с 1970-х годов. Это уравнение Кортевега-де-Вриза

u_t = uu_x + u_xxx = 0

или кубическое уравнение Шредингера

iφ_t = Δ φ +| φ |² φ ,

которые имеют бесконечно много законов сохранения. В силу этого их решения во многих отношениях ведут себя как частицы.

Модные сейчас квантовые вычисления также происходят с помощью гамильтоновых, обратимых систем.

Сергей Павлович в этом отношении шёл против течения. Именно в необратимости он видел непонятое и непознанное свойство времени. Он считал, что эта необратимость должна содержаться на самом глубоком уровне материи, который описывают фундаментальные теории.

Во время нашей первой встречи я – тогда третьекурсник физфака – и Сергей Павлович – ведущий научный сотрудник – часа четыре ходили по скверу на Миусской площади. Мы говорили обо всём на свете, вновь и вновь возвращаясь к проблеме времени. Он посоветовал мне множество философских трудов, связанных со временем, которые «хотя и не доходят до уровня моделей, но хотя бы содержат размышления об этих сущностях».

Мысль о важности времени в его необратимой ипостаси возникла у него ещё в школе. В течение всей жизни он возвращался к идеям древнегреческого философа Гераклита Эфесского (544–475 г. до н.э.) и любил повторять его фразу: «Мир не создан никем из богов и никем из людей, а всегда был, есть и будет вечно живым огнём, мерами воспламеняющимся и мерами угасающим». Очень долгие годы изображение огня был на сайте С.П. Курюмова https://spkurdyumov.ru, который ведет В.С. Курдюмов и который стал одним из крупнейших порталов России.

Здесь две главные доминанты научной судьбы Сергея Павловича. Первая – огонь, необратимые процессы, которые, по его мысли, и являются основой ткани мироздания. Вторая – самоорганизация. Сергей Павлович был атеистом. Но это мировоззрение требует объяснения, как же возникла вся эта удивительная и прекрасная сложность мира, начиная от элементарных частиц и большого взрыва и кончая человеком, сознанием, обществом.

Мировое признание Сергею Павловичу и его научной школе принесло исследование модели тепловых структур

                            (7)

Это уравнение описывает процесс распространения тепла в горящей среде, в которой и коэффициент теплопроводности, и интенсивность источника являются нелинейными функциями температуры. Первоначально это уравнение возникло как часть модели, описывающей быстрые, нелинейные процессы в плазме. Однако Сергей Павлович пришёл к выводу, что оно заслуживает отдельного, специального изучения, и не ошибся. Решение этого уравнения обладают многими необычными для классической математической физики свойствами.

Во-первых, во многих случаях решения этого уравнения существуют конечное время – растут в режиме с обострением

Во-вторых, в широком классе начальных данных они стремятся при t → -t_f и автомодельным (самоподобным) решениям вида

где определяет закон роста амплитуды, φ (t) – полуширины, а функция  задает форму профиля температуры.

В-третьих, при β > σ + 1 эти решения оказываются пространственно локализованы. Их можно рассматривать как структуры, возникающие в нелинейной горящей среде. Поскольку диссипативные процессы (которые описывает член div (T^σ grad T) играют в их формировании принципиальную роль, Сергей Павлович назвал их нестационарными диссипативными структурами.

В-четвёртых, был обнаружен большой класс таких структур, представляющих собой сходящиеся к центру волны горения, в котором может быть множество максимумов, минимумов, слоёв. В достаточно простом уравнении открылся целый мир.

В-пятых, в простейшем «линеаризованном» случае уравнение для функции f совпало с уравнением Шредингера для атома водорода (точнее, для его «пространственной части»). Естественно возник вопрос, нельзя ли интерпретировать атом как структуру горящей среды.

В одном нелинейном уравнении открылось огромное пространство возможностей. О замечательных математических методах и результатах, полученных при его исследовании, тоже можно рассказывать подробно и интересно.

В Институте любили Сергея Павловича за его энергию, оптимизм, доброжелательность, умение организовать коллектив единомышленников, за справедливость и принципиальность. В течение многих лет он был секретарем парткома Института, а затем был избран его директором. Нашим первым директором был М.В. Келдыш, вторым – А.Н. Тихонов, третьим – Сергей Павлович.

Вместе с тем, работу по глубокому исследованию модели тепловых структур и режимов с обострением в Институте не всегда ценили и поддерживали. Академик А.Н. Тихонов советовал Сергею Павловичу взяться за более сложные и реалистичные модели, академик А.А. Самарский настаивал на том, что следует заниматься вычислительной математикой. Выдающийся физик, один из создателей советского ядерного оружия, академик Я.Б. Зельдович говорил, что Природа любит гамильтоновы системы. Сергей Павлович, относящийся с глубоким уважением к этим людям, шёл своим путём. Иногда отвечал: «Сегодня мы подтаскиваем математический аппарат для будущих физических теорий. И скоро всё это понадобится».

Иногда говорят, что исследователи являются сотрудниками единого «незримого колледжа», и единомышленниками могут оказаться учёные, работающие на другом конце планеты. Для Сергея Павловича большой поддержкой оказались работы выдающегося бельгийского ученого, лауреата Нобелевской премии по химии (1977) Ильи Романовича Пригожина. Их объединяло не только исследование диссипативных структур, но и создание нового научного мировоззрения.

По сути, есть три картины физической реальности. В первой, восходящей к Ньютону, мир предстает огромным часовым механизмом, созданным и запущенным Богом. И цель учёных состоит в том, чтобы постичь замысел этого творения. Этой идее следовал Эйнштейн, превратив время просто в одну из координат в своём описании пространства – времени. Этот идеал, к которых стремится большинство современных физиков, известный специалист по космологии Стивен Хокинг выразил в следующих словах: «Если мы действительно откроем полную теорию, то со временем её основные принципы станут доступны пониманию каждого, а не только нескольким специалистам. И тогда все мы, философы, учёные и просто обычные люди, сможем принять участие в дискуссии о том, почему так произошло, что существуем мы и существует Вселенная. И если будет найден ответ на такой вопрос, это будет триумфом человеческого разума, ибо тогда нам станет понятен замысел Бога».

Другая выдающаяся физическая теория – квантовая механика – имеет двойственную природу. На уровне описания объектов микромира мы вновь имеем дело с гамильтоновыми системами и эрмитовыми операторами. Но это описание определяет не само состояние квантового объекта, а вероятность найти его в том или ином положении в результате измерения. Необратимость создает процедура измерения, в результате которого из множества возможностей выбирается одна. Модель же «измерителя» и его свойства при этом обычно выносится за скобки. Вместе с тем само поле возможностей чётко очерчено. Нового не возникает. Времени вновь нет.

И, конечно, эта ситуация, имеющая мало общего с тем, что мы видим в мире, вызывает неудовлетворенность. Выдающийся математик и физик-теоретик Роджер Пенроуз выразил её в таких словах: «Я убежден, что наше современное представление о физической реальности – особенно в том, что касается природы времени – нуждается в коренном пересмотре, пожалуй, даже в более радикальном, чем тот, который был вызван к жизни современной теорией относительности и квантовой механикой.»[8]

Путь к новому пониманию времени сам Роджер Пенроуз связывал с пока не созданной квантовой теорией гравитации. Илья Пригожин, в конечном итоге, приходил к несамосопряжённым квантовомеханическим операторам, описывающим системы, в которых будущее отличается от прошлого.

Сергей Павлович полагал, что ответ даст теория самоорганизации и нелинейная динамика. В самом деле, развитие и в теории эволюции, и в биологии, и в истории всё чаще трактуется как прохождение последовательности бифуркаций. При этом выбор, зачастую случайный, сделанный на одном уровне организации материи, может определить законы, действующие на другом. Мир не является ньютоновским часовым механизмом, он – здание, которое недостроено, система в процессе своего творения, и мы иногда можем выступать не в качестве пассивных наблюдателей, а в роли его творцов. Акт творения возникает в результате разрешения тех или иных противоречий. И это очень близко к гераклитовскому мировидению.

Предчувствие будущей революции физики, как это обычно бывает, возникает и у писателей, поэтов, философов: «Отрицание временной последовательности, отрицание себя, отрицание астрономической Вселенной – всё это акты отчаяния и тайного сожаления. Время – это река, уносящая меня, но я сам река; это тигр, пожирающий меня, но я сам тигр; это огонь, поглощающий меня, но я сам огонь». Эти строки выдающиеся писателя Хорхе Луиса Борхеса были очень близки Сергею Павловичу. Он сам зажигал огонь, освещающий путь в будущее.

Синергетика в гуманитарном измерении

Тот, кто не хочет прибегать к новым средствам, должен ожидать новых бед.

Ф. Бекон

В 1950-х годах английский писатель и физик Чарльз Сноу с тревогой писал о растущей пропасти между двумя культурами – естественнонаучной и гуманитарной. Первая опирается на эксперимент и формализованные теории. Она устремлена в будущее, отвечает на вопрос «Как?» и игнорирует авторитеты, стремясь к объективности. Вторая в большой степени обращена в прошлое, опирается на традицию, принимает во внимание мнение известных лиц. Она должна отвечать на вопросы о целях, стратегиях, должном, допустимом и желательном, на вопрос «Что?».

Очевидно, средства, созданные благодаря стремительно растущим возможностям естественных наук, употребляемые в неверных целях, могут представлять огромную опасность. С другой стороны, провал гуманитарных дисциплин, не умеющих или не желающих заглядывать в будущее, не менее фатален. Нельзя в сегодняшнем или, тем более, в завтрашнем дне исходить из картины мира, относящейся ко вчерашним реалиям. Мир меняется очень быстро и существенно.

Сергей Павлович считал, что именно синергетика и междисциплинарные подходы дадут тот общий язык, на котором естественники, гуманитарии, математики, эксперты, руководители смогут обсуждать свои проблемы, полученные результаты, ставить задачи и рассматривать наиболее вероятные последствия принимаемых решений. Он думал, что именно синергетика станет мостом, переброшенным над пропастью двух культур.

Немецкий физик-теоретик Герман Хакен, предложивший термин «синергетика» вкладывал в него тот же смысл.

С одной стороны, этот подход рассматривает появление новых свойств и качеств у сложных систем, части или элементы которых такими свойствами не обладают.

С другой стороны, это подход, развитие которого требует совместных творческих усилий и взаимодействия естественников, математиков, гуманитариев, инженеров, управленцев.

Почти полвека развития синергетики показали, что достигнутые успехи пока представляются достаточно скромными. Активность и желание взаимодействовать со стороны естественников и математиков многократно превышают готовность и желание гуманитариев сотрудничать.

В схожей ситуации развития совместной деятельности математиков и биологов, где так же не всё шло поначалу гладко, сотрудник ИПМ, выдающийся математик и основоположник математической медицины, академик И.М. Гельфанд говорил: «Главная проблема в том, что математики не знаю математику, а биологи – биологию».

Возможно, сдвиги в сознании научного сообщества происходят достаточно медленно, и пока просто прошло слишком мало времени. Как говорил Сергей Павлович: «Будьте готовы к тому, что работу, которую вы написали сегодня, прочтут, поймут и оценят лет через десять, а то и позже».

Но, наверно, главная причина в том, что и гуманитарии, и математики, и естественники остро ощущают преимущество своего стиля мышления и восприятия мира и поэтому не готовы всерьёз учиться иному, вставать на другую точку зрения, вести на равных содержательный диалог. Это общее правило. Но Сергей Павлович относился к счастливым исключениям.

На первых курсах, во время учёбы на физическом факультете МГУ у него был план перейти на философский факультет университета, чтобы разобраться с самыми общими вопросами познания и бытия. Большой удачей стало то, что в деканате этого факультета ему попался мудрый человек. Он посоветовал сначала стать физиком, а потом браться за всё остальное. И если интерес к философии не пропадёт, то этими проблемами можно будет заниматься позже.

Интерес не пропал. Просматривая список научных трудов Сергея Павловича, в котором более 500 названий, видишь, что существенная часть работ в нем оказалась посвящена гуманитарной проблематике. Более 10 учеников Сергея Павловича стали докторами физико-математических наук, а Елена Князева – философских. Тиражи его книг, посвященных философским проблемам, намного превышают тиражи его работ по прикладной математике.

С.П. Курдюмов считал, что в ходе работы на острие научных проблем ХХ века в Институте возникли новое знание, понимание и мировоззрение, значение которых далеко выходит за пределы уже решенных задач, и очень важно было бы сделать всё это достижением всего общества.

В философии он видел способ сделать понятое элементом культуры. «Надо вовлечь друзей, коллег, гуманитариев в тот замечательный театр идей», – который мы увидели. И сам Сергей Павлович занимался этим с огромной энергией и энтузиазмом. Он читал лекции школьникам и академикам, профессорам и студентам. За последнее десятилетие своего творческого пути он прочёл более сотни лекций на конференциях, которые организовала ассоциация «Женщины в науке и образовании», возглавляемая Галиной Юрьевной Ризниченко. Он был очень увлекающимся лектором и готов был превысить временной лимит, отведенный ему на выступление, многократно – были бы слушатели.

Кроме преподавания на Физтехе он вел несколько курсов в Дубне, в университете «Природа, общество, человек», созданном Евгенией Наумовной Черемисиной – человеком огромной энергии, способностей и доброжелательности. Там его с восхищением слушали сотни человек. «Мне нравятся большие аудитории. Всегда думаешь, что из многих несколько человек воспримут наши идеи и либо воплотят в жизнь, либо понесут дальше, в будущее».