Назначение когнитивных сетей во многом остается непонятным. Можно предположить, что подобно безмасштабным функциональным сетям мозга, поддерживающим моторную кору в критическом состоянии, сеть языка поддерживает в критическом состоянии соответствующие области мозга человека. В таком случае возникает закономерный вопрос: если мозг человека эволюционировал из мозга животных для реализации языкового общения, то зачем мозгу человека необходима еще музыка, живопись, поэзия, художественная литература? Можно предположить, что для повышения своего репродуктивного успеха человек должен достичь как можно более высокого социального статуса в своей социальной группе, а поэзия, литература, живопись, музыка являются способами повышения социального статуса. Однако, по-видимому, это не единственная и даже не главная причина существования искусства. Мозг человека обладает свойством креативности (способностью создавать новое) не только в сфере искусства, но и в сфере технологий и науки. С точки зрения физики это может означать его возможность нахождения в сверхкритическом состоянии, которое, по-видимому, не свойственно мозгу животных (животные не обладают креативностью). Можно предположить, что когнитивные сети, связанные с произведениями искусства, поддерживают мозг в сверхкритическом стоянии и тем самым повышают его креативный потенциал.
Введение
Cложные сети принято разделять на технологические (Интернет, WWW), социальные (сети знакомств, сети сотрудничества) и биологические (экологические, функциональные сети мозга, сети белковых взаимодействий, метаболические сети) [2,3]. Закон распределения узлов по числу связей во всех перечисленных сетях описывается формулой ![]() , где q 0 и q 1 – константы, которая отражает явления насыщения при малых значениях q , и обрезания (cut-off) при больших значениях q . Такие сети получили название безмасштабных сетей (scale-free networks) [3,13,14]. При этом технологические и биологические сети отличаются от социальных сетей характером корреляции узлов, который получил название ассортативность. Показатель ассортативности описывается коэффициентом Пирсона:
, где q 0 и q 1 – константы, которая отражает явления насыщения при малых значениях q , и обрезания (cut-off) при больших значениях q . Такие сети получили название безмасштабных сетей (scale-free networks) [3,13,14]. При этом технологические и биологические сети отличаются от социальных сетей характером корреляции узлов, который получил название ассортативность. Показатель ассортативности описывается коэффициентом Пирсона:
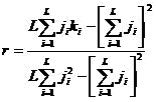
Здесь L число связей в сети, а j i и k i – число связей у узлов на обоих концах связи i . Если узлы с большим числом связей (хабы) связаны друг с другом, то r![]() 1 . Если узлы с большим числом связей связаны с узлами с небольшим числом связей, то r
1 . Если узлы с большим числом связей связаны с узлами с небольшим числом связей, то r ![]() -1 . Для технологических и биологических сетей свойственна отрицательная ассортативность [19], в социальных сетях имеет место положительная ассортативность, что является следствием фундаментального свойства социальных систем – гомофилии (homophily): потребностью человека образовывать связи и общаться с другими похожими на него людьми. Примером может служить «явление элитарного клуба» [1]. На языке теории сетей это означает, что узлы с наибольшим числом связей связаны между собой.
-1 . Для технологических и биологических сетей свойственна отрицательная ассортативность [19], в социальных сетях имеет место положительная ассортативность, что является следствием фундаментального свойства социальных систем – гомофилии (homophily): потребностью человека образовывать связи и общаться с другими похожими на него людьми. Примером может служить «явление элитарного клуба» [1]. На языке теории сетей это означает, что узлы с наибольшим числом связей связаны между собой.
В последнее время структурные свойства языка, тексты литературных произведений и тексты, связанные с религиозным сознанием (мифы Древней Греции, Ветхий и Новый Завет), а также организацию музыкальных произведений и живописи также стали изучать с точки зрения сетевого подхода[ ]. Очевидно, что соответствующие сети нельзя отнести ни к одной из трех вышеназванных категорий (технологические, биологические, социальные). Они образуют особую малоизученную категорию, которую мы будем называть когнитивными сетями.
Понятие «когнитивные сети» было предложено для сетевой структуры естественного языка [5] и это понятие естественно расширить на сетевые модели продуктов художественного творчества, а также текстов, связанных с религиозным сознанием. * Эти сети полностью или частично хранятся в памяти людей, более того, именно такого рода сети, отражающие связи слов, музыкальных звуков и т.п. участвуют в формировании той области сознания человека, которая отличает его от животных.
Предварительные исследования показывают, что когнитивные сети являются безмасштабными, однако, другие их свойства, в том числе показатель их ассортативности, во многих случаях не вычислялись. В данной статье мы рассмотрим сетевую модель языка, некоторых произведений литературы, музыки и живописи и обсудим некоторые пути исследований в этой области.
Сетевая структура языка
Р.Феррер-и-Канчо (Ramon Ferrer-i-Kancho) и Р.Соле (Ricard Sole) первыми построили сетевые структуры современного разговорного и письменного английского языка (Word Web), содержащего примерно 470 000 слов в качестве узлов сети, используя несколько правил соединения узлов [14]. Например, два слова (узла) связаны, если они встречаются в одном из предложений какого-либо текста. Фактически такого рода сеть и ее статистические свойства показывают вероятность совместного появления слов в осмысленных предложениях данного языка.
Полученная эмпирическая закономерность распределения вероятности узлов с данным числом связей в логарифмических координатах состоит из двух прямых линий разного наклона. Для письменного языка область ниже точки пересечения этих прямых подчиняется степенному закону с показателем степени ![]()
![]() 1.5, а для области выше точки пересечения – показатель степени равен
1.5, а для области выше точки пересечения – показатель степени равен ![]()
![]() 2.7, а коэффициент кластеризации, в зависимости от способа определения наличия связи между словами, находится в диапазоне C
2.7, а коэффициент кластеризации, в зависимости от способа определения наличия связи между словами, находится в диапазоне C ![]() 0.7 – 0.4, что более чем на три порядка выше, чем для соответствующих классических случайных графов. Такая сеть обладает свойством «тесного мира» [5] со средним межузловым расстоянием ‹ l ›
0.7 – 0.4, что более чем на три порядка выше, чем для соответствующих классических случайных графов. Такая сеть обладает свойством «тесного мира» [5] со средним межузловым расстоянием ‹ l › ![]() 2.65. Короткий путь есть отличительный признак эффективности передачи информации, которое отсутствует при болезни Альцгеймера, когда этот путь имеет существенно большую длину.
2.65. Короткий путь есть отличительный признак эффективности передачи информации, которое отсутствует при болезни Альцгеймера, когда этот путь имеет существенно большую длину.
___________________
* В англоязычной научной литературе термин «cognitive networks» используется также в исследованиях по адаптации технических устройств к окружающей технологической среде и это направление также перспективно для понимания когнитивных функций мозга человека (см., например, Cognitive Networks. Edited by Q. Mahmoud. John Wiley& Sons Ltd. 2007)
Сети персонажей
На протяжении трех тысяч лет писатели, поэты, художники, композиторы используют в своем творчестве мифологические образы древней Греции. Возможно, и сейчас эти сюжеты и образы формируют нас не в меньшей степени, чем современная литература.
Словарь классической греческой мифологии Гранта и Хазеля содержит биографии всех персонажей древнегреческих мифов, как всем известных богов, так и малоизвестных нимф [7]. Всего в словаре 1647 богов, нимф, чудовищ, сирен, простых смертных. На основе этого словаря была сконструирована ориентированная сеть межличностных связей героев древнегреческих мифов [17]. В этой сети каждому узлу соответствует определенный персонаж, а узлы А и В соединены связью, если в при описании персонажа А появляется персонаж В и наоборот. Сконструированная таким образом ориентированная сеть оказалась безмасштабной с ? out ![]() 3.0 и ? in
3.0 и ? in ![]() 2.5. Среднее число шагов между узлами в этой сети равняется _ l _
2.5. Среднее число шагов между узлами в этой сети равняется _ l _ ![]() 3.47. Зависимость коэффициента кластеризации от степени узла в построенной сети подчиняется степенному закону с показателем степени, равным 0.63, что указывает на то, что сеть имеет иерархическую структуру. К сожалению, в указанной публикации не содержится значение показателя ассортативности.
3.47. Зависимость коэффициента кластеризации от степени узла в построенной сети подчиняется степенному закону с показателем степени, равным 0.63, что указывает на то, что сеть имеет иерархическую структуру. К сожалению, в указанной публикации не содержится значение показателя ассортативности.
Подобного рода новые подходы в исследовании канонических текстов религиозных учений очень важны для когнитивной науки, поскольку религиозное сознание было первой формой сознания человека, и понимание закономерностей различных аспектов его формирования может помочь в изучении других форм сознания, в том числе связанного с искусством.
В отличие от мифологических произведений, взаимодействие персонажей Нового Завета в определенной степени отражает реальные исторические события, и по этой причине можно было бы ожидать, что соответствующие социальные взаимодействия формирует сеть c положительной ассортативностью. Однако, оценка ассортативности и коэффициента кластеризации эгоцентричной сети взаимоотношений Иисуса с другими 79 персонажами Нового Завета [New Testament Social Network, 2007] дает значения -0.133 и 0.74 соответственно. Эту сеть также следует отнести к когнитивным сетям, поскольку ее структура (или ее отдельные фрагменты) хранится в памяти миллионов людей.
Д.Стиллер (James Stiller), Д. Неттл (Daniel Nettle) и Р.Данбар (Robin Dunbar) исследовали структуры взаимодействия персонажей в десяти наиболее популярных пьесах В.Шекспира. Каждый персонаж пьесы является узлом соответствующей сети. Два узла такой сети связаны между собой, если соответствующие персонажи хотя бы раз одновременно появлялись на сцене [16].
Анализ построенных сетей для всех десяти пьес показал, что герои связаны друг с другом не более чем двумя степенями разделения, а социальные связи в этих пьесах имеют высокую степень кластеризации. Увеличение числа персонажей в пьесах Шекспира ведет к росту числа социальных групп, по мере того как драма увеличивается в размерах, коммуникативные связи становятся менее насыщенными.
Обычно общее число персонажей в пьесах Шекспира варьирует в пределах 30-40, что сравнимо с размерами древних охотничьих сообществ и числом социальных контактов человека в современном обществе. Возможно, эта величина соответствует тем пределам когнитивных способностей человека, за которыми уже становится затруднительным отслеживание всех возможных изменений в структуре социальных контактов [16], что согласуется с числом Данбара (Dunbar Number) равным 150.
Персонажи литературных романов образуют сети друзей и знакомых, поэтому естественно предположить, что такие сетевые структуры являются социальными сетями. В Таблице 1 представлены данные по числу персонажей и показателю ассортативности пяти известных литературных произведений. Как мы видим, ни одну их сетевых структур взаимосвязи персонажей этих произведений по характеру корреляции узлов нельзя отнести к социальным сетям.
Таблица 1. Сравнительные характеристики сетевых структур персонажей некоторых произведений мировой литературы
|
Author and title |
Число персонажей |
Ассортативность r |
Кластеризация C |
| Л.Н.Толстой “Анна Каренина” |
138 |
-0.350 |
0.65 |
| Ч. Диккенс “Давид Копперфилд” |
87 |
-0.258 |
0.69 |
| М.Твен “Геккельберри Финн” |
74 |
-0.173 |
0.77 |
| Гомер “Илиада” |
561 |
-0.118 |
0.40 |
| В.Гюго “Отверженные” |
80 |
-0.165 |
0.55 |
В заключение этого раздела, упомянем работу П.Гляйзера из Аргентины (Pablo Gleiser of the Centro Atomico Bariloche in Argentina) [4], который исследовал сетевую структуру героев комиксов, в которой два узла (два персонажа) связаны между собой, если они появляются и взаимодействуют друг с другом в одной книге комиксов. В полученной таким образом сети коэффициент ассортативности также оказался отрицательным [ ].
Литература и поэзия как сложные сети
Мазуччи (A.Masucci) и Роджерс (C.Rodgers) построили сеть семантических связей слов в романе Дж.Оруэла «1984» по мере их появления в тексте [11]. Эта сеть оказалась безмасштабной, однако ассортативность этой сети не вычислялась. Аналогичным образом можно построить сетевую структуру поэтического текста: в качестве узлов брать отдельные слова этого текста, включая предлоги и местоимения, а два узла соединяются направленной связью от соответствующего слова в тексте к следующему за ним в данном тексте слову. Такой метод ничем не отличается от используемого при анализе прозы [ ], а получаемую этим методом сеть поэтического текста можно сравнить с сетью его дословного перевода на иностранный язык.
Чтобы учесть ритмическую структуру стихотворения и наличие в нем рифмы мы, соответственно, соединяем два ближайших слова связью, если эти слова содержат ударные слоги, а также соединяем связью два слова на концах двух ближайших строк, если у этих слов имеется рифма. Рисунок 1 показывает образовавшуюся сеть для стихотворения А.С.Пушкина ”Брожу ли я вдоль улиц шумных…”.
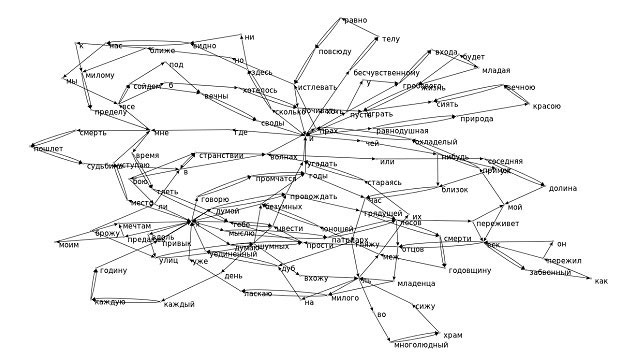
Рисунок 1. Мультиграф стихотворении А.С.Пушкина “Брожу ли я вдоль улиц шумных…” с учетом ритмических и рифмических связей между словами
Статистические показатели этой сети следующие: L=8.215, C=0.079, ?=1.442, r=0.0629
Разумеется, такой подход исследования ритмической и рифмической организации поэтического текста является довольно грубым и отражает лишь примитивное восприятие поэзии. Мы планируем провести исследование поэтического текста на уровне слогов и морфем, что, возможно, позволит выявить более тонкие свойства поэзии.
Безмасштабные сети музыкальных произведений
Партитура музыкального произведения легко преобразуется в сетевую структуру, если в качестве узлов такой сети взять музыкальные ноты всех возможных длительностей. Нетрудно подсчитать, что число узлов для одного голоса в такой сети не будет превышать 1800. В самом деле, число клавишей у рояля равно 88 и, умножая это число на 20 – число длительностей ноты (половинные, четверти, восьмые и т.д.), получаем 1760. Связи между узлами (нотами) в сети устанавливаются по хронологическому принципу: если нота I начинает звучать в момент времени T , а нота J в этот момент заканчивает свое звучание, то между соответствующими узлами сети имеет место связь.
Ли (Xiaofan Liu), Тсе (Chi K. Tse) и Смол (Michael Small) из политехнического университета Гонконга проанализировали статистические свойства сетей, построенных по описанному выше принципу, для произведений Баха, Моцарта, Шопена и современных китайских композитов, работающих в жанре поп музыки. Все эти сети оказались безмасштабными [9]. Среднее число шагов между узлами в этих сетях варьируют в диапазоне от 2.8 до 4.2. Другие параметры сетей также изменялись довольно значительно для различных произведений.
Нами были построены ориентированные сетевые структуры для всех четырех частей сочинения Бетховена «Большая фуга си-бемоль мажор» для струнного квартета опус 133». Узлами сети, как и в описанном выше исследовании, брались отдельные ноты различных длительностей, а узлы соединялись стрелкой в направлении от предшествующей ноты к последующей. На рисунке 2 показан фрагмент сети для первой скрипки четвертой части этого сочинения.
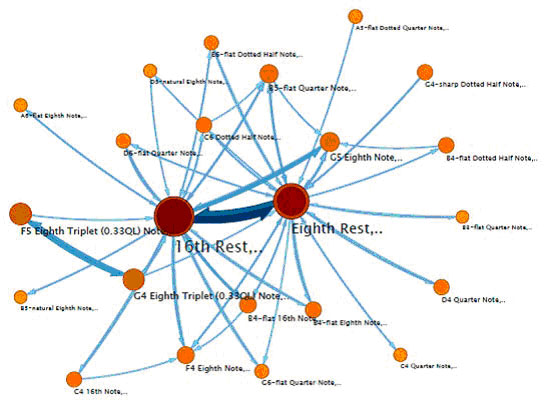
Рисунок 2. Фрагмент сети для первой скрипки четвертой части сочинения Л.Бетховена «Большая фуга си-бемоль мажор» для струнного квартета опус 133.
Показатель степени этой безмасштабной сети равен ? ![]() 1.13. В данный момент мы проводим исследование, в котором учитывается тональная, ритмическая и гармоническая структуры музыкального произведения.
1.13. В данный момент мы проводим исследование, в котором учитывается тональная, ритмическая и гармоническая структуры музыкального произведения.
О сетевой структуре некоторых произведений кубизма
В статье [8] показано, что при случайном разбиении плоскости на непересекающиеся смежные блоки, можно построить безмасштабную сеть, в которой узлами будут сами блоки, а связями – общая граница между блоками. В живописи кубистов (Пикассо, Брак, Мондриан и др.) такими блоками чаще всего являются треугольники, квадраты и прямоугольники, но можно найти и другие геометрические и негеометрические формы. На Рисунке 3 представлена картина П.Пикассо «Портрет» и ее сетевая модель.
 |
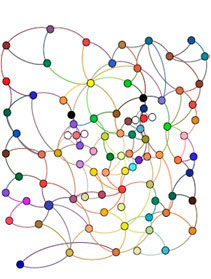 |
Рисунок 3. Портрет П.Пикассо а) и его сетевая структура б)
Закон распределения узлов по числу связей можно записать в виде: P ![]() q -2.43 , коэффициент кластеризации С=0.343, среднее межузловое расстояние 4.53
q -2.43 , коэффициент кластеризации С=0.343, среднее межузловое расстояние 4.53
Рассмотрим одну из картин голландского художника-кубиста Пита Мондриана (1892-1944) (Рисунок 4)
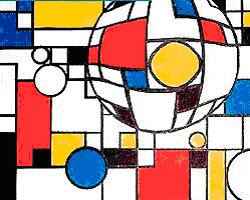
Рисунок 4. Пит Мондриан. Композиция.
Распределение узлов по степеням для сети этой картины подчиняется степенному закону ![]() , Показатель степени для сети этой картины равен ?
, Показатель степени для сети этой картины равен ? ![]() 3.2. Коэффициент кластеризации этой сети C
3.2. Коэффициент кластеризации этой сети C ![]() 0 .2, а среднее межузловое растояние ‹ l ›
0 .2, а среднее межузловое растояние ‹ l › ![]() 3.2 [18].
3.2 [18].
Картина русского художника Казимира Малевича (1878-1935) “Лесоруб” принадлежащая к живописному стилю “кубофутуризм”, также легко разбивается на непересекающиеся блоки (Рисунок 5).

Рисунок 5. К.Малевич. Дровосек
Соответствующая сетевая структура также является безмасштабной с ? ![]() 1.94, коэффициентом кластеризации C
1.94, коэффициентом кластеризации C ![]() 0 .37 , и ‹ l ›
0 .37 , и ‹ l › ![]() 4.1.
4.1.
Подход, описанный здесь, может быть обобщен, если разбивать плоскость картины на области, имеющие один цвет. В этом случае можно исследовать гораздо большее число живописных стилей.
Заключение
Назначение когнитивных сетей во многом остается непонятным. Можно предположить, что подобно безмасштабным функциональным сетям мозга, поддерживающим моторную кору в критическом состоянии [21], сеть языка поддерживает в критическом состоянии соответствующие области мозга человека.
В таком случае возникает закономерный вопрос: если мозг человека эволюционировал из мозга животных для реализации языкового общения, то зачем мозгу человека необходима еще музыка, живопись, поэзия, художественная литература? Можно предположить, что для повышения своего репродуктивного успеха человек должен достичь как можно более высокого социального статуса в своей социальной группе, а поэзия, литература, живопись, музыка являются способами повышения социального статуса. Однако, по-видимому, это не единственная и даже не главная причина существования искусства.
Мозг человека обладает свойством креативности (способностью создавать новое) не только в сфере искусства, но и в сфере технологий и науки. С точки зрения физики это может означать его возможность нахождения в сверхкритическом состоянии [3], которое, по-видимому, не свойственно мозгу животных (животные не обладают креативностью). Можно предположить, что когнитивные сети, связанные с произведениями искусства, поддерживают мозг в сверхкритическом стоянии и тем самым повышают его креативный потенциал.
Литература
- Bak P. How Nature works. Copernicus. New York, 1997
- Caldarelli G. Scale-Free Networks. Complex Webs in Nature and Technology. Cambridge University Press. 2007
- D.R. Chialvo. Are our senses critical? Nature Physics 2, 301–302 (2006).
- Ferrer I Cancho R. and Sole R. Small world of human language. 2001. Proc.Royal Soc. B. 268, 2261
- Gleiser, P. M. preprint http://arxiv.org/abs/0708.2410 (2007).
- Grant, M. and Hazel, Z. Gods and Mortals in Classical Mythology: A Dictionary, Dorset Press, 1985.
- Eguiluz, V. M, Chialvo, D. R. , Cecchi, G, Baliki, and Apkarian, V.// Physical Review Letters. -2005 . –v . 94. – 018102
- Hassan, M.K., Hassan, M.Z. and Pavel N.I. Scale-free network topology and multifractality in a weighted planar stochastic lattice. New Journal of Physics, 12 (2010) 093045
- Liu, X. , Tse, C., Small,. M., Complex network structure of musical compositions: Algorithmic generation of appealing music. Physica A 389 (2010) 126 – 132
- Masucci A.P. and Rodgers G.J. Network properties of written human language. Physical Review E 74, 026102 (2006)
- Newman M. E. J., 2003, Mixing patterns in networks. // Phys. Rev. E 67 , 026126, arXiv:cond-mat/0209450
- Newman M. Networks. An Introduction. Oxford University Press, 2010
- Sole R, Corominas-Murtra S B. Valverde, and Steels L. Language Networks: Their Structure, Function, and Evolution. Complexity, 2010
- Sporns O. Networks of the Brain. The MIT Press. 2011.
- Stiller J., l Nettle D. and Dunbar R.. The Small World of Shakespeare’s Plays. Human Nature, vol.14, N 4, 2003, pp.379-408
- Yeon-Mu Choi and Hyun-Joo Kim. A Directed Network of Greek and Roman Mythology. Physica A 382 (2007) 665–671
- Yevin I. and Shuvalov N. The Theory of Complex Networks in Painting Studying. Unifying Themes in Complex Systems. Volume VIII. Proceedings of the Eighth International Conference on Complex Systems New England Complex Systems Institute. Book Series NECSI Knowledge Press., Editors: Hiroki Sayama, Ali A. Minai, Dan Braha, Yaneer Bar-Yam, p. 751
- M. E. J. Newman and Juyong Park, Why social networks are different from other types of networks , Phys. Rev. E 68 , 036122 (2003).
- M. E. J. Newman Ego-centered networks and the ripple effect , , Social Networks 25 , 83–95 (2003).
- D. E. Knuth, The Stanford GraphBase: A Platform for Combinatorial Computing , Addison-Wesley, Reading, MA (1993).
- Egu??luz V. M., Chialvo D. R, Cecchi G. A, Baliki M., and Apkarian A.V. Scale-Free Brain Functional Networks . PRL 94, 018102 (2005)
- R. Alberich , J. Miro-Julia , F. Rossello . Marvel Universe looks almost like a real social network. preprinthttp://xxx.arxiv.org/abs/cond-mat/0202174 (2002).
