ВВЕДЕНИЕ
В последние годы теория сложных сетей стала новым эффективным инструментом изучения многих сложных систем, когда модель системы представляется в виде сети взаимодействующих между собой ее элементов [7, 13]. Образованная таким образом сетевая структура представляет собой своеобразный каркас соответствующей сложной системы, что позволяет изучать свойства всей системы в целом и преодолевать многие недостатки других подходов, пытающихся свести поведение всей целостной системы к анализу отдельных ее элементов или частей. Между тем, существуют сложные системы, в которых взаимодействия между их элементами могут иметь качественно различную природу. Наглядным примером может служить система общественного транспорта мегаполиса. Остановки общественного транспорта в городе, которые обычно берутся в качестве узлов сети, могут быть связаны различными видами транспорта: автобусом, трамваем, троллейбусом и метро. Для моделирования таких систем развивается математический аппарат теории многослойных сетей, в котором каждый сетевой слой описывает связи между узлами одной природы [5]. В данном примере строятся отдельно сеть метро, сети автобусов, троллейбусов, трамваев, связи между ними и изучаются свойства этой многослойной сетевой структуры. Физические и структурные свойства многослойных сетевых моделей сложных систем существенно (иногда радикально) отличаются от свойств их однослойных аналогов, поэтому изучение многослойных сетей позволяет более адекватно понять саму природу моделируемых систем [5]. Цель данной статьи — показать, что произведения таких видов искусства как литература и музыка, также допускает моделирование в виде многослойных сетей.
МОДЕЛЬ ПОЭТИЧЕСКОГО ПРОИЗВЕДЕНИЯ
Покажем на примере стихотворения А.С. Пушкина «Я Вас любил…» возможный подход к построению многослойной сетевой модели. На рисунке 1 представлена семантическая сеть этого поэтического шедевра. Смысловые связи между словами показаны самым простым способом — по мере их появления в тексте стихотворения (если два слова стоят рядом в тексте, то между ними существует смысловая связь) [8].
Рис. 1. Семантическая сеть стихотворения А.С. Пушкина «Я Вас любил…» представляет собой первый слой его многослойной структуры.
В задачу данной статьи не входит расчет отдельных количественных характеристик сетевого слоев данного стихотворения. Сравнения показателей и параметров сетевых структур различных поэтических текстов (диаметр сетей, коэффициент кластеризации, корреляционные свойства сетей, законы распределения узлов по числу связей, анализ спектральных свойств матриц смежности и т.д.) должны стать темой специальных исследований [10].
В качестве второго слоя поэтического произведения можно взять сетевую структуру, описывающую его ритмическую организацию. На рисунке 2 изображена сеть тех слов этого стихотворения, на которые падает ударение.
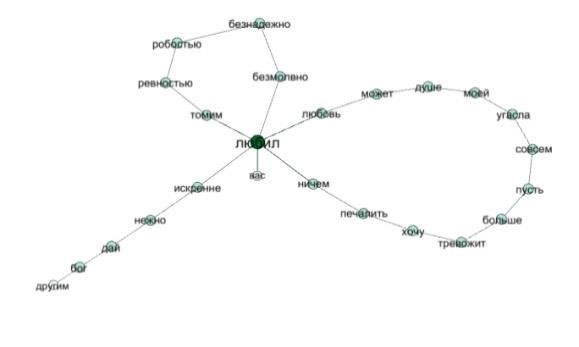Рис. 2. Слова, на которые падает ударение в стихотворении « Я Вас любил…», образуют еще один сетевой слой.
Сравнительный анализ сетевых структур, описывающих ритмические свойства различных поэтических произведений и видов поэтического творчества – тема специальных исследований. Кроме того, отметим на возможность построения еще одного слоя, описывающего рифмические связи между словами в тексте данного стихотворения. Этот слой изображен на рисунке 3.
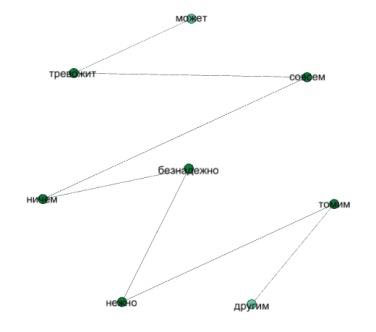Рис. 3. Рифмические связи в стихотворении А.С. Пушкина «Я Вас любил..»
СЕТЕВАЯ МОДЕЛЬ ХУДОЖЕСТВЕННОЙ ПРОЗЫ
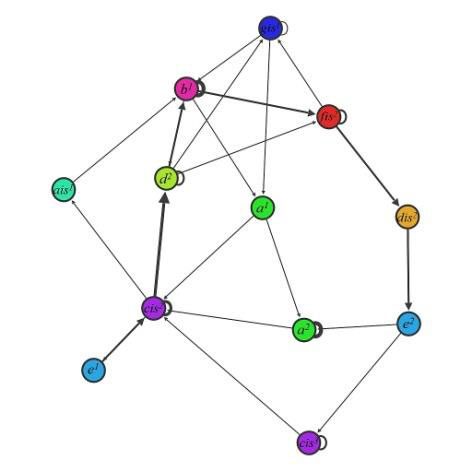
Обратимся теперь к литературной прозе. На рисунке 4 показана семантическая сеть первых пятидесяти слов романа Л.Н. Толстого «Анна Каренина». В работе [12] на примере романа Дж. Оруэлла «1984» даны возможные направления изучения такого рода семантических сетевых структур.
Рис. 4. Семантическая сеть первых пятидесяти слов романа Л.Н. Толстого «Анна Каренина»
В статье [9] представлены некоторые результаты изучения количественных закономерностей эволюции такого рода лингвистических сетей. В частности, обнаружена зависимость среднего кратчайшего расстояния между словами от размера сетей по мере их роста и предложена математическая модель такой эволюции.
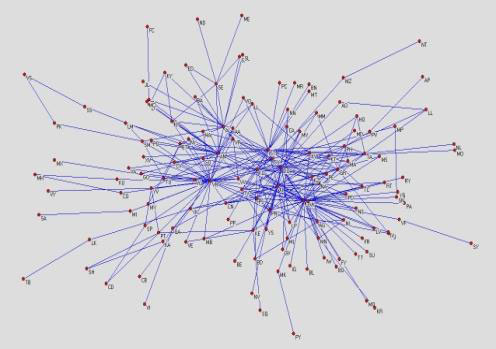
Мы в данной работе укажем на возможность изучения еще одного сетевого слоя этого романа – сети его персонажей (рис. 5). Проведенные нами исследования сети персонажей этого и некоторых других произведений мировой литературы показали довольно неожиданный результат – сети героев литературных романов не образуют социальные сети, поскольку обладают свойством диссортативности (их коэффициенты корреляции имеют отрицательное значение) [1 ,2].
Рис. 5. Сеть 125 персонажей романа Л.Н. Толстого «Анна Каренина».
МОДЕЛЬ МУЗЫКАЛЬНОГО ПРОИЗВЕДЕНИЯ
Обратимся теперь к музыке. Мелодия любого музыкального произведения легко преобразуется в сетевую структуру, если в качестве узлов такой сети взять музыкальные ноты всех возможных длительностей. Нетрудно подсчитать, что число узлов для одного голоса в такой сети не будет превышать 1800. В самом деле, число клавишей у рояля равно 88 и, умножая это число на 20 – число длительностей ноты (половинные, четверти, восьмые и т.д.), получаем 1760. Связи между узлами (нотами) в сети устанавливаются по хронологическому принципу: если нота I начинает звучать в момент времени T, а нота J в этот момент заканчивает свое звучание, то между соответствующими узлами сети имеет место связь, направленная от J к I.
Ли (Xiaofan Liu), Тсе (Chi K. Tse) и Смол (Michael Small) из политехнического университета Гонконга проанализировали статистические свойства ориентированных сетей, построенных по описанному выше принципу, для произведений Баха, Моцарта, Шопена и современных китайских композитов, работающих в жанре поп музыки. Все эти сети оказались безмасштабными [11]. Например, ноктюрн Ф.Шопена имеет суммарный показатель степени равный 1.4. Коэффициент ассортативности этих сетей принимает как положительные, так и отрицательные значения.
Любое звуковысотное движение, образующее мелодическую линию, представляет собой цепочку ладовых переходов со ступени на ступень лада. Отсюда каждую мелодию можно представить как последовательность таких переходов, в целом образующих сеть. Узлами сети будут являться звуки лада, связями – переходы между ними.
Сетевой подход к исследованию мелодии позволяет наглядно представить индивидуальную структуру мелодии, ее «внутреннюю жизнь». Так, особенностью мелодии прелюдии Ф. Шопена А-dur является преобладание в ней тонов “h”, “cis “, “a” (“хабы” в терминологии теории сетей). Они являются I, III и II ступенями лада соответственно. Динамику их взаимоотношений на границе первого и второго предложений периода можно представить в виде следующей схемы: II (такт 1 ) — III (такт 8) // II (такт 9) — I (такт 16).
Рис. 5. Сетевая модель мелодии прелюдии Ф. Шопена А-dur.
Сетевой подход возможен и в анализе гармонии данной прелюдии. Здесь хабами будут уже наиболее встречающиеся аккорды, а не отдельные звуки. Такими аккордами являются доминантовый септаккорд D7 и тоническое трезвучие Т3/5. Они заявлены в самом начале прелюдии – в тактах 1-2 и 3-4. Между мелодией и гармонией наблюдается статистическая корреляция: хабы в мелодии входят в хабы гармонии: звук “h” (II ступень) гармонизуется аккордом D7, а звуки “cis” (III) и “a” (I) – тоническим трезвучием Т3/5. Исключение – кульминация пьесы в тактах 12-13: здесь “h” становится местной тоникой. В этом фрагменте именно гармония «доопределяет», уточняет значения мелодических тонов, в частности, звука “cis”. Вот почему для полноты картины нужна вторая сеть (аккордика прелюдии).
Рис. 6. Сетевая структура аккордов прелюдии Ф. Шопена А-dur
Сеть мелодии и сеть аккордики музыкального произведения образуют специальный случай многослойных сетей – так называемые взаимозависимые сети [6], свойства которых в настоящее время интенсивно изучаются. В статье [1] нами предложен сетевой подход к изучению живописи кубистов, показывающий, что некоторые работы П. Мондриана и П. Пикассо можно описать в виде многослойных сетей. Вопрос, можно ли обобщить этот подход на другие направления живописи, а также скульптуру, архитектуру и т.д. требует дополнительных исследований.
ЗАКЛЮЧЕНИЕ
Можно предположить, что сама возможность описания произведений некоторых видов искусства в виде многослойных сетевых моделей есть следствие многослойной морфологической и функциональной сетевой организации структуры мозга человека [14] и поэтому изучение фундаментальных свойств многослойных сетевых структур произведений искусства может пролить свет на некоторые закономерности функционирования мозга.
Уровень нашего понимания сложных систем всегда связан с неполнотой информации об их структуре и свойствах. Количественной мерой неполноты информации о системе является ее энтропия. В последнее время в теории сложных сетей разрабатываются методы расчета энтропии как простых однослойных, так и многослойных сетей на основе расширения и обобщения наиболее важных понятий и методов статистической физики (канонический ансамбль, статистическая сумма и т.д.) [3, 4]. Можно ожидать, что приложение этих новых подходов к изучению произведений искусства и их взаимодействию с мозгом человека углубит наше понимание как природы искусства, так и принципов функционирования мозга.
Данная работа была поддержана Российским Гуманитарным Научным Фондом (заявка N 14-04-00369).
ЛИТЕРАТУРА
1. Евин И.А., Кобляков А.А., Савриков Д.В., Шувалов Н.Д. Когнитивные сети // Компьютерные исследования и моделирование. – 2011. – Т. 3, № 3. – С. 231–239.
2. Евин И.А., Хабибуллин Т.Ф. Социальные сети // Компьютерные исследования и моделирование. – 2012. –Т. 4, № 2. – С.423-430.
3. Anand K., Bianconi G, Severini S. Shannon and von Newman entropy of random networks with heterogeneous expected degree. Physical Review E, 2011, no. 83, 036109.
4. Bianconi G. Statistical mechanics of multiplex networks: Entropy and overlap. Physical Review E, 2014, no. 87, 062806.
5. Bocaletti S., Bianconi G., Criado R., del Genio C., Gomez-Gardenes J., Romance M., Sendina-Nadal I., Wang Z., Zanin M. Structure and Dynamics of Multilayer Networks. Physics Reports, 2014, vol. 544, no. 1, pp.1-122.
6. Buldyrev S., Parshani R., Paul G., Stanley H., Havlin Sh. Catastrophic cascade of failures in interdependent networks. Nature, 2010, 15 April, vol. 464, pp.1025-1028.
7. Caldarelli, G.: Scale-Free Networks: Complex Webs in Nature and Technology. Cambridge, Cambridge University Press, 2007, 324 p.
8. Ferrer-i-Cancho R., Sole R.V. The small world of human language. Proc. of The Royal Soc. of London. Series B, Biological Sciences, 2001, vol. 268 (1482), pp. 2261–2265.
9. Kulig A., Drozdz S., Kwapien J., Oswiecimka P. Modeling the average shortest-path length of word-adjacency networks. Physical Review E, 2015, no. 91, 032810.
10. Liang W., Wang Y., Shi Y., Chen G. Co-occurrence network analysis of Chinise and English poems. Physica A, 2015, no. 420, pp. 315-323.
11. Liu, X., Tse, C., Small, M. Complex network structure of musical compositions: Algorithmic generation of appealing music. Physica A, 2010, no. 389, 126–132.
12. Masucci, A.P., Rodgers, G.J. Network properties of written human language. Physical Review E, 2006, no. 4, 7026102.
13. Newman M.E.J.: Networks. An Introduction. Oxford, Oxford University Press, Oxford, 2010, 771 p. 14. Sporns O. Networks of the Brain. Cambridge, The MIT Press, 2011, 412 p.