Введение

В последнее  время    сложные системы  различной природы (технологические, биологические, социальные, когнитивные) стали представлять в виде сетевых структур [10-12].  Узлы в таких сетях представляют собой элементы этих сложных систем, а связи между узлами – взаимодействия между элементами. В данной работе исследуется  структурная сложность дорожной системы Москвы  в процессе ее  роста и эволюции. Для исследования  из Интернет-ресурсов были получены графы дорожных сетей трех районов города Москвы: в пределах Садового кольца (далее «Старая Москва»), Ленинского района Москвы (далее «Послевоенная Москва»), и  крупного района,  недавно присоединённой  к  Москве на юге (далее «Новая Москва»). Основным показателем,  определяющим  сложность  структуры дорожной сети, является коэффициент  сетчатости.

Данные для дорожных сетей берутся из открытых источников ресурса OpenStreetMap (OSM) – некоммерческого веб-картографического проекта по созданию подробной географической карты мира силами Интернет-сообщества. Сайт ресурса – http://www.openstreetmap.org/.  Выбор этого ресурса объясняется наличием уникальных идентификаторов перекрёстков и их связей друг с другом.

В ходе выполнения работы с помощью программного пакета JOSM (редактора карт OpenStreetMap) были загружены xml файлы с сервера OSM,  имеющие расширение .osm и описывающие структуру дорожной сети в выбранном при выгрузке квадрате. При выгрузке области любой формы используется несколько квадратных областей, полностью покрывающих нужную область с точностью до погрешности на границах.

Для конвертации полученных данных из файла формата .osm в вид дорожного графа  была реализована программа на языке программирования java, обрабатывающая данные XML. На выходе программа создаёт текстовый файл формата .txt со списком рёбер, каждое из которых имеет параметр: начальная вершина, конечная вершина, идентификационный номер.

Визуализация графа и вычисление основных характеристик производится в программе для анализа и визуализации сетей – Gephi 0.8.2. Программа в свою очередь принимает на вход текстовый файл .txt, данные из которого импортируются в базу данных рёбер, тем самым определяя и вершины графа.

В программе Gephi происходит расчёт основных показателей дорожного графа:

1. Количество вершин и рёбер графа – количество перекрёстков и участков дорог между перекрёстками выбранной области
2. Средняя степень графа
3. Коэффициент кластеризации
4. Коэффициент сетчатости – универсальная оценка сложности сети

Для расчёта этих коэффициентов была реализована программа на языке программирования Python. В ходе выполнения программы полученный ранее список ребер считывается из текстового файла и преобразуется в граф с помощью внутренней библиотеки NetworkX.

Во многих сложных сетях важным свойством является топология коротких циклов. Для этого необходимо оценивать количество циклов определённой длины:  треугольники (длина цикла L = 3), квадраты (регулярная сетка c L = 4) или в виде сот (L = 6). Для первого случая (L = 7) достаточно вычислять коэффициент кластеризации , который показывает количество треугольников в сети. Для более сложных циклов  коэффициент кластеризации будет давать нулевое значение для любого цикла с L ≠ 3. Поэтому в 2004-м году Джером Буль  ввёл понятие коэффициента «сетчатости» (meshedness coefficient), который позволяет оценить структуру сети с циклами произвольных длин [ 2].

Коэффициент сетчатости определяется по формуле M = F/F_max, где F – количество граней (без внешней грани) планарного графа с количеством вершин N и количеством рёбер K, которое может быть выражено через формулу Эйлера F = K — N + 1. F_max – это максимально возможное число граней в связном планарном графе с тем же количеством вершин N и, соответственно, количеством рёбер K_max= 3N — 6. (так как связный граф – это граф, в котором все вершины связаны). Таким образом, F_max = 2N — 5 и значение коэффициента сетчатости может принимать значение от нуля (древовидная структура) до единицы (связный граф). Значит, при увеличении коэффициента сетчатости, сложность структуры сети увеличивается.

Пример изменения коэффициента сетчатости от 0 до 1:

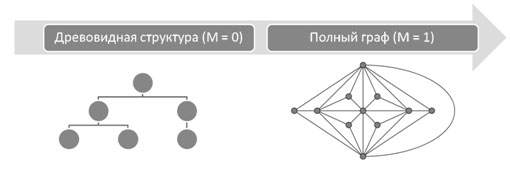
Рисунок 1. Визуализация коэффициента сетчатости

Данные, полученные с сервера OSM, реализованы в виде XML-документа и состоят из множества тегов <node> и <way> с набором атрибутов. Теги в качестве атрибутов содержат уникальный идентификатор (id) и GPS координаты каждой точки с  тегом <node>,  являющиеся элементом «пути”, обозначенным тегом <way>. Каждый “путь” описывает ломаную линию, проведенную последовательно через точки, список уникальный идентификаторов которых содержится в его атрибутах. Данная ломаная линия  описывает либо участок дорожной сети (в том числе пешеходные дороги), либо периметр здания. Наличие у “пути” тега с атрибутом k = ‘highway’, и v равным любому значению из второй колонки таблицы 3, является признаком, что данный тег <way> описывает автомобильную дорогу. Разрешенное направление движения задается тегом с атрибутом k=’oneway’ и v=’yes’ или v=’no’, в зависимости от наличия на данной дороге одностороннего движения. Также в значениях атрибутов каждого элемента, описывающего участок дороги, содержится информация о количестве полос для движения, типе дороги, названии улицы и др.

Таблица 1. Классификация дорог, изображённых на картах OpenStreetMap

Для получения дорожного графа на языке программирования java была написана программа, принимающая на вход xml файл описывающего структуру дорожной сети. В результате выполнения, данная программа записывает в текстовый файл список отрезков дорог, фрагмент полученного текстового файла показан на рисунке 2.

Рисунок 2. Пример данных в текстовом файле

Каждая строчка полученного файла содержит gps-координаты и уникальные идентификаторы точек, являющихся началом и концом данного отрезка; уникальные идентификаторы точек, обозначающих перекрестки, дорога между которыми содержит данный   отрезок; уникальный идентификатор дороги между перекрестками, то есть ребра дорожного графа; вес ребра, то есть расстояние в метрах между перекрестками по дороге; признак 0 или 1 в зависимости от того является движение на описываемой дороге односторонним (1 если дорога односторонняя). Строчки со 2 по 5 описывают ребро 1119, длинной 81.5 м, между перекрестками(вершинами графа) 1642801590 и 1189036523, состоящее из 4 отрезков задающихся внутренними точками 1642801583, 1642801582, 1642801581. Данное ребро является неориентированным, то есть движение разрешено в обе стороны.

Выбор геометрической области дорожной сети задаётся квадратом, имеющим 4 идентифицирующих координаты: максимальные и минимальные широту и долготу – Lat_max, Lat_min, Lon_max, Lon_min. В случае ограничения области для Новой Москвы выгрузка данных из OSM воспроизводилась 16-ю различными квадратами, поскольку, во-первых, размер области оказался слишком большим для одноразовой выгрузки – сервер ресурса неспособен выгружать такие объёмы данных обычным способом, во-вторых, границы области не имеют прямоугольной формы:

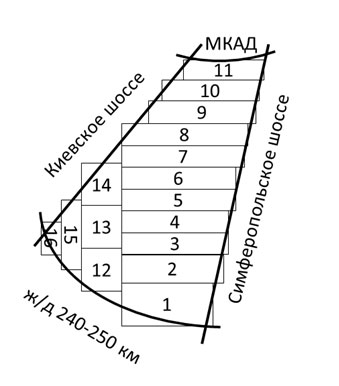
Рисунок 3. Схема по выбору границ области для района Новой Москвы

На рисунке отмечено 16 областей, выгрузка каждой из которых записывалась в файлы формата .osm.  Далее, каждый файл был преобразован в текстовый файл формата .txt, и уже в этом формате 16 файлов были объединены в единый файл формата .txt для импорта данных в программу визуализации графов Gephi.

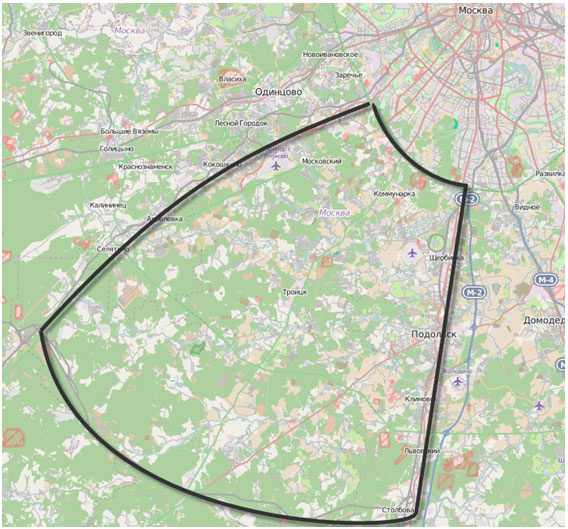Рисунок 4. Выделенный район Новой Москвы

Выделенный участок Новой Москвы характерен слабой застройкой по сравнению с остальными районами Москвы, что покажет отличие урбанизированных районов от районов, недавно бывших аграрными.

В отличие от большого и нестандартного участка Новой Москвы, районы Старой Москвы в пределах Садового кольца и Ленинского проспекта берутся единой прямоугольной областью, поскольку погрешности на границах от требуемых районов не превышают 10%, что не может серьёзно влиять на показатели сети, поскольку «приграничные участки» имеют схожую структуру.

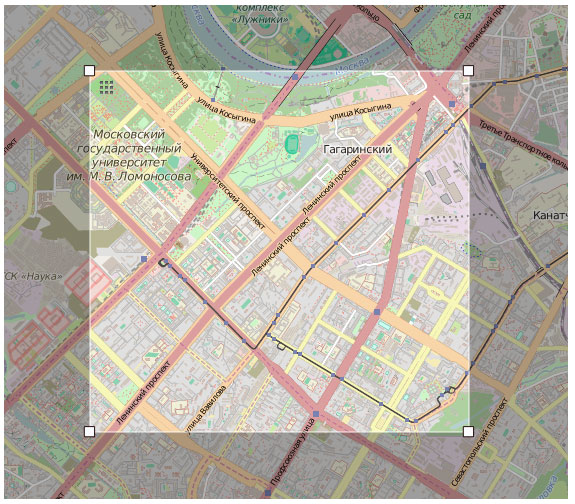
Рисунок 5. Выгруженный квадрат дорожной сети Ленинского района

Границы Ленинского района задаются следующими координатами:

Lat_max =  55.711;                    Lat_min = 55.676

Lon_max = 37.589;                    Lon_min = 37.524

Выделенный участок ограничен улицей Косыгина на севере, Московским университетом на западе, Нахимовским проспектом и ст. м. Профсоюзной на юге и проспектом 60-летия Октября на востоке. Этот участок характерен массовой застройкой и планированием улиц и кварталов в послевоенный период.

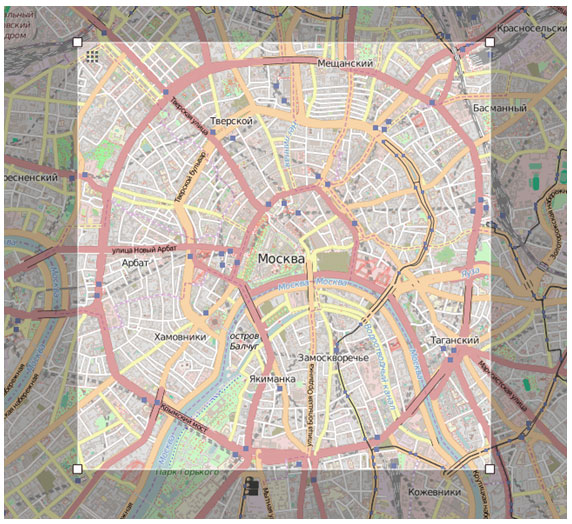Рисунок 5. Выгруженный квадрат дорожной сети внутри Садового кольца

Границы дорожной сети Москвы внутри Садового кольца задаются следующими координатами:

Lat_max =  55.776;                    Lat_min = 55.728

Lon_max = 37.660;                    Lon_min = 37.579

Выделенный участок характерен радиально-кольцевой структурой, причём застройка улиц и кварталов происходила путём самоорганизации с момента возникновения Москвы.

Алгоритм решения поставленной задачи можно разбить на несколько логических частей:

1. Извлечение данных из ресурса OSM в файл формата .osm
2. Конвертация данных из формата .osm в формат .txt с помощью программы на Java
3. Построение дорожного графа в программе Gephi и вычисление основных характеристик
4. Вычисление дополнительных характеристик с помощью надстройки над Gephi, реализованной на Python
5. Анализ полученных результатов

Построение дорожных графов и расчёт показателей производится в программе Gephi. Здесь приведена сводная таблица рассчитанных показателей:

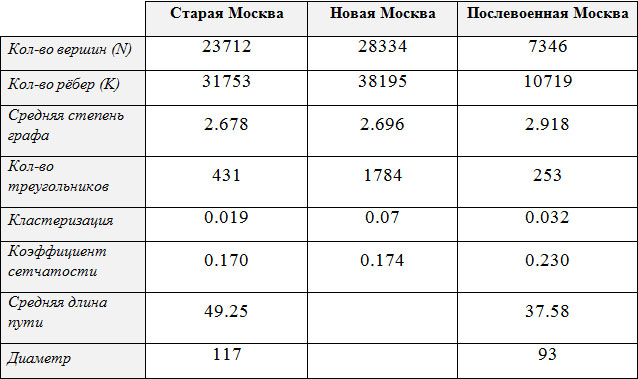
Таблица 2. Сводная таблица показателей трёх рассчитанных графов дорожной сети Москвы

2. Анализ полученных результатов

Полученные результаты хорошо соотносятся с подобными характеристиками дорожных сетей городов мира, что позволяет классифицировать сеть Москвы на разных этапах её эволюции: стихийная самоорганизация вокруг центра, этап активного планирования второй половины XX века, зарождающийся этап индустриализации окраины Москвы.

Классификация дорожной сети по этапам эволюции

Понятие этапов эволюции дорожной сети вводится в работе Э. Страно, В. Никосиа, В. Латора, С. Порта , М. Бартелеми –[1, 3-9 ] . В этой работе выделяется  четыре этапа:

1. Аграрный этап (Rural phase): базируется на аграрной экономике без наличия развитой транспортной инфраструктуры, преобладают просёлочные дороги
2. Ранняя урбанизация (Early-urban phase): строительство ж/д линий; строительство дорог вне исторического центра
3. Индустриальный этап (Urban-industrial phase): характерное индустриальное развитие (в особенности механика и текстиль), вследствие этого рост популяции, строительство автомагистралей
4. Постиндустриальный этап (Metropolitan post-industrial phase): развитие высокоскоростных поездов и крупной системы автомагистралей

В качестве примера рассматривается крупная  аграрную область Гроане немного севернее постиндустриального Милана, которая переживает рост своей дорожной сети. Анализ структуры Гроаны прекрасно соотносится с характеристиками Новой Москвы, поэтому данная работа может быть взята за основу в моделировании эволюции Новой Москвы до индустриального этапа.

Схожесть структур Гроаны и Новой Москвы при статическом рассмотрении (без учёта эволюции) определяется близостью средних степеней сетей: рост от 2,57 до 2,8 у Гроаны при 2,696 у Новой Москвы. Помимо средней степени берётся другой коэффициент r_N, вычисляемый по формуле

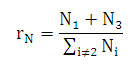
где N_i – есть количество узлов степени  (из рассмотрения убраны узлы степени 2, как не рассматриваемые в корректном определении перекрёстков).

Коэффициент  показывает относительное количество тупиков (относящихся к N₁) и перекрёстков Т-типа (относящихся к N₃) так, что малое значение коэффициента свидетельствует о превосходстве перекрёство степени i = 4, что, в свою очередь, ведёт к модели решётчатой структуры. Обратно, при коэффициенте r_N  близком к 1, сеть по большей части состоит из перекрёстков Т-типа и тупиков. Для ясности, этот коэффициент можно назвать коэффициентом аграрности рассматриваемой сети.

Для Гроаны r_N ≅ 0, 835, тогда как для Новой Москвы r_N ≅ 0, 825. Это позволяет заметить обилие перекрёстков степени i до 3, а значит, пока ещё аграрный этап развития сети.

Наконец, по графикам из работы  [1] можно оценить коэффициент сетчатости дорожной сети Гроаны в 2007-м году, имея оценку количества вершин N ≅ 5100, а количества рёбер K ≅ 7100 имеем коэффициент сетчатости K ≅ 0, 196. По данному показателю Гроана опережает Новую Москву, что свидетельтствует о более сложной структуре пригорода Милана, т.е. о наличии узлов с количеством связей, превышающих i = 3.

Сводная таблица параметров дорожных сетей городов мира:

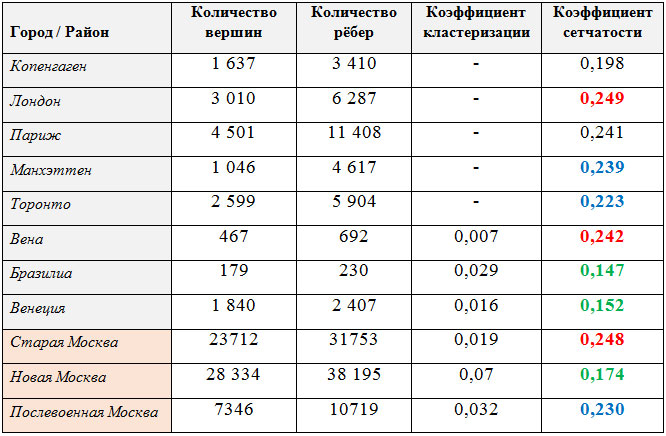
Таблица 4. Сводная таблица основных параметров сложности городов мира

Как видно из  Таблицы 4, центр Старой Москвы сравним по сложности с центрами Вены и Лондона, район Новой Москвы – с центрами Венеции и Бразилиа, а Ленинский район наиболее близок к центрам Торонто и Нью-Йорка (район Манхэттен).

ЛИТЕРАТУРА

[1]   Strano, E., Nicosia, V., Latora, V., Porta, S. & Bartheґlemy, M. Elementary processes governing the evolution of road networks. Sci. Rep. 2, 296; DOI:10.1038/srep00296 (2012).

[2]   J. Buhl, J. Gautrais, N. Reeves, R.V. Solé, S. Valverde, P. Kuntz, G. Theraulaz. Topological patterns in street networks of self-organized urban settlements. European Physical Journal B 49 (2006) 513

[3]   Jiang B, Duan Y, Lu F, Yang T, Zhao J. Topological structure of urban street networks from the perspective of degree correlations. 2014. Environment and Planning B: Planning and Design 41(5) 813 – 828

[4]   M. Barthelemy, A. Flammini. Modeling Urban Street Patterns. Physics Reviews Letters 100 (2008) 138702.

[5]   Barthelemy, M., Bordin, P., Berestycki, H., & Gribaudi, M. (2013). Self-organization versus top-down planning in the evolution of a city. Scientific reports, 3.

[6]   Abundo, C., Bodnar, T., Driscoll, J., Hatton, I., & Wright, J. (2013). City population dynamics and fractal transport networks. Proceedings of the Santa Fe Institute‘s CSSS2013.

[7]   A. Cardillo, S. Scellato, V. Latora, S. Porta. Structural properties of planar graphs of urban street patterns. Physical Review E 73 (2006) 066107

[8]   P. Crucitti, V. Latora, S. Porta. Centrality measures in spatial networks of urban streets. Physical Review E 73 (2006) 036125

[9]   P. Yuan, Z. Juan. Urban road network evolution mechanism. Physica A 392 (2013) 5186–5193

[10]  И.А. Евин. Введение в теорию сложных сетей. Компьютерные  исследования и моделирование. 2010, т2. №2, с. 121-141

[11]  Евин И.А., Кобляков А.А. ,  Савриков Д.В. , Шувалов Н.Д..  Когнитивные сети. Компьютерные исследования и моделирование. 2011. т. 3.  no.  3.  сс. 231–239.

[12] Евин И.А., Хабибуллин Т.Ф. Социальные сети. Компьютерные исследования и моделирование.  2012, v 4, no. 2,  сс.423-430