Введение

Представление улично-дорожных систем городов в виде сетей (графов) берет свое начало с известной работы Леонарда Эйлера 1736 года о семи мостах Кенигсберга, заложившей основы новой тогда математической дисциплины – теории графов. В последнее время методы этой теории успешно применяются в исследованиях по географии, урбанистике и других научных направлениях. Научный подход в изучении городских территорий, использующий теорию планарных графов для представления дорожной сети, в котором перекрестки городов являются узлами, а дороги – связями, получило название теория первичных графов (primary graph).

В данной работе мы будем исследовать дорожные сети  центра Москвы (Бульварное кольцо) и центр Петербурга, представляя их в виде двойственного графа (dual graph). В этом подходе названия улиц (то есть, сегменты дорог, имеющие названия) берутся в качестве узлов сети, а связи между узлами устанавливаются в том случае, если соответствующие улицы пересекаются. Отметим, что такое представление городской среды в последние годы широко используется в теории пространственного синтаксиса (space syntax) [1,4-6]. Двойственный граф называют также информационным графом, поскольку он содержит всю информацию, необходимую для перемещения по городу из одной его точки в любую другую (для навигации по городу). В этом случае  не нужно знать все названия улиц и всех площадей и  перекрестков, встречающиеся на   пути, а  нужно знать только названия тех улиц (узлов двойственного графа), на которых нужно менять направление, например, cделать поворот. Максимальная информация, которая необходима, чтобы пересечь весь город, равна диаметру двойственного графа дорожной сети города.

Представление дорожной сети города в виде двойственного графа стало отправной точкой исследований шведского физика — теоретика Мартина Розвалла (Martin Rosvall)  и его коллег по навигационным и информационным свойствам некоторых шведских городов (Стокгольм, Гетеборог, Мальме и Умен) и сравнение соответствующих показателей с дорожными сетями других городов мира [5,7-9].  Информационные показатели двойственных дорожных сетей городов, введенные в этих работах, дают количественную оценку трудности навигации путешественника, впервые приехавшего в город   и ищущего нужное ему место по его адресу. Эти показатели также оценивают количество информации, накапливающееся у путешественника при знакомстве с городом и даже разницу в   ощущениях при движении по некоторому маршруту туда и обратно. Первое путешествие по незнакомому маршруту всегда кажется более длительным, чем движение по этому же маршруту в обратном направлении.

В статье [8] рассмотрена задача оценки  сложности навигации по  городам с различным типом дорожных сетей в двойственном представлении. Для того, чтобы охарактеризовать  легкость  или же, наоборот, сложность навигации в дорожной сети   города, авторами используется переменная S (от searchability – разыскиваемость, находимость, доступность), которая отражает общее количество информации, необходимой для нахождения (достижения) нужного места в городе.

Допустим, мы хотим найти кратчайший  маршрут с улицы s на улицу t (или с одного узла  информационного (двойственного)  графа на другой.. Если кратчайших путей больше одного (вырожденность), то выбирается любой из них. По предварительной оценке, количество информации, требуемой для  выбора нужного выхода с узла, степень которого k, есть log₂(k).  Для каждого найденного пути от узла s до узла t вероятность выбора этого маршрута в качестве самого оптимального представлена формулой:

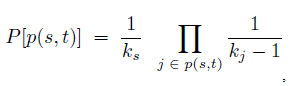
в которой переменная j проходит по всем узлам, затрагиваемым в маршруте, до ближайшего к t.

Общая вероятность найти узел t среди всех вырожденных кратчайших путей есть

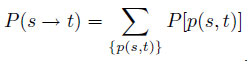
Общая «информационная сложность» навигации  или  «доступность» по любому из кратчайших маршрутов есть

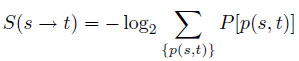
В работе [2]  введено понятие  предельной когнитивной сложности навигации в транспортных сетях города различной природы (улично-дорожных, сетях метрополитена, автобусов и т.п.). Это понятие введено по аналогии  с известным «числом Данбара» [3], характеризующим предельные когнитивные возможности человека поддерживать дружеские связи в социальных сетях. Британский антрополог Робин Данбар в своих исследованиях показал, что максимальное число  знакомых, с которыми человек способен поддерживать  достаточно тесные дружеские связи не превышает 150 человек. В статье [2] показано, что максимальная информационная сложность двойственного графа для достаточно простой навигации по нему не должна превышать 8.1 бит.

Основные результаты

В нашей  работе были применены описанные выше формулы и алгоритмы к двойственному графу, построенного на основе дорог и их пересечений, которые лежат в пределах Бульварного кольца Москвы (Рисунок 1). Заметим, что  в этом районе присутствуют дороги и с одно- и с двусторонним движениями; дороги с ограничением проезда для автотранспортных средств; ограничения поворотов и другими свойствами. Однако целью данной работы, как писалось выше, являлся анализ представленного района в плане доступности адресов улиц (узлов). Поэтому при построении двойственного графа исследуемого района не принимались во внимание описанная различия в типах дорог: то есть, построенный двойственный граф является неориентированным.

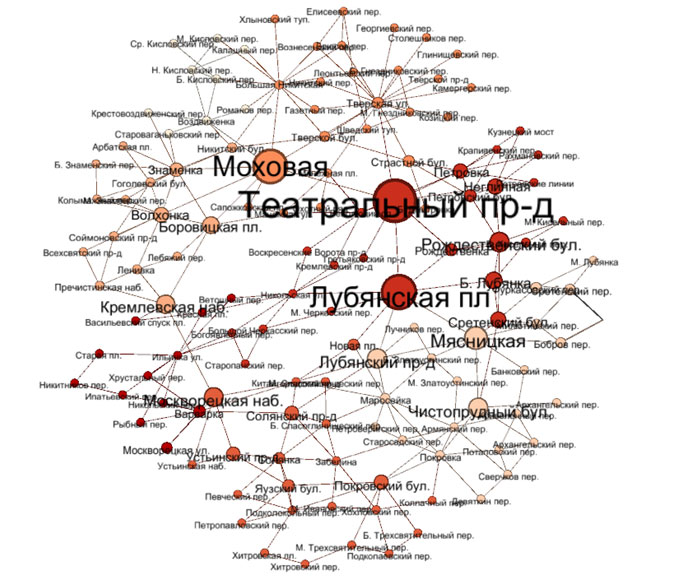
Рисунок 1.  Двойственное представление дорожной сети  Бульварного кольца Москвы. Узлы ранжированы по загруженности данной дороги (betweenness centrality).  Численно он равен количеству кратчайших путей, проходящих через дорогу между двумя любыми вершинами графа, деленному на общее число кратчайших путей в этом графе.

Аналогичный двойственный граф был построен для центрального района Петербурга. Сравнение навигации по дорожным сетям центров Москвы и Петербурга интересно потому, что их развитие  происходило по двум различным сценариям: самоорганизации и централизованного планирования соответственно.

Для района Бульварного кольца Москвы  распределение числа улиц по их загруженности (betweenness centrality)  имеет следующий вид:

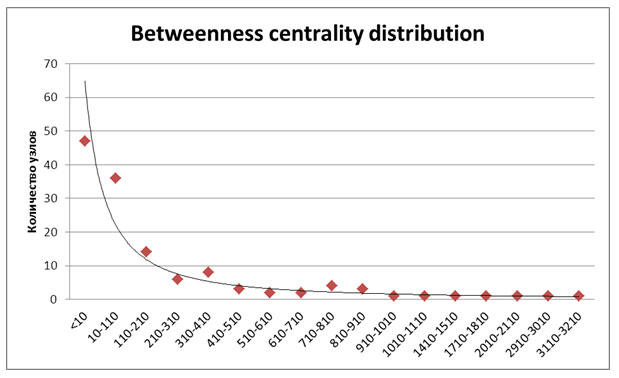
Как и ожидалось,  это распределение описывается степенным законом с показателем степени равным 2.1. Согласно этому закону, больше всего узлов с маленькими значениями betweenness centrality – то есть улицы, по которым редко ходят; и только пара улиц, играющих важную роль в городском трафике. Наибольшие значения betweenness centrality в зоне Бульварного кольца Москвы показывают Театральный проезд, Лубянская площадь и улица Моховая:

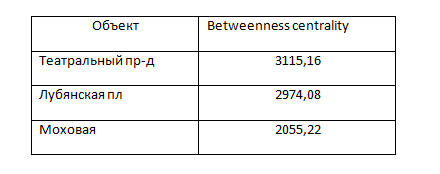
Closeness centrality

Еще одной характеристикой узла графа служит closeness centrality – среднее длина пути от данного узла до всех остальных узлов в графе.

При рассмотрении Бульварного кольца, распределение следующее:

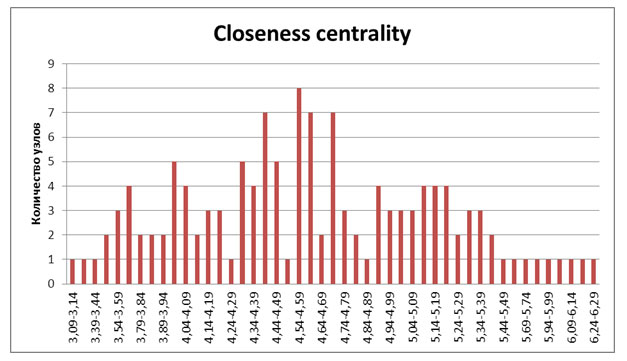
Searchability и связь с Closeness centrality

Выше уже упоминалось о  такой характеристике, как searchability (доступность), которая показывает, какое необходимо количество информации, чтобы из узла s дойти в узел t. После программного подсчета по всем парам узлов дя графа, построенного на основе дорожной сети Бульварного кольца Москвы, получилось, что среднее значение searchability равно  9,6 бит информации, что превышает когнитивный порог навигации в 8.1 бит [2], о котором говорилось выше.

Доступность нахождения t при навигации из s напрямую зависит от количества промежуточных узлов. Как известно,  мера closeness centrality отражает среднее расстояние (количество узлов) от узла до остальных узлов. Рассмотрим, есть ли связь между этими двумя  показателями.

Closeness centrality – это характеристика одного узла, в то время как доступность – характеристика пары узлов. Для того, чтобы нивелировать данное несоответствие, прибегнем к следующему приему: возьмем для каждого узла его среднюю доступность среди всех пар между данным узлом и другими узлами

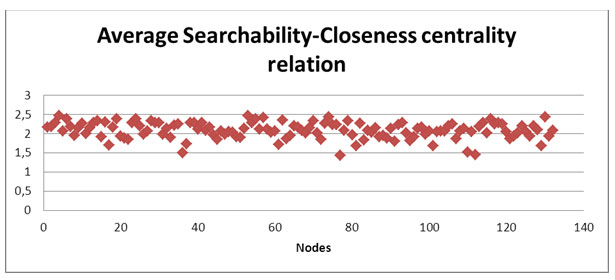
На графике видна явная корреляция между двумя сравниваемыми характеристиками. Значение средней доступность узла в среднем в два раза больше его closeness centrality.

На Рисунке 2 покан  граф дорожной сети центра Петербурга в двойственном  представлении.

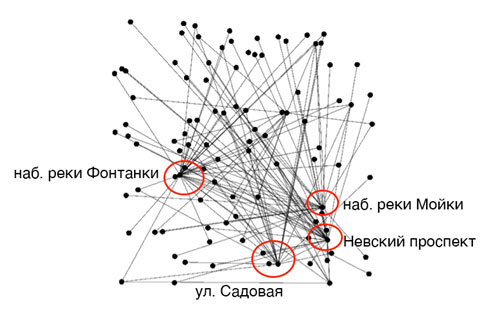
Рисунок 2. Двойственный  граф дорожной сети  центра Санкт-Петербурга

Проведенные нами программные расчеты «доступности» (searchability) для дорожной сети центра Петербурга в двойственном представлении,  дали среднее значение 7,4 , что  ниже порогового значения когнитивной загруженности при навигации [2].

Диаметр D графа определяется как наибольшее расстояние между двумя вершинами в графе. Диаметр графа дорожной сети  центра Петербурга в двойственном представлении равен 5, что меньше диаметра аналогичного графа для центра Москвы равный 12. Это  еще одно свидетельство того, что для навигации по Петербургу требуется меньше информации, чем для навигации по Москве.

Дорожные сети центра Петербурга и Москвы   в двойственном представлении являются безмасштабными сетями, описываемой степенным законом распределения вершин по числу связей, где показатель степени равны 2,6 и 2.8 соответственно.

Список литературы

1. Blanchard P., Volchenkov D. Mathematical Analysis of Urban Spatial Networks. Springer-Verlag, Berlin, Heidelberg,  2009
2. Galliotti R.,  Porta M., Barthelemy M.. Information measures and cognitive limits in multilayer navigation.  ArXiv 1506.01978v.1 5 Jun 2015
3. Dunbar R. How many friends does one person need? Harvard University Press, Cambridge, 2010
4. Masucci P., StanilovK., and  Batty M. Exploring the evolution of London’s street network in the information space: A dual approach. Physical Review E 89, 012805 (2014)
5. Rosvall,M . Grönlund, P. Minnhagenand K. Sneppen. Searchability of networks. Physical review Е 72, 046117 (2005), DOI: 10.1103.
6. Portugali J. Complexity, Cognition and the City. Springer, Berlin,  2011
7. K. Sneppen, A. Trusina and M. Rosvall. Hide-and-seek on complex networks. Europhysics Letters –  2005, DOI: 10.1209
8. K. Sneppen, A. Trusina, P. Minnhangen and M. Rosvall. Networks and Cities: An Information Perspective. Physical review letters, 2005,  028701
9. K. Sneppen, A. Trusina and M. Rosvall. Communication boundaries in Networks. Physical review letters, 2005, PRL 94, 238701 (2005)