Евин И.А., Букашев А.А.,Марченко Д.К.

Московский физико-технический институт (государственный университет)

Федеральное государственное бюджетное учреждение науки

Институт машиноведения им. А.А.Благонравова

Российской академии наук

Введение

В истории человечества урбанизация представляет собой процесс фундаментальной важности, влияющий как на свойства самого человеческого сообщества, так и на окружающую  его природную  среду. Первые города возникли более 5000 лет назад и именно в них возникли  и стали развиваться наука и технологии, определившие  все дальнейшее развитие человечества. Доля городских жителей уже достигла 50% от всей численности населения Земли и  продолжает увеличиваться. Каждую неделю население всех городов мира увеличивается приблизительно на один миллион человек, а суммарная площадь этих городов к 2030 году превысит площадь Франции, Германии и Испании вместе взятых. Многие возникающие при этом проблемы (рост социального неравенства, преступности, загрязнения окружающей среды и другие) диктуют необходимость  научиться управлять процессами урбанизации, выстраивая соответствующие долговременные стратегии экономического развития государства, а для этого необходимо, прежде всего, выявить и понять основные качественные и количественные закономерности процесса урбанизации.

Проблемам городов, их развития и эволюции посвящено огромное количество публикаций, включающих, в том числе, количественные методы исследования и моделирования  (см. например, [1-4]). В последние годы в связи с возникновением нового метода изучения сложных систем – теории сложных сетей[5-7]  стали появляться работы, в которых городские территории, прежде всего сети дорог и коммуникаций, описываются и изучаются методами этого нового перспективного научного направления[8-9].

Основные понятия теории сложных сетей

Матрица смежности описывает все свойства сети Элементы матрицы смежности a_ij = 1 если узлы i и j сети соединены  друг с другом и 0 в противоположном случае [6]

Среднее наименьшее расстояние между всеми узлами сети (диаметр сети)  , где d_ij — наименьшее расстояние между узлами i и j.

Коэффициент кластеризации 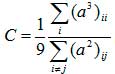, характеризующий наличие в сети циклов длины три[6].

Большинство реальных сетевых структур можно описать небольшим числом параметров, отличающих их от случайных графов и регулярных решеток:

1. Небольшая величина среднего расстояния между узлами и высокими значениями коэффициента кластеризации
2. Степенной закон распределения узлов сети по числу принадлежащим им связям.
3. Наличие сообществ и мотивов   в структуре  реальных сетей.

Такие сети получили название безмасштабных или  сложных сетей

Дорожные сети принадлежат к особому классу сложных сетей – пространственным сетям. Эти сети встроены в двухмерное или трехмерное евклидово пространство, а связи между узлами представляют собой реальные физические соединения, в отличие, например, от  связей в сетях сотрудничества актеров кино или ученых. Примерами пространственных сетей могут служить нейронные  сети мозга, сети электростанций, сети общественного транспорта (автобусные, троллейбусные, метро) и т.п.

В данном обзоре мы рассмотрим вопросы моделирования частного случая  пространственных сетей – дорожных (уличных) сетей городов. Топология этих сетей, как и других видов пространственных сетей, накладывает определенные ограничения на их свойства. Ясно, например, что длина связей между узлами в дорожных сетях сильно влияет на их стоимость, что, разумеется, ограничивает проявление такого свойства сложных сетей как свойство «тесного мира».

показатель важности дорожной сети[8].

Локальные свойства дорожных сетей городов

При изучении локальных свойств  дорожных  сетей городов, используются следующие понятия  теории планарных графов:

Минимальное остовное дерево (minimum spanning tree MST)  дерево кратчайшей длины, соединяющее все исходные узлы.

Триангуляция – планарный граф, все внутренние области которого являются треугольниками.

  жадная триангуляция (greedy triangulation GT) алгоритм, генерирующий список всех возможных отрезков, соединяющих пары исходных точек, и он сортируется по длине отрезков. Начиная с самого короткого, последовательно выполняется вставка отрезков в  триангуляцию. Если отрезок не пересекается с другими ранее вставленными отрезками, то он вставляется, иначе он отбрасывается. Получающийся планарный граф имеет максимально возможное число связей при минимальной длине самого графа[8].

Коэффициент Meshedness

M представляет собой обобщение показателя   циклической структуры сети (коэффициент кластеризации)

Коэффициент сетчатости (Meshedness coefficient M)

Во многих сложных сетях важным свойством является топология коротких циклов. Для этого необходимо оценивать количество циклов определённой формы, будь то треугольники (длина цикла L = 3), квадраты (регулярная сетка c L = 4) или в виде сот (L = 6). Для первого случая (L = 3) достаточно вычислять коэффициент кластеризации C, который показывает количество треугольников в сети. Для более сложных циклов такой метод окажется бесполезным, поскольку коэффициент кластеризации будет давать нулевое значение для любого цикла с L ≠ 3. Поэтому быловвёдено понятие коэффициента «сетчатости» (meshedness coefficient), который позволяет оценить структуру сети с циклами произвольных длин.

Коэффициент сетчатости определяется по формуле M=F/F_max, где F – количество граней (без внешней грани) планарного графа с количеством вершин N и количеством рёбер K, которое может быть выражено через формулу Эйлера F=K-N+1. F_max – это максимально возможное число граней в связном планарном графе с тем же количеством вершин N и, соответственно, количеством рёбер K_max=3N-6. (так как связный граф – это граф, в котором все вершины связаны). Таким образом, F_max=2N-5 и значение коэффициента сетчатости может принимать значение от нуля (древовидная структура) до единицы (связный граф). Значит, при увеличении коэффициента сетчатости, сложность структуры сети увеличивается.

Для количественного описания дорожных сетей каждого города подсчитаем число циклов длины три, четыре и пять, обозначив их соответственно С₃, С₄  и С₅ и ,  ,  для соответствующего GT графа.
Эти показатели рассчитываются на основе матрицы смежности сети. Например, для числа циклов равных трем, соответствующая формула имеет вид     Результаты расчетов даны в таблице 1 [8].

Таблица 1.  Локальны свойства дорожных сетей некоторых городов мира.

	Город	M
1	Ахмедабад	0.262	0.023	0.042	0.020
2	Барселона	0.275	0.019	0.101	0.019
3	Болонья	0.214	0.015	0.048	0.013
4	Бразилиа	0.147	0.029	0.027	0.012
5	Каир	0.253	0.020	0.043	0.019
6	Ирвин 1	0.085	0.035	0.022	0.005
7	Ирвин 2	0.014	0.007	0.004	0.001
8	Лос-Анджелес	0.211	0.002	0.075	0.011
9	Лондон	0.249	0.011	0.060	0.020
10	Нью-Дели	0.154	0.011	0.020	0.011
11	Нью-Йорк	0.348	0.024	0.136	0.028
12	Париж	0.241	0.028	0.063	0.016
13	Ричмонд	0.279	0.034	0.068	0.022
14	Саванна	0.322	0.002	0.111	0.026
15	Сеул	0.253	0.021	0.051	0.021
16	Сан-Франциско	0.309	0.003	0.148	0.003
17	Венеция	0.152	0.016	0.030	0.010
18	Вена	0.242	0.007	0.063	0.018
19	Вашингтон	0.293	0.026	0.132	0.022
20	Уолнат-Крик	0.084	0.000	0.011	0.003

Получается, что дорожные сети Нью Йорка, Сан Франциско и Саванна имеют наиболее сложную картину – их коэффициент сетчатости  М превышает 0.3. Города Ирвин и Уолнат Крик  имеют наиболее простую древовидную структуру и их коэффициент М меньше 0.1. В семнадцати городах из двадцати    >   и только в Бразилиа, Ирвине1 и Ирвине2 мы видим  превалирование  треугольников (циклов длины три) над квадратами. В Лос Анжелесе, Саванне и Вене   > .

Глобальные свойства дорожных сетей городов

Для оценки глобальных структурных свойств дорожных сетей городов используют следующее понятие глобальной эффективности

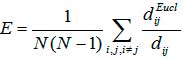
где

d_ij и  есть соответственно наименьшая длина пути  и евклидово расстояние  на плоскости между узлами  и .

Расчеты  глобальной эффективности  дорожных сетей городов и их сравнение  с глобальной эффективности для сетей MST и GT этих же городов показывают, что  только в  Irvin 2 E < E^MST (соответственно,  0. 374 и 0.533), что объясняется тем, что только  для этого города  дорожная сеть не является связной [8].

 Закономерности эволюции дорожных сетей городов

 Многочисленные исследования указывают, что дорожные сети являются важнейшим фактором эволюции городов [4]. Emanuele Strano at al.  [9] исследовали количественные закономерности эволюции дорожной сети Милана  и территории известной как Гроана (Groane ) на севере Милана, площадью 125 квадратных километров, за последние почти 200 лет с точки зрения теории сложных сетей.

В процессе урбанизации этой территории можно выделить четыре этапа:

1. Доиндустриальный период (1800-1918), полностью связанный с сельскохозяйственной экономикой и практическим отсутствием транспортной инфраструктуры.
2. Ранняя фаза урбанизации (1918-1945). Появление железной дороги, небольших центров промышленного производства, постепенное распространение небольших  сельских поселений вокруг исторических центров.
3. Индустриальная фаза (1945-1990). Развитие машиностроительного и текстильного производства, рост населения региона, появление скоростных магистралей.
4. Постиндустриальная фаза (1990-2012). Спад темпов промышленного развития, возникновение центра урбанизации, рост мобильности населения благодаря появлению скоростных поездов.

Количественный анализ эволюции дорожных сетей этой территории соответствовавших 1833,1914,1933,1955,1980,1994 и 2007 годам выявил следующие закономерности. Суммарное число узлов (перекрестков) выросло с 255 в 1833 году до более 5000 в 2007 году. При этом скорость роста числа узлов была низкой в период 1833-1933 годы, высокой в период 1933-1980 годы и снова низкой с 1980 по 2007 годы. Число людей, живших на этой территории, оказалось прямо пропорционально числу узлов, что указывает на равномерное расселение жителей по всей территории и отсутствие единого центра. Кроме того, число связей (дорог) в сети также росло линейно с ростом числа , а суммарная длина дорог L_tot росла по закону L_tot ∝ N^γ , где γ ≈ 0.54.  Если посмотреть на изменение величины

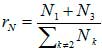, где N_k обозначает число узлов степени k в сети,

характеризующей относительное распространение тупиков (N₁) и Т-образных перекрестков (N₃) в дорожной сети, так что малая величина  указывает на доминирование перекрестков с k = 4, то есть, появление  областей с решетчатой структурой дорог.

Анализ показывает, что величина  последовательно уменьшалась с    в 1833 году до  в 2007 году.  Недавние исследования показали, что распространение Т-образных перекрестков типично для «органических», самоорганизующихся городских дорожных сетей, таких как в Венеции или в Каире, в то время как решетчатая структура свойственна городам, дорожные сети которых планировались изначально, как это было, например, в Нью-Йорке и в Барселоне.

Однако это не означает, что эволюции дорожной сети Гроаны свойственны закономерности самоорганизации в начале и крупномасштабного планирования в конце рассматриваемого периода. Авторы исследования рассматривают эту эволюцию  как процесс постепенного локального территориального упорядочения как результат экономической активности.

Дорожную сеть города можно представить как планарный граф,  состоящий из  ячеек, окруженных участками дорог. Закон распределения площадей этих ячеек, как показали исследования дорожной сети Гроаны (а ранее и Дрездена в Германии), подчиняется степенному закону P (A) ∝ A^-τ , где A- площадь ячеек, τ ≈ 1.9, причем величина этого показателя для Гроаны росла от τ ≈ 1.2 в 1833 году до τ ≈ 1.9 в настоящее время. Поскольку большим значениям τ соответствует более гомогенное (однородное) распределение площадей ячеек, обнаруженный рост величины  τ при эволюции дорожной сети означает наличие процесса гомогенизации в этой эволюции. Анализ изменения  формы этих ячеек выявил четкую тенденцию эволюции от треугольников к прямоугольникам и квадратам. 

Основные закономерности процесса урбанизации

Дорожные сети городов растут путем появления новых дорог и перекрестков. Статистический анализ длины новых дорог выявил четкую тенденцию ее уменьшения за рассматриваемый временной интервал 1833 по 2007 год. Например, средняя длина 90% всех новых дорог построенных за 1833-1933 годы уменьшилась с 625 метров до 325 метров, а в период с 1994 по 2007 год с 325 метров по 225 метров, хотя в интервале 1955-1980 годы наблюдался небольшой рост средней длины дорог.

Рассмотрим понятие важности улиц, уделив основное внимание их загруженности (betweenness centrality). Загруженность BC дорог данной дорожной сети определяется  следующим образом:

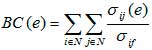, где σ_ij — число кратчайших путей из узла i в узел j, а σ_ij (e) — число кратчайших путей из узла i в узел j, проходящих через дорогу e. По существу, BC(e) показывает сколько раз связь  используется при соединении кратчайшим путем любую пару узлов сети и, таким образом, является мерой вклада данной связи в организацию потоков в сети.

Для того, чтобы оценить вклад новой связи в общее распределение загруженности в сети в любой момент времени, вычислим сначала среднюю загруженность всех связей сети в момент времени t G_t:

Далее, для каждой вновь добавленной связи e^* ∈ ΔE_t во временном интервале [t-1,t] мы рассмотрим новую сеть, получаемую путем удаления  связи e^* из G_t и мы обозначим эту сеть как G_t \{e^*}. Снова вычислим среднее значение загруженности по связям на этот раз для сети G_t \{e^*}. Наконец, вклад δ_b (e^*) связи e^* в загруженность сети в момент t вычисляется следующим образом

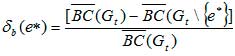
Таким образом, вклад новой дороги (улицы) представляет собой относительное изменение загруженности сети связанное с удалением связи (дороги) e^*. Развитие  территории имеет две сопряженные тенденции: уплотнение и  освоение. В первом процессе (уплотнении) новые дороги связывают уже существующие дороги. При освоении новые дороги заканчиваются тупиками и имеет место урбанизация  сельской территории. Исследование показало, что процесс освоения постепенно исчерпывается и в конечном итоге исчезает, в то время как уплотнение непрерывно продолжается В работе [10]  были предложены другие понятия важности дорог и улиц городов, отражающие меру близости  к другим местам города, а также их доступность из других районов.

Была изучена также связь между возрастом улиц и их загруженностью. Наиболее загруженные улицы, как правило, оказались наиболее древними. В частности, улицы и дороги, существовавшие до 1833 года, оказались намного более загруженными, чем появившиеся позднее. Было замечено также, что исторические районы города  в основном совпадают с наиболее загруженными улицами 2007 года.  Эти же районы во многих случаях оказываются центрами деловой  и торговой активности города [12 ] а также местами, наиболее привлекательными для туристов. Полученные  результаты выявляют основу, «становой хребет» дорожной структуры города, формирующейся еще в его доидустриальный период, но являющийся зародышем будущего процесса урбанизации[9]. 

Заключение

Изучение городской морфологии  и ее развития  показывает, что дороги и улицы существуют гораздо дольше других элементов города, например, зданий и  сооружений и потому понимание  их структурных и динамических свойств имеет чрезвычайно важное значение для выработки общих принципов градостроительной политики. Методы теории сложных сетей, используемые в последнее время в такого рода исследованиях  служат важным дополнительным инструментарием  как при проектировании новых городских территорий, так и обновлении и модернизации старых.

Литература

1. Portugali J. Complexity, Cognition and City. Springer, Berlin, 2011
2. Complexity Theories of Cities Have Come of Age. Editors: Juval Portugali, Han Meger, Egbert Stolk, Ekim TanSpringer, Berlin, Heidelberg, 2012
3. Batty M.& Longley O.A. Fractal Cities: A Geometry, Form and Function (Academic Press, San Diego CA, 1994
4. Southworth M. &Ben-Joseph E. Streets and Shaping of Towns and Cities. (Island Press, Washington DC. USA, 2003)
5. Евин И.А. Введение с теорию сложных сетей. //Компьютерные исследования и моделирование. 2010, Том 2, N2, с. 121-141
6. Caldarelli G. Scale-Free Networks. Complex Webs in Nature and Technology. –Cambridge University Press, 2007. 309 p.
7. Newman M.E. J. The Physics of Networks. // Physical Today. November,33-38, 2008
8. Cardillo A., Scellato S., Latora V., and Porta S. Structural properties of planar graphs of urban street patterns. Physical Review E. 73, 0066107 (2006)
9. Strano E., Nicosia V. , and Barthelemy M. Elementary processes governing evolution of road networks. Scientific Reports. 2:296. DOI: 10.1-38/step00296
10. Crucitti P., Latora V., Porta S. Centrality of Urban Streets. Chaos.16, 015113 (2006)
11. Scellato S.,Cardillo A., Latora V., and Porta S. The Backbone of a City. Eur.Phys.J.B 50, 221-225 (2006)
12. Porta S., Latora V., Wang F., Rueda S., Strano E., Scellato S., Cardillo A., Belli E., Cardenas F.,Cormenzana B, and Latora L. Street Centrality and the Location of Economic Activities in Barcelona. Urban Studies. 1-18, 2011.

Сведения об авторах
Евин Игорь Алексеевич, доктор философских наук, ИМАШ РАН, МФТИ
Букашев Ален Аманжолович, студент МФТИ
Марченко Денис Константинович, студент МФТИ