Введение

В последние годы методы изучения сложных систем путем представления их в виде сетевых структур показал   свою высокую эффективность. Одним из важных направлений таких исследований стало моделирование общественного транспорта мегаполисов и, в частности,  систем подземного транспорта — метрополитенов [1, 2]

Строительство метро стало универсальным, хотя  и далеко не достаточным   решением одной из наиболее острых проблем любого мегаполиса – транспортной проблемы. Такое строительство – весьма дорогостоящее  мероприятие и для оценки долгосрочных вложений в этой области,  желательно иметь достаточно общую модель его развития и эволюции,  а также знание и понимание основных  количественных закономерностей  развития подземного транспорта.

Впервые модель   метрополитена как сложной сетевой структуры предложена  в работах канадского ученого С. Деррибля ( Sybil Derrible) [3,4]. В этих работах изучены сети  метро 33 городов мира. При этом  сравниваются как   локальные свойства и характеристики, так и свойства и характеристики всей сети метро в целом. В работе [5],  на примере  шанхайского метро, рассматривается функционирование  сети  метро при авариях и  целенаправленных террористических актах.

Проблемы изучения эволюции метро как сложной сети

В работе [6] впервые были исследованы некоторые количественные закономерности (рост числа станций, рост числа ветвей и т.п.) эволюции 14 наиболее крупных метрополитенов мира. В статье [2]  показано, что процесс эволюции московского метро можно описать на основе известной модели эволюции безмасштабных сетей Барабаши-Альберт.  При этом сама сеть московского метро как безмасштабная структура сформировалась в 1990 годах и с этого времени, несмотря на продолжающийся рост числа станций, остается безмасштабной сетью. В данной работе рассматривается  изменение загруженности станций московского метро на всем протяжении его эволюции.

Понятие  загруженности B(i) (betweenness centrality) i-того узла определяется кратчайшими путями между узлами сети, которые проходят через  i – узел:

Здесь σ_st(i)– число кратчайших путей из s -узла  в  t –узел, проходящих через  i-узел, а σ_st – общее число кратчайших путей между парами узлов с номерами  s  и  t, которые также имеют соединение через i – узел. Суммирование идет по всем парам узлов, которые имеют соединение через i – узел.   Узлы с высоким значением оценки B  являются наиболее загруженными.

Прежде чем перейти к изучению закономерностей изменения загруженности станций в процессе эволюции московского метрополитена, рассмотрим зависимость числа станций от загруженности  (Рисунок 1)

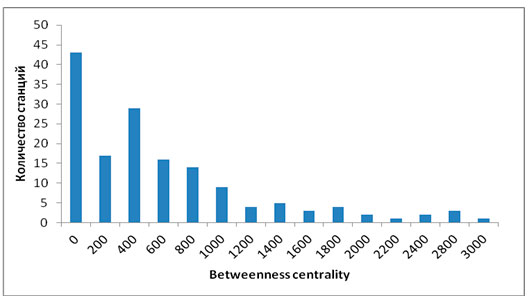
Рисунок 1. График зависимости числа станций московского метрополитена от значения  их загруженности (betweenness centrality)

Расчеты показывают, что эта зависимость является степенной  N ∝ B^-2для любого момента времени функционирования метрополитена как безмасштабной сетевой структуры, что согласуется  с работой [7], в которой показано, что такой закон зависимости является универсальным для  безмасштабных сетей.

На Рисунке 2, на примере станции «Белорусская», представлен типичный характер изменения загруженности станций кольцевой линии московского метро в процессе его эволюции.

Рисунок 2. График изменения загруженности (betweenness centrality)  для кольцевой станции «Белорусская» в процессе развития московского метрополитена

На рисунке 3 представлен аналогичный график для кольцевой станции «Киевская»

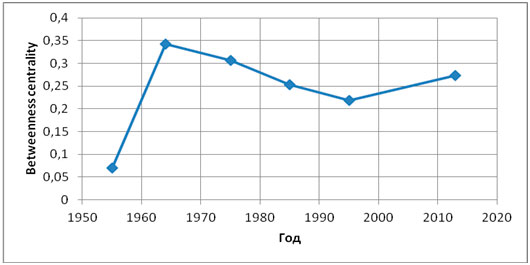 Рисунок 3. График изменения загруженности для кольцевой станции «Киевская»

Рост загруженности в период 1950-1960 годов объясняется вводом в эксплуатацию сразу двух параллельных радиальных веток ведущих к этой станции.  С этого момента сеть московского метрополитена допускает представление   в форме мультиграфа.

На рисунке 4 дан общий график изменения загруженности всех станций кольцевой линии

 Рисунок 4. График изменения загруженности всех станций кольцевой линии московского метрополитена

Рисунок 5 представляет график изменения загруженности  одной из станций, находящейся в центре Москвы

Рисунок 5. Изменение загруженности станции «Охотный ряд/Театральная/Площадь Революции»

В результате выполненного исследования возник  вопрос, является ли  обнаруженное  свойство снижения загруженности станций метро по мере развития города Москвы общим свойством эволюции безмасштабных сетей, или это лишь специфическое свойство развития московского метро. Мы планируем провести специальное исследование, чтобы ответить на этот вопрос.

Перспективы дальнейших исследований

Метрополитен представляет собой наиболее важную составляющую общественного транспорта современного мегаполиса. Автобусный, троллейбусный и трамвайный транспорт также можно моделировать на основе теории сложных сетей [1].  Для моделирования их совместного функционирования в последние годы развивается математический аппарат теории многослойных сетей [8].   Аппарат этой теории позволяет  исследовать проблемы оптимального функционирования всех видов общественного транспорта мегаполиса.

Представляет интерес вопрос включения в многослойную сеть общественного транспорта модели улично-дорожной сети города. Соответствующая многослойная сетевая структура позволяет изучать качественно новые вопросы навигации в городе. Например, в работе [9] показано, что наиболее труднодоступные места города часто являются местами повышенной криминальной опасности, в них  могут скапливаться незаконные мигранты, формироваться  этническая преступность и т.д. Теория многослойных сетей позволяет отслеживать формирование в процессе эволюции города и его транспортной инфраструктуры таких труднодоступных мест.
Все численные расчеты в данной работе были выполнены с использованием пакета программ Gephi.

Литература

1. Евин И.А., Соловьев А.А., Хабибуллин Т.Ф. Модели общественного транспорта Москвы на основе теории сложных сетей // Информатизация и связь. – 2013, №6
2. Евин И.А., Соловьев А.А.,Чернобровкин Д.А. Московское метро как безмасштабная сеть. // Информатизация и связь. – 2013. – №6
3. S.Derrible, C. Kennedy. 2010, The complexity and robustness of metro networks.//Physica. – 2010. – A 389. 678-3691
4.  S.Derrible.The properties and effects of metro network designs. Ph.D. Thesis. Toronto. 2010.
5. Jianhua Zhang, XiaomingXu, Liu Hong, ShuliangWang, Qi Fei.. Networked analysis of the Shanghai subway network in China. // Physica. – 2011. – P 390.    562–457.
6. Roth C., Kang S., Batty M., Barthelemy M. A long-time limit for world subway network. Journal of the Royal Society Interface. – 2012, doi: 10.1098/rsif:2012.0259
7. Goh, K-I., Kahng, B., Kim. D. (2001). Universal behavior of load distribution in scale-free networks. Physical Review Letters, 87, 278701
8. Manlio De Domenico, Albert Solé-Ribalta, Emanuele Cozzo, Mikko Kivelä,  Yamir Moreno, Mason A. Porter, Segio Gómez and Alex Arenas, Mathematical Formulation of Multilayer Networks.  Physical Review X3, 041022 (2013).
9. Philippe Blanchard and Dimitri Volchenkov. Urban Landscape is an Important Factor in Rising Inequality, Spacial Segregation, and Social Isolation.  arXiv: 1312.5057v1. 18 Dec 2013.