Чернавский Дмитрий Сергеевич — профессор ФИАН им. Лебедева

Ранее многие полагали, что молекулярный хаос — удобная форма описания, когда мы не знаем или не можем вычислить истинных траекторий. При этом неявно предполагалось, что вот ужо поднатужимся и сможем предсказать. Теперь мы убеждены, что поведение неустойчивой траектории никто никогда не сможет предсказать — это истинное незнание. Данное утверждение, кажущееся негативным, не менее ценно для науки, чем многие позивитивные

Метод (или математический аппарат), который используется в синергетике, — это теория динамических систем. Математический метод синергетики, то есть теория динамических систем, основан на дифференциальных уравнениях вида

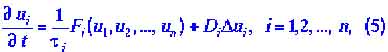где - динамические переменные, например концентрация реагирующих веществ; — функции (в общем случае нелинейные), описывающие их (в смысле динамических переменных) взаимодействие в данной точке пространства; — характерные времена изменения переменных ;
Член описывает распространение динамических переменных в пространстве , в частности их диффузию ( — коэффициенты диффузии).

Уравнения (5) называют также уравнениями реакции с диффузией, поскольку они, в частности, описывают изменения концентрации веществ во времени и пространстве с учетом их диффузии и химических реакций. Принимают, что процессы, описываемые уравнениями (5), протекают в ограниченном пространстве — либо одномерном (реакции в трубке длиной L), либо двухмерном (реакции в пленке шириной порядка L), либо в трехмерном (реакции в сосуде, размеры которого порядка L).

В частном случае, когда все динамические переменные распределены в пространстве равномерно, мы имеем систему обыкновенных дифференциальных уравнений:

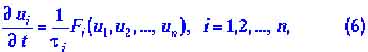Последнее имеет место, если «длины диффузии» превышают пространственные размеры L системы. Уравнения (6), именуемые также точечными, хотя и проще уравнгений (5), тем не менее описывают многие неожиданные и интерсные явления.

Уравнения (5) и/или (6) являются динамическими, т.е. их решения, вообще говоря, однозначно определяются начальными и граничными условиями и, разумеется, свойствами и параметрами самих уравнений. Казалось бы, в такой ситуации ничего неожиданного быть не должно. Тем не менее характерные для синергетики неожиданности здесь возникают в случае, когда решения динамических уравнений теряют устойчивость. Обсудим это важное свойство.

Интуитивное представление об устойчивости (или неустойчивости) есть у каждого. Неустойчиво, например, состояние карандаша, поставленного на острие; неустойчиво движение шарика по гребню. В то же время движение его по ложбине устойчиво. Более точное представление дает анализ уравнений движения (и/или стационарных состояний). Этот анализ основан на исследовании поведения малых отклонений от соответствующего решения. Продемонстрируем это на примере стационарных состояний точечной системы. Стационарными являются состояния, соответствующие таким значениям переменных , при которых все функции равны нулю. При этом значения не меняются со временем, поскольку все производные также равны нулю. Однако малые отклонения от стационарных значений меняются со временем, и их изменение можно описать системой линейных дифференциальных уравнений

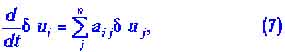где

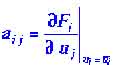Решения имеют вид:

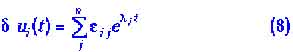Здесь — коэффициенты, пропорциональные начальным отклонениям, ; они малы в меру малости последних.

Величины — числа, которые являются решениями алгебраического уравнения:

где		-символ Кронекера

Величины называются также числами Ляпунова и играют главную роль в анализе устойчивости.Если все числа Ляпунова отрицательны, то состояние устойчиво. Действительно, в этом случае все отклонения со временем уменьшаются, т.е. система стремится обратно к стационарному состоянию, даже если ее немного отклонить от него. Если хотя бы одно из чисел Ляпунова положительно, то состояние неустойчиво. Действительно, тогда отклонения возрастают со временем, причем достаточно быстро. Так в упомянутом примере — карандаш на острие — среди чисел Ляпунова имеются положительные по порядку величины равные . Это значит, что за время порядка 10 с начальные отклонения возрастут в раз. Это колоссальная величина; она означает, что карандаш простоит на острие 10 секунд, только если начальные отклонения были бы меньшесм. Это абсурдно малая величина; фиксировать начальные условия с такой точностью, разумеется, невозможно.
В общем случае числа Ляпунова могут быть комплексными. Устойчивость определяется тогда знаком реальной части. Если среди чисел Ляпунова имеются равные нулю или чисто мнимые, то стационарное состояние называется нейтральным; при отклонении от него не появляются ни возвращающие, ни отклоняющие силы.
Анализ неустойчивых движений основан на том же принципе: определяется временная зависимость малых отклонений от заданной траектории. Используются линейные по отклонениям уравнения (высшими степенями пренебрегают), решения которых имеют вид:

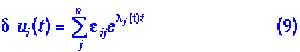Числа Ляпунова при этом уже не постоянны, а зависят от времени. Траектория является неустойчивой, если среди чисел имеются такие, вещественные части которых положительны при .

Подчеркнем важное свойство: числа Ляпунова являются характеристическими (или собственными) числами системы; они не зависят от начальных условий. Таким образом, устойчивость (или неустойчивость) — внутреннее свойство исследуемой системы, а не результат внешнего воздействия. Особенность его в том, что проявляется оно только при наличии малых внешних воздействий.
Эта особенность привела к важным методологическим последствиям. Сейчас приходится пересматривать и подвергать ревизии некоторые, казалось бы, установившиеся в физике понятия.

Обсудим два примера.

Рассмотрим понятие абсолютно изолированной системы. Сейчас ясно, что его можно (и то не всегда) ввести лишь как предел неизолированной системы при стремлении к нулю величины внешнего воздействия. Для устойчивых систем такой предел существует и, следовательно, понятие остается в силе. В неустойчивых системах такой предел, вообще говоря, не существует. Действительно, предел величины , где , при и зависит от порядка стремления аргументов к своим пределам. Формально величину (которая отражает меру внешних воздействий) и время можно считать независимыми. Однако как мы уже убедились на конкретном примере, уже при сравнительно небольших временах экспонециальный фактор возрастает столь сильно, что компенсировать его уменьшением — задача абсурдная. Суть дела в том, что экспонециальная зависимость ( ) очень сильна, конкурировать с ней практически невозможно. Поэтому для неустойчивых систем понятие «абсолютно изолированная система» теряет смысл; можно лишь говорить об относительно изолированной системе.

Требует ревизии и понятие «причины». Обычно под причиной понимают начальные условия (или импульсные внешние воздействия), которые в соотвествии с динамикой системы приводят к определенному результату — следствию. На этом языке слова «вскрыть причинно-следственные связи» означает «понять динамику промежуточных процессов». При этом негласно предполагают, что причины и следствия соизмеримы. Для устойчивых (или нейтральных) процессов это всегда имеет место. В неустойчивых процессах ситуация иная: очень малая причина приводит к следствию, которое по массштабам с причиной несоизмеримо. Обычно в таких случаях говорят, что причиной явилась неустойчивость, а не малое начальное воздействие. При этом, однако, происходит весьма существенный сдвиг понятий: в качестве причины фигурирует внутреннее свойство системы, а не внешнее воздействие.

Поясним сказанное на житейском примере. Рассмотрим два случая. В первом хрустальная ваза стоит на середине стола (состояние устойчиво). Прошел некто и неловким движением толкнул вазу со стола — она разбилась. В чем причинв столь печального события, или, другими словами, кто виноват? Понятно, что виноват «некто», а причина — его неловкие движения.

Рассмотрим другой случай: ваза стоит на краю стола, так что чуть-чуть не падает (состояние, близкое к неустойчивому). Пролетела муха — ваза разбилась. В этом случае муху не обвиняют, а говорят, что причина событий в неустойчивом положении вазы. Виноват тот, кто ее поставил (так, чтобы никто не был виноват, в жизни обычно не бывает).

Забегая несколько вперед, отметим, что в основе утверждения «событие произошло случайно» (т.е. без видимой причины) также лежит неустойчивость динамических систем. (Чернавский. с. 12-14)

Динамический хаос. (Д.С.Чернавский)

Один из самых интересных и важных разделов синергетики — так называемый динамический хаос. Как в рамках чисто динамической системы возникает хаотический режим с непредсказуемым поведением?
Вопрос это возник сравнительно давно, и история его не лишена драматизма. Людвиг Больцман поставил себе целью «вывести» законы термодинамики, в частности закон возрастания энтропии, из законов классической мехакники. В качестве модели идеального газа он рассмотрел систему из многих шаров (число шаров N>>1), которые двигаются и упруго сталкиваются друг с другом. Эта модель получила название «задача о бильярде». С точки зрения синергетики эта модель — динамическая система, содержащая 6N переменных (координаты и скорости всех шаров в трехмерном пространстве). Соответственно фазовое пространство системы многомерно, т.е. содержит 6N измерений. Полная энергия системы сохраняется (как и полагается в классической механике), т.е. система консервативна. Это значит, что соударения абсолютно упругие и «трение» на участках между соударениями отсутствует, поскольку молекулы (т.е. шары) летят в вакууме.

Поставленную задачу Больцман решил, т.е. вывел так называемую H-теорему, продемонстрировал необратимое возрастание энтропии и выяснил микроскопический смысл самого понятия энтропии. Именно он показал, что энтропия пропорциональна логарифму вероятности застать систему в определенном состоянии (в котором положения и скорости всех шаров фиксированы). В процессе вычислений Больцман использовал гипотезу о том, что изображающая точка, двигаясь по фазовой траектории, равномерно заполняет все доступное фазовое простраство.

Гипотеза получила название молекулярного хаоса, она казалась вполне естественной, хотя в то время и не была обоснована. Результаты Больцмана вошли в науку как замечательное достижение человеческого разума. Тем не менее триумф Больцмана был омрачен. Его коллега и друг математик Цермело сказал, что Больцман в расчетах где-то допустил ошибку. Действительно, исходная система уравнений, которую использовал Больцман, консервативна и обратима во времени (как и любая механическая система без трения), в то время как конечный результат — возрастание энтропии — явно необратим. Следовательно, где-то в расчетах нарушена симметрия исходных положений (в данном случае симметрия относительно обращения времени); нарушать симметрию нельзя (во всяком случае без веских причин). Больцман не смог ответить Цермело и застрелился.

Следующим был замечательный физик Эренфест. Он взялся за решение задачи и сформулировал проблему максимально четко, но решить ее не смог и застрелился. Ответ был дан (точнее, сформулирована основная идея ответа) только в 1948 году молодым физиком Н.С.Крыловым. Главная идея сводилась к следующему: симметрия в динамических системах может нарушаться и молекулярный хаос может возникать, если динамические решения неустойчивы. Сформулировав эту идею Н.С.Крылов скончался.

Последовательная математическая теория была развита в работах школы Колмогорова Д.В.Амосовым и Я.Г.Синаем. Было показано, что в задаче о бильярде любая траектория системы неустойчива, т.е. фазовое пространство сплошь состоит из сепаратрис *), а устойчивых состояний вообще нет.
—————
*) Сепартриса — это линия разделяющая области притяжения **) в фазовой плоскости.
**) Области притяжения в фазовой плоскости — это области, имеющие устойчивое состояние, к которому стремятся траектории движения изображающей точки в фазовой плоскости, сопоставленной данной динамической сиcтеме.
——————

Продемонстрируем этот эффект.
Соударение двух шаров радиуса r можно свести к задаче об отображении точки от выпуклой поверхности радиуса 2r. Пусть до соударения траектории были отклонены друг от друга на малый угол . После соударения угол становится существенно больше. Его легко вычислить, используя закон упругого отражения и элементарную геометрию:

где	длинна пробега между соударениями	-угол удара

Отсюда видно, что при каждом соударении угол отклонения возрастает и после n-го удара будет равен

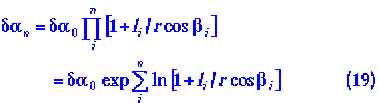Число соударений n растет со временем , где — частота соударений. Поэтому формулу (9) можно представить в в виде:

здесь

черта сверху означает усреднение по данной траектории.
Величина является числом Ляпунова; она положительна, и следовательно, отражение от выпуклой поверхности неустойчиво.

Сделаем ряд замечаний.

Полагая, что в формуле (21) , видим, что . Это значит, что при дальнодействующих силах глобальная неустойчивость отсутствует, даже если число взаимодействующих объектов в системе велико. Этот вывод очень важен; действительно, число объектов, например в Солнечной системе достаточно велико: это планеты, их спутники и т.д. Однако благодаря дальнодействию эти объекты не сталкиваются и движутся по вполне опредленным траекториям. Глобальной неустойчивости и хаоса в этой системе нет, что и позволяет нам жить относительно спокойно.

Таким образом, для возникновения молекулярного хаоса необходимым и достаточным условием является глобальная неустойчивость. Большое число частиц не является ни необходимым, ни достаточным условием; это следует подчеркнуть, поскольку до недавнего времени (да и сейчас) в солидных книгах часто утверждалось обратное. Сейчас Больцман мог бы ответить Цермело вполне обоснованно и указать не только «причину» молекулярного хаоса, но и очертить область применимости этой гипотезы, в частности привести примеры, в которых она не реализуется.

Теория динамического хаоса имеет также и методологическое значение. Ранее многие полагали, что молекулярный хаос — удобная форма описания, когда мы не знаем или не можем вычислить истинных траекторий. При этом неявно предполагалось, что вот ужо поднатужимся и сможем предсказать. Теперь мы убеждены, что поведение неустойчивой траектории никто никогда не сможет предсказать — это истинное незнание. Данное утверждение, кажущееся негативным, не менее ценно для науки, чем многие позивитивные. (Чернавский. с.17-19)

Чернавский. Д.С.Чернавский. Синергетика и информация. — М.: Знание, 1990.- 48 с. — ( Новое в жизни, науке, технике. Сер. «Математика,кибернетика»; N5)