In late 1995 Mike Simmons, then-SFI vice president, introduced me to Jim Brown. At that time I was overseeing the high energy physics program at Los Alamos National Laboratory while Brown, who had recently moved to the University of New Mexico’s biology department, was developing an ecology program at SFI. Serendipitously we had both been thinking about a longstanding problem in biology, namely the origin of so-called “quarter-power allometric scaling laws.” I will elaborate on what this means later but, roughly speaking, it refers to the surprising observation that across the entire spectrum of life, almost all physiological variables and life-history events scale with size in a remarkably simple, systematic, and predictable fashion.
Sandwiched between quarks, Higgs, strings, and dark matter, I had been struggling with developing a physics-inspired network theory for the origin of these scaling laws, while Brown and his then-student, Brian Enquist (now at the University of Arizona), had been speculating that nutrient transportation through the bloodstream was a key ingredient.

Simmon’s intuition that we might have something to say to one another changed our lives and marked the beginning of what became known as the “scaling program” at SFI. The implications of scaling phenomena later expanded beyond biology, ecology, and biomedicine to embrace human socioeconomic systems such as cities and companies – even extending to the challenge of global sustainability. Thus began a beautiful relationship with Brown, Enquist, and SFI and, by extension, with the ensuing cadre of wonderful postdocs, students, and faculty who have since worked on the Institute’s scaling and cities programs.
Our sustained collaboration has been enormously productive, extraordinarily exciting, and tremendously fun. Beginning in 1996, initially with Brown, Enquist, and me, and later with the expanded group, we met every Friday at SFI from 9 a.m. to around 3 p.m. This continued almost uninterrupted until just the last couple of years. At the outset this was a huge commitment as both Brown and I ran large research groups elsewhere.
Once the ice was broken and some of the cultural barriers were crossed, we created a refreshingly open atmosphere where all questions and comments, no matter how elementary, speculative, or seemingly stupid, were encouraged, welcomed, and treated with mutual respect. There were lots of arguments, speculations, and explanations; struggles with big questions and small details; lots of blind alleys; and an occasional aha! moment – all against a backdrop of a whiteboard (and sometimes Institute windows) covered with equations, graphs, and illustrations. Brown and Enquist patiently acted as biology tutors, exposing me to the world of natural selection, evolution, adaptation, fitness, physiology, and anatomy, all of which were embarrassingly foreign to me. For my part, I tried to reduce complicated mathematical equations and technical physics arguments to relatively simple, intuitive calculations and explanations. In other words, we were engaged in a typical transdisciplinary Santa Fe Institute experience!

Recent research at SFI considers the city not only as people and infrastructure, but as a network of interactions in space and time. In this nighttime satellite image, populated areas branch out from the New York City metropolitan area. (NASA)
So what is “scaling”? In its most elemental form, it simply refers to how systems respond when their sizes change. What happens to cities or companies if their sizes are doubled? What happens to buildings, airplanes, economies, or animals if they are halved? Do cities that are twice as large have approximately twice as many roads and produce double the number of patents? Should the profits of a company twice the size of another company double? Does an animal that is half the mass of another animal require half as much food?
Asking such seemingly innocuous questions has had remarkably profound consequences across the spectrum of science, engineering, and technology and has impacted almost every aspect of our lives, even including how we perceive our place in the universe. Over the past 50 years, scaling arguments have led to a deeper understanding of the dynamics of tipping points and phase transitions (how, for example, liquids freeze into solids), chaotic phenomena (the mythical flapping of a butterfly’s wings in Brazil stimulating a hurricane in Florida), the discovery of quarks (the building blocks of matter), the unification of the fundamental forces of nature, and the evolution of the universe after the Big Bang. Three Nobel prizes have involved discoveries related to scaling during the past 30 years.
In a more practical context, scaling plays a critical role in the design of increasingly large human engineered artifacts, such as buildings, bridges, ships, airplanes, and computers, where extrapolating from the small to the large in an efficient, cost-effective fashion is a continuing challenge. (Indeed, simply doubling all dimensions of a bridge in order to traverse a river twice as wide would very likely lead to it collapsing under its own weight.) Even more challenging, and of perhaps greater urgency, is to understand how to scale organizational structures of increasingly large and complex cities, corporations, and governments, where underlying principles are typically not well understood because these – like living systems – are continuously evolving and adapting.

Scaling from small to large in an efficient, cost-effective manner plays a critical role in the design of increasingly large human engineering projects, such as the effort now underway to replace the 16,000-ft. cantilevered Tappan Zee Bridge that spans New York’s Hudson River. (Artists rendition of future bridge design, New York State Thruway Authority)
Our research was originally stimulated by the observation that, despite the extraordinary complexity and diversity of life, many of its most fundamental metrics scale in a remarkably simple and systematic fashion across an immense range, from cells to ecosystems. The best known of these is for metabolic rate (the rate at which energy is needed to sustain an organism), which scales as a so-called power law with an exponent of ¾ over an astonishing 27 orders of magnitude. In English, this means that doubling the size of an organism from, say, 10g to 20g, or from 100kg to 200kg, only requires an increase in metabolic energy (food intake) of about 75%, rather than 100%, as might naively be expected. Remarkably, this systematiceconomy of scale permeates biology. Similar systematic scaling laws hold for almost any measureable physiological trait or life-history event: life spans, growth rates, DNA nucleotide substitution rates, genome lengths, tree heights, and the mass of cerebral grey matter. Of equal importance, the corresponding exponents express a universality, invariably approximating simple multiples of ¼. (This is the origin of the phrase “quarter-power allometric scaling” introduced at the beginning of this article; the term “allometry” was coined in 1936 by Julian Huxley and Georges Tessier to designate scaling in biology, though the ¾ power law for metabolic rate was proposed earlier by Max Kleiber in 1932.)
The predominance of quarter-power scaling across all life forms is particularly surprising because each organism, each sub-system, each cell type, and each genome has evolved in its own particular, ever-changing environmental niche with its own unique circumstances and history. Thus, one would not have expected any systematic behavior to have emerged. Instead, we might expect a huge variance reflecting the historical contingency and randomness implicit in natural selection. The presence of regularity strongly suggests that generic underlying dynamical mechanisms have constrained evolutionary processes, thereby opening a possible window into determining quantifiable emergent laws that capture the essential features and coarse-grained behavior of living systems. Although the problem had attracted the attention of many biologists, including Huxley, Haldane, and D’Arcy Thompson, no general theory had yet been developed when we began to address these questions in 1995.



Networks require an efficient supply of nutrients. Left: leaf vasculature (istockphoto.com). Middle: satellite image of London (NASA). Right: Mouse retina with vaculature in blue (NIH).
We conjectured that the key lies in the generic mathematical properties of networks. Highly complex self-sustaining systems – whether they are cells, organisms, ecosystems, cities, or corporations – require close integration of many constituent units that require an efficient supply of nutrients and the disposal of waste products. We suggested that this servicing – via, for instance, circulatory systems in organisms, or perhaps transport systems in cities – is accomplished through optimized, space-filling, fractal-like branching networks whose dynamical and geometric constraints are independent of specific evolved organismic design.
Eventually these ideas led to a general quantitative, predictive mathematical framework for deriving quarter-power scaling and for understanding many essential features of diverse biological systems and functions, including vasculature, forest communities, tumors, aging and death, sleep, cell size, and evolutionary rates. Because these branching networks determine rates at which energy and resources are delivered to functional terminal units, such as cells, they set the pace of physiological processes and life history events, such as life spans, turnover times, and growth rates. The theory predicted, in agreement with observation, that, from cells and whales to community structures, the pace of life systematically and predictably slows down with increasing size, and that this is accompanied by increasing economies of scale. Much of this body of work became known as the metabolic theory of ecology.
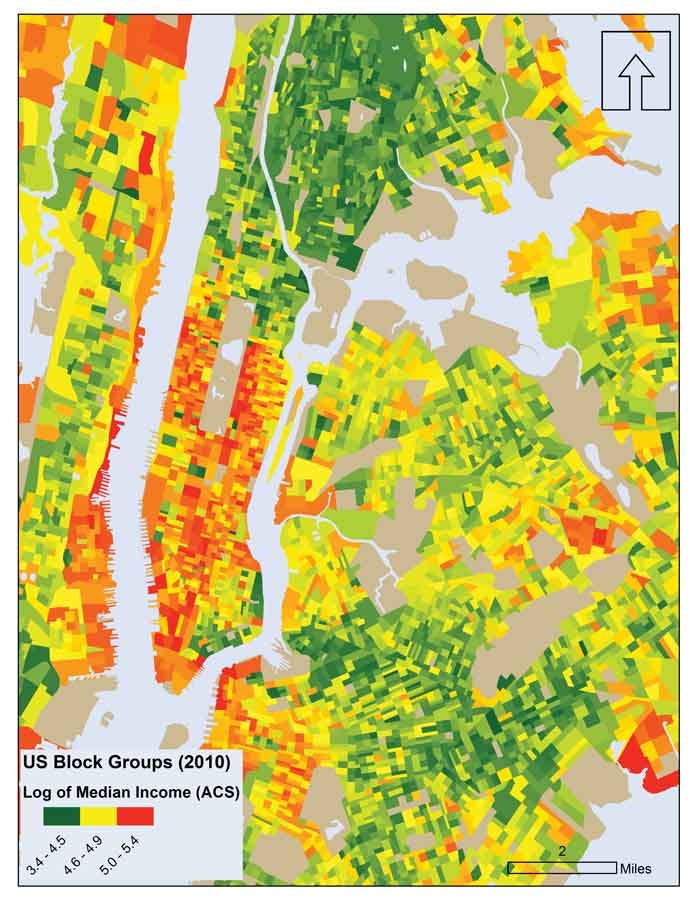
SFI researchers have examined the underlying structures of networks and how they influence city dynamics. Here, a data map of Manhattan and surrounding areas shows average household wealth by borough. Shades of red are the highest-income areas. Shades of green are the lowest-income neighborhoods. (Clio Andris)
The theory’s success naturally led to a possible extension to other networked systems, such as cities and companies, which superficially have much in common with organisms and ecosystems. This new exploration began with informal discussions at SFI around 2002 between David Lane (who had previously run the Institute’s economics program), Sander van der Leeuw (an anthropologist then on sabbatical at SFI, now at Arizona State University), and myself. We soon became joint principal investigators – with Denise Pumain (an urban geographer at the Sorbonne) – of a broad European Union-funded program we called ISCOM (the Information Society as a Complex System). A major component of this effort was to ask whether cities also manifest scaling and, if so, to develop a quantitative and principled theory for understanding the structure and dynamics of urban systems. To address these challenges, a new multidisciplinary SFI-style collaboration was assembled.
With Dirk Helbing (a physicist, now at ETH Zurich) and his student Christian Kuhnert, and later with Luis Bettencourt (a Los Alamos physicist now an SFI Professor), Jose Lobo (an economist, now at ASU), and Debbie Strumsky (UNC-Charlotte), we discovered that cities, like organisms, do indeed exhibit “universal” power law scaling, but with some crucial differences from biological systems.
Infrastructural measures, such as numbers of gas stations and lengths of roads and electrical cables, all scale sublinearly with city population size, manifesting economies of scale with a common exponent around 0.85 (rather than the 0.75 observed in biology). More significantly, however, was the emergence of a new phenomenon not observed in biology, namely,superlinear scaling: socioeconomic quantities involving human interaction, such as wages, patents, AIDS cases, and violent crime all scale with a common exponent around 1.15. Thus, on a per capita basis, human interaction metrics (which encompass innovation and wealth creation) systematically increase with city size while, to the same degree, infrastructural metrics manifest increasing savings. Put slightly differently: with every doubling of city size, whether from 20,000 to 40,000 people or 2M to 4M people, socioeconomic quantities – the good, the bad, and the ugly – increase by approximately 15% per person with a concomitant 15% savings on all city infrastructure-related costs.

The world is urbanizing at an unprecedented pace, requiring new and growing cities, especially in India, China, and parts of the developing world. Mumbai housing construction seen here.
No wonder cities have continued to grow. When we move to a city within an urban system that is twice as large, we become, on average, 15% more wealthy, more productive, more creative…and we do this using a fraction of the infrastructure. The discovery of economies of scale and the resulting fruits of innovation and wealth creation brought a fundamentally new dynamic beyond classic biology to the planet. This surprising universality is observed in urban systems in the United States, China, Japan, Europe, and Latin America and transcends history, geography, and culture. What a remarkable outcome manifested in the emergent behavior resulting from human interaction and social networking!
As in biology, these regularities have led to the beginning of a quantitative theory of cities based on the underlying dynamics and organization of social networks, integrated with the physical networks of urban infrastructure. Fundamentally, cities are facilitators of social interaction. Our collaboration has been exploring the multiple implications and extensions inspired by this conceptual framework. In addition to developing the basic theory, we are exploring, among many other topics, the questions of open-ended growth and the increasing pace of life, the diversity of businesses and employment, the consequences and benefits of the rapid migration into cities we are witnessing today, and the statistics of how cities deviate from scaling regularities and what that implies for particular cities. Our theoretical predictions have been confirmed for urban social interactions across time and space, from the fascinating study led by Luis Bettencourt and Scott Ortman on pre-Columbian Mexican settlement data, to a recent analysis of 21st century cell phone data we conducted in collaboration with colleagues at MIT. In related research led by Bettencourt, the work is being extended to a better understanding of slums, informal communities, and neighborhoods – all of which play an important role in the development of megacities.

Rapid urbanization means cities often grow faster than infrastructures. When they do, informal settlements, such as this slum in Sierra Leone, often arise. Recent SFI research seeks to understand the dynamics of rapid city growth, both to help slum dwellers articulate their needs and help decision makers better manage growth and the human development that (ideally) does goes with it.
Perhaps of even greater relevance is that the long-term sustainability of the planet is inextricably linked to the fate of our cities. We are urbanizing at an exponential rate, with more than half of the world’s population now living in urban centers. The biggest global challenges we are facing from climate change, the environment, availability of energy and resources, social unrest, and financial markets are generated in cities, but cities are also the hubs of innovation, wealth creation, and power. Put slightly differently, cities may well be the problem, but they are also the solution. This strongly suggests that there is a great urgency to develop a more quantitative, predictive, computational framework that can complement the traditional, more qualitative, narrative approaches to understanding cities – a framework that can help inform today’s and tomorrow’s practitioners and policy makers.
