Георгий Малинецкий
gmalin@keldysh.ru

КОНЕЦ ГЛАВЫ

Правильнее будет сказать, что для данной точности (сколь угодно большой, но конечной) можно всегда указать такой промежуток времени, что для него становится невозможным сделать предсказания. И этот промежуток (и в этом вся соль) не так уж велик.
«Фейнмановские лекции по физике»

Эта сказка имеет счастливое начало. В 1963 году Рэй Брэдбери опубликовал фантастический рассказ, в котором сформулировал идею динамического хаоса. В этом рассказе один из организаторов предвыборной кампании после победы своего кандидата отправляется в путешествие по времени. Фирма, организующая такую поездку, предлагает охоту на динозавров, которым в ближайшее время суждено умереть. Чтобы не нарушить сложную ткань причинно-следственных связей и не изменить будущее, следует двигаться по специальным тропам. Однако герой не смог выполнить этого условия и нечаянно раздавил золотистую бабочку. Возвратившись назад, он видит, что изменились состав атмосферы, правила правописания и итог предвыборной кампании. Едва заметное движение повалило маленькие костяшки домино, те повалили костяшки побольше, и, наконец, падение гигантских костяшек привело к катастрофе. Отклонения от исходной траектории, вызванные раздавленной бабочкой, стремительно нарастали (см. рис. 1). Малые причины имели большие следствия. Математики называют это свойство чувствительностью к начальным данным.

В том же 1963 году мысль о принципиальной ограниченности нашей способности предсказывать (или, как сейчас говорят, о существовании горизонта прогноза, или пределов предсказуемости) даже в мире, который идеально описывается классической механикой, была высказана лауреатом Нобелевской премии Ричардом Фейнманом. Для существования горизонта прогноза не нужно, чтобы «Бог играл в кости», добавляя в уравнения, описывающие нашу реальность, какие-то случайные члены. Не надо опускаться на уровень микромира, на котором квантовая механика дает вероятностное описание Вселенной. Объекты, поведение которых мы не можем предсказывать на достаточно большие времена, могут быть очень простыми. Таковы, например, незамысловатые системы маятников с магнитиками, которые сейчас продаются во многих лавках как произведения «динамического искусства» (dynamic art).То, что чувствительность к начальным данным ведет к хаосу, понял — и тоже в 1963 году! — американский метеоролог Эдвард Лоренц. Он задался вопросом: почему стремительное совершенствование компьютеров не привело к воплощению в жизнь мечты метеорологов — достоверному среднесрочному (на 2-3 недели вперед) прогнозу погоды? Эдвард Лоренц предложил простейшую модель, описывающую конвекцию воздуха (она играет важную роль в динамике атмосферы), просчитал ее на компьютере и не побоялся всерьез отнестись к полученному результату. Этот результат — динамический хаос- есть непериодическое движение в детерминированных системах (то есть в таких, где будущее однозначно определяется прошлым), имеющее конечный горизонт прогноза.

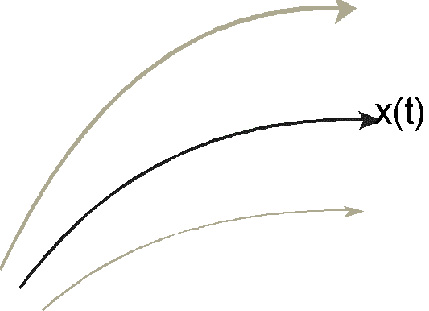Рис. 1. Любая динамическая система определяет траекторию в фазовом пространстве, например, такую, как показана красным цветом. Динамический хаос обусловлен тем, что соседние траектории (показанные зеленым) удаляются от нее. Из-за этого малые причины могут иметь большие следствия.

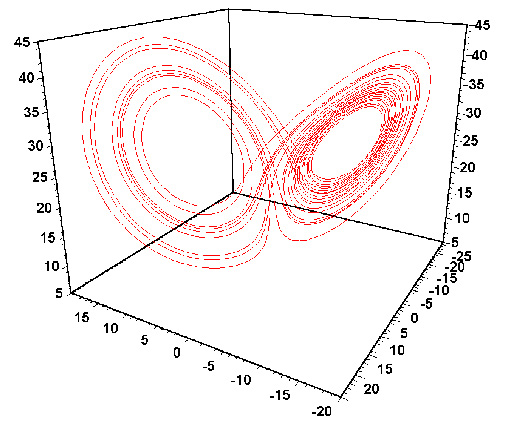Рис. 2 Такая картина, полученная на компьютере, убедила Э. Лоренца, что он открыл новое явление — динамический хаос. Этот клубок траекторий, называемый сейчас аттрактором Лоренца, описывает непериодическое движение. Движение в этом случае не станет периодическим, сколько бы мы ни ждали.

Увиденное Лоренцем показано на рис. 2. С точки зрения математики можно считать, что любая динамическая система, что бы она ни моделировала, описывает движение точки в пространстве, называемом фазовым. Важнейшая характеристика этого пространства — его размерность, или, попросту говоря, количество чисел, которые необходимо задать для определения состояния системы. С математической и компью-терной точек зрения не так уж и важно, что это за числа — количество рысей и зайцев на определенной территории, переменные, описывающие солнечную активность или кардиограмму, или процент избирателей, до сих пор поддерживающих президента. Если считать, что точка, двигаясь в фазовом пространстве, оставляет за собой след, то динамическому хаосу будет соответствовать клубок траекторий. Например такой, как показан на рис. 2. Здесь размерность фазового пространства всего 3. Замечательно, что такие удивительные объекты существуют даже в трехмерном пространстве. Для таких клубков другие классики нелинейной науки Д. Рюэль и Ф. Такенс в 1971 году придумали красивое название — странный аттрактор.

Будучи собраны воедино, отдельные модели, компьютерные эксперименты, наблюдения дали чарующую картину. Среди фрагментов этой мозаики есть пророчество Анри Пуанкаре о том, что в будущем можно будет предсказывать новые физические явления, исходя из общей математической структуры описывающих эти явления уравнений. Компьютерные эксперименты превратили эту мечту в реальность. Другой фрагмент — усилия теоретиков, обосновавших статистическую физику и разбиравшихся, почему и как о движении, о динамике можно говорить на вероятностном языке. Важный элемент мозаики — появившийся в 80-е годы междисциплинарный подход: синергетика, или нелинейная динамика. Динамический хаос стал одним из китов, на котором она стоит.
80-е годы — эпоха безудержного оптимизма и эйфории. Динамический хаос позволил в ряде случаев диагностировать серьезные заболевания по данным об электрической активности с помощью довольно простых компьютерных программ. Экономические прогнозы, опирающиеся на представления о хаосе и странных аттракторах, стали отраслью индустрии. Нельзя не вспомнить о «нелинейных журналах» — «Physica D», «Chaos», «Nonlinearity», «Physical Review E», «Прикладная нелинейная динамика» и прочая, прочая, прочая.
Блестящий успех — открытие сценариев перехода от порядка к хаосу. Независимо от того, какими уравнениями описывается система, в нашем мире есть всего несколько универсальных сценариев. Они не зависят от того, открываем ли мы кран, глядя, как плавный упорядоченный поток превращается в хаотический, турбулентный, или доливаем раствор в пробирку, где идет хаотическая химическая реакция, позволяющая любоваться причудливой игрой цветов. За многообразием обнаружилось внутреннее единство. Казалось, еще немного и — откроются двери в сказку…
Но этого не произошло. Прекрасный принц не примчался к Золушке. Герда не нашла Кая. Рыцарь не победил дракона. На состоявшейся недавно конференции «Хаос-98″ в Саратове было много блестящих докладов. Как и положено в эпоху постмодерна, в них было много деталей, тонкостей, отголосков предыдущих эпох, прожитых нелинейной динамикой. Конечно, все это радует душу профессионалов, но рассказывать о полученных результатах непосвященному становится все труднее. Поэтому серьезные исследователи в кулуарах всерьез обсуждали, как сделать так, чтобы их научное сообщество не превратилось в «секту динамического хаоса», «клуб нелинейных динамиков» или во «фракцию синергетиков».
Эта глава нелинейной динамики закончилась. Надо перевернуть страницу, подумать и начать писать дальше.
ЧТО ЗА НАУКОЙ ПОСТМОДЕРНА?
Игру в бисер тоже не забудут,
но исчезнет она безвозвратно,
и те, кому случится потом
изучать ее историю,
ее возникновение, расцвет
и конец, будут вздыхать
и завидовать нам.
Г. Гессе. «Игра в бисер»
Оказавшись в тупике и разыскивая путь, естественно взглянуть на весь ландшафт сверху. Итак, спросим себя: что в XX веке общество ждало от фундаментальной науки, от игроков в бисер? Какие задачи оно ставило перед исследователями? По-видимому, главных задач было три.
Первое — создание меча и, соответственно, щита. Для этого доказывались теоремы, строились изящные теории, проводились расчеты и ставились опыты. Однако, вероятно, эта сверхзадача в большой степени исчерпана. Гонку вооружений в нашем мире сменила гонка разоружений. Заключаются договоры о сокращении различных видов оружия, о запрещении испытаний и нераспространении многих военных технологий. С вооружения снимаются сверхсовершенные образцы «специальной техники», которые никогда не использовались. Их не заменяют. По оценкам, убийство каждого человека во время операции «Буря в пустыне» обошлось державам коалиции, взявшимся наводить порядок, более чем в миллион долларов. Человечество почувствовало себя не настолько богатым, чтобы позволить себе воевать.
Вторая задача — создание новых товаров. Но и здесь стал виден край. Можно поставить на полку в универсаме десять сортов пива, можно тысячу, а миллион уже нет. Ресурсов не хватит. Цифры таковы. Чтобы развивающиеся страны начали жить по стандартам развитых, им надо увеличить добычу невосполнимых ресурсов в 70-250 раз (по разным видам сырья этот показатель различен), а тогда всего хватит совсем ненадолго. Поэтому все чаще речь идет не о новых товарах и технологиях, а о том, чтобы делать то же самое быстрее и дешевле. А это уже не сверхзадача.
Третья проблема — построение научной картины мира. Тут дела обстоят совсем не благополучно. Античная наука имела дело не только с теоремами и доказательствами, но и со смыслами и ценностями. XX век разделил исследователей на две категории. Одних он превратил в ремесленников, которые могут многое сделать, не очень задумываясь над вопросом, следует ли этим заниматься. Других — в специалистов по общим истинам, не различающих тех частностей, к которым эти истины относятся. Пропасть между двумя культурами — естественнонаучной и гуманитарной, о которой с тревогой говорил сорок лет назад писатель и физик Чарльз Сноу, так и не удалось преодолеть.
Быть может, сбывается мрачное пророчество одного из отцов квантовой механики Е. Вигнера о том, что наука имела начало и будет иметь конец? Причем конец достаточно скорый. Во-первых, потому что следующее поколение фундаментальных теорий будет интересно все меньшему числу людей. Во-вторых, потому что рушатся надежды на построение огромного здания науки, в котором этажи, закоулки, подвалы и чердаки каким-то образом соединены друг с другом. Хотелось бы, находясь в одной части здания, знать, что при большом желании всегда можно попасть в другую. Пока это невозможно.
Поэтому, чтобы сохранить Игру, игрокам в бисер, вероятно, надо спуститься в мир и посмотреть на те задачи, которые волнуют простых смертных. Посмотрим на них и мы, обращая внимание на роль, предназначенную на этих подмостках Хаосу.
В качестве первой задачи можно назвать альтернативную, или теоретическую историю. В России сейчас меняется не политическая траектория, не лидеры и партии. Меняется не экономическая траектория, не курс доллара. Меняется не социальная траектория, в результате чего громадные социальные группы становятся «ничем». Речь идет о большем. Об изменении исторической траектории. И поскольку выбирать приходится между плохим и очень плохим вариантом, важно представлять, что нас ждет в одном, в другом, в третьем случае.
Естественные науки не имеют техники для такого анализа. Их про это просто не спрашивали. Гуманитарные науки имеют слишком много подходов, прекрасно согласующихся с тем, что пишут в газетных передовицах, и тем, что нужно для ближайших выборов. А опираться, как говорил Наполеон, можно только на то, что оказывает сопротивление.
Поэтому речь идет о разработке междисциплинарного подхода, позволяющего анализировать альтернативные исторические траектории и долговременные последствия принимаемых решений. Роль динамического хаоса и компьютерных технологий здесь принципиальна. В нынешнем быстро меняющемся мире горизонт прогноза резко сократился. Если раньше и в странах с плановой, и в странах c рыночной экономикой имели дело с пятилетними планами, то сейчас трудно планировать даже на полгода. В мире стало много «быстрых денег», которые могут быть вложены в проекты, дающие немедленную прибыль, и мало «медленных». Но, с другой стороны, чтобы плыть по реке, тем более, бурной, надо видеть другой берег или какие-то надежные ориентиры. Большой корабль безопасно может совершать только достаточно медленные повороты. Эволюция имеет много преимуществ перед революцией. Поэтому грядущие перемены следует предупреждать и готовиться к ним. Мать упрекала Марию Антуанетту за то, что она не оценивает возможности крутых поворотов, не думает о революции. Важно, чтобы нынешнее поколение ученых, в том числе и «нелинейщиков», не заслужило подобного упрека. Компьютерные технологии позволили создать огромные базы данных. Осталось понять, что с большинством из них делать. Важно, чтобы они «сыграли» не только в сиюминутных компьютерных делах, но и в той крупной игре, в которую сейчас играет наша цивилизация.
Другую сверхзадачу часто называют нейронаукой. Человек оказался совсем не тем, что о нем думали Просветители. Они полагали, что знание позволит действовать разумно. Однако XX век показал, что высокий технический уровень, огромный объем перерабатываемой информации не избавляет общество от войн, конфликтов, терроризма. Один известный психолог назвал одним из главных в своей науке простейший, на первый взгляд, вопрос — почему люди готовы действовать во вред себе и согласны жить на помойке? У Просветителей была неверная модель человека.
Но человек оказался загадкой не только в социальном, но и в техническом смысле. Скорость передачи информации в нашей нервной системе в миллион раз ниже, чем в персональном компьютере. Время срабатывания нервной клетки — нейрона — также в миллион раз превышает время такта персоналки. Очевидно, что при анализе работы мозга речь должна идти о других принципах, отличных от простейших компьютерных парадигм.
Важно отдавать себе отчет, что мы в этой области пока не умеем отвечать на простейшие вопросы. Где и как организовано хранение информации? Для чего нужен сон и можем ли мы без него обойтись? Каковы алгоритмы, по которым мы редактируем и забываем информацию? Почему младенец без труда отличает кошку от собаки, в то время как для компьютера это пока непосильная задача?
Нейронаука ищет ответы на эти вопросы на стыке вычислительной техники, когнитивной психологии, нейробиологии, нелинейной динамики. Роль хаоса здесь представляется очень важной. Головной мозг, как и многие другие системы организма, работает в хаотическом режиме. Недавно появившаяся теория управления хаосом говорит, что это дает нам множество интересных возможностей. Кроме того, нелинейщики активно учатся анализировать энцефалограммы. Но это лишь тусклый отблеск тех успехов, которые понадобятся в будущем.
Третья сверхзадача для науки XXI века пока не имеет короткого и красивого названия.
Условно говоря, это теория риска и безопасности. В полный рост проблема встала лет пятнадцать назад, хотя ее появление предсказывал еще в шестидесятых годах Станислав Лем в книге «Сумма технологии». Блаженный Августин, обсуждая в IV веке основы современного ему общества, создал труд «Сумма теологии». Мы живем в технологической цивилизации. В основу вместо теологии положены технологии.
Посмотрим на достигнутое со скромностью и смирением, как советовал Августин. Наши технологические успехи действительно весьма скромны. Трехкратное повышение урожайности зерновых в этом веке было оплачено увеличением потребления энергии в 100 раз на каждую тонну зерна. Произошли катастрофы на атомных станциях, надежность которых еще недавно оценивали 10-6 аварий/год, то есть одна авария в миллион лет. За последние тридцать лет число природных и техногенных бедствий с большим экономическим ущербом возросло вчетверо.
Билл Гейтс назвал глобальную систему телекоммуникаций «информационной нервной системой». Без нее сейчас немыслимо существование фондовых рынков. Но у этой системы есть свои болезни. В России это особенно понятно, поскольку за последние месяцы большинство наших сограждан стало, как минимум, втрое беднее. Все опаснее становится обслуживающая нас инфраструктура. Число аварий на магистральных трубопроводах в России растет примерно в полтора раза каждые два года. Мы живем в посткатастрофическом мире.
Ну и что? Казалось бы, это техническая, в лучшем случае, прикладная задача. Но это не так. У нас на физтехе первокурсникам объясняют, что все проблемы делятся на научные и технические. Технические заведомо имеют решение. Дело только в том, сколько оно стоит, кем и как оно будет получено. А научные проблемы могут как иметь решение, так и не иметь. Так вот, будущее нашей технологической цивилизации стало научной проблемой. Мы вступили в далекую закритическую область параметров, где еще никогда не бывали.
УПРАВЛЕНИЕ РИСКАМИ, ИЛИ ГРОЗНЫЙ МИР ВОСТОЧНЫХ СКАЗОК
Да, человек смертен, но это было бы еще полбеды. Плохо то, что он иногда внезапно смертен, вот в чем фокус!
М.А. Булгаков. «Мастер и Маргарита»
Лет тридцать назад Ричарда Фейнмана спросили: «Если бы завтра все живущие ныне физики погибли и от всех них в будущее можно было бы передать только одну фразу, что бы вы сказали?» «Весь мир состоит из атомов и пустоты, — ответил Фейнман. — Остальное они додумают».
Если бы такой же вопрос сейчас был задан всем ученым, а не только физикам, вероятно, фраза должна была бы быть иной: «Научитесь управлять рисками». Управление рисками- одна из важнейших технологий нашей цивилизации. Вообще, это магистральный путь прогресса — менять одни угрозы и опасности на другие. Например, опасность голодать и мерзнуть — на риск пожинать плоды заражения воды, земли, воздуха, связанные с работой тепловых или атомных станций. Возможность знать и видеть происходящее за тысячи километров, о чем не раз мечтали в сказках, оказалась связана с жизнью посреди информационного шума, среди рекламно-информационной свалки, океана лжи, слухов, домыслов. Видно, действительно бесплатный сыр бывает только в мышеловке.
Не надо думать, что здесь «иного не дано», как еще недавно твердили нам политики, что здесь можно только плыть по течению. Иное дано. Швеция приняла решение отказаться от атомной энергетики, как от слишком опасной технологии. В то же время во Франции, где более 70 процентов электроэнергии производится на АЭС, многие рассматривают форсированное развитие этой отрасли как важнейший способ сохранения окружающей среды. Ставки в этой игре весьма высоки, и свобода маневра достаточно велика.
Глубокая связь между идеями нелинейной динамики и управлением рисками стала ясна недавно. Осознать ее помогла парадоксальная статистика аварий. Вспомним «Титаник», «Челленджер», Чернобыль, Тримайл, Бхопал… Каждая из этих крупнейших катастроф XX века связана с длинной целью причинно-следственных связей с «неблагоприятным стечением многих маловероятных случайных обстоятельств», как часто пишут в актах государственных комиссий. И в самом деле, вздумай злоумышленник специально сделать что-то подобное, ему пришлось бы трудно. При знакомстве с бедствиями не оставляет чувство, что нам просто очень не везет.
Что же является математическим образом этого «невезения»? Выше уже звучало слово «случайность». «Король математиков», как его называли современники, Карл Гаусс установил, что сумма независимых, одинаково распределенных случайных величин подчиняется вполне определенному закону. Соответствующая ему кривая, получающаяся после нормировки, показана на рис. 3. Видно, что она очень быстро убывает, большие отклонения, в соответствии с этим законом, очень редки. Настолько редки, что ими можно пренебречь.

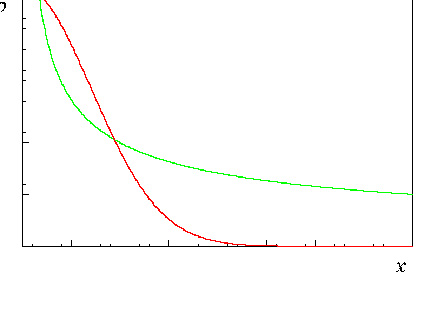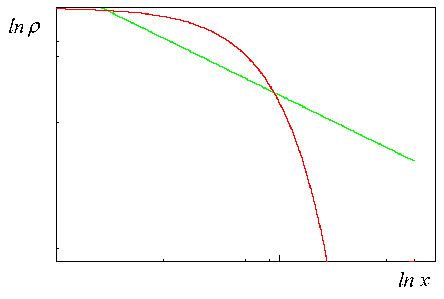Рис. 3. Классическим, привычным является гауссово распределение (оно показано красным). В соответствии с ним, большие отклонения настолько редки, что ими можно пренебречь. Однако многие бедствия, аварии, катастрофы порождают статистику со степенным распределением (оно показано зеленым). В этом случае редкими катастрофическими событиями пренебречь нельзя.
Простой пример: по этому закону распределен рост людей. Не знаю, как читателю, а мне трехметровых гигантов встречать не приходилось. Поэтому вероятностью такой встречи я с легким сердцем пренебрегаю.
Но есть и другой класс законов, которые называют степенными (красная кривая на том же рисунке). Здесь «хвост» убывает гораздо медленнее, поэтому такие законы часто называют «распределениями с тяжелыми хвостами», так что большими отклонениями тут пренебречь нельзя. Если бы по такому закону был распределен рост, то это был бы уже мир восточных сказок с тридцатиметровыми джиннами, ифритами, дэвами, которые вполне могли встретиться в жизни простых смертных.
Именно в мире восточных сказок мы обычно и оказываемся, сталкиваясь с бедствиями, катастрофами, авариями. Такова статистика землетрясений, наводнений, ураганов, инцидентов с хранением ядерного оружия, биржевых крахов, ущерба от утечки конфиденциальной информации, многих других невзгод. И защищаться от них нужно совсем иначе, чем от обычных «гауссовых аварий». Среди последних можно выделить проектные (иногда возникающие), запроектные (которые бывают совсем редко) и гипотетические аварии (настолько редкие, что ими можно пренебречь). А в случае «степенных бедствий» надо рассчитывать на худшее. В случае землетрясений нужно не надеяться «на авось», а вести сейсмостойкое строительство. Другой пример: плотины Волжского каскада закрывают водохранилища, содержащие десятки кубических километров воды. Их разрушение может привести к возникновению волны в десяток метров высоты. Это сотни тысяч жизней. Такая вот гипотетическая авария.
Чтобы представить масштаб редких катастрофических событий, достаточно напомнить несколько эпизодов из истории XX века. При наводнении 1931 года на реке Янцзы в Китае погибло 1,3 млн. человек, при Тянь-Шанском землетрясении в 1976 году — около 650 тысяч. Наводнение в Бангладеш в 1970 году унесло более 500 тысяч жизней и оставило без крова 28 млн. человек.
Откуда же берутся степенные законы и грозный мир восточных сказок? Американские исследователи П. Бак, Ц. Танг и К. Вайзеннельд в 1978 году высказали простую гипотезу: случайные воздействия на взаимодействующие динамические системы могут привести к лавине, позволить одним костяшкам домино повалить другие.
Опасность лежит между динамикой, о которой шла речь вначале, и привносимой извне случайностью. Как сейчас говорят, на кромке хаоса. Это и стало основой теории самоорганизованной критичности- новой звезды нелинейной динамики. Среди ее приложений — поведение фондовых рынков, биологическая эволюция, землетрясения, движение по автобанам, трафик сообщений через компьютерные сети и многие другие.
Теория управления рисками поставила перед специалистами по хаосу, компьютерному моделированию, работе с большими массивами данных еще одну интересную задачу. Условно ее можно назвать анализом длинных причинно-следственных связей.
Начнем и здесь со сказки. В тридевятом царстве, в тридесятом государстве произвели полезный и безопасный химический продукт для холодильников и аэрозольных баллончиков. Заводы построили, сеть сбыта организовали, прибыль получать начали. И вдруг оказывается, что, как убеждают тамошние мудрецы, разрушает хваленый продукт озоновый слой на высотах в 10-20 километров. И так ловко, что одна молекула чудо-вещества миллион озоновых в распыл пускает. А без озонового слоя в биосфере, если она, конечно, останется, наш биологический вид может оказаться лишним. И стали думать добры молодцы, по карману ли им отказаться от чудо-технологии…
Теперь несколько уточнений. Речь идет о хлорфторуглеродах, или фреонах. Отказываться от них решили в Монреале в 1992 году. И обойтись это должно более чем в 12 млрд. долларов. За непонимание длинных причинно-следственных связей приходится платить очень дорого.
А есть и другие, гораздо более опасные связи. Мы оперируем сейчас такими временными и пространственными масштабами, с которыми никогда не имели дела раньше. Нужна техника, а может быть, даже индустрия компьютерного анализа, на выходе которой должно быть предупреждение о будущих угрозах. Чтобы дальше царствовать спокойно, нужен золотой петушок.
И еще, пожалуй, одна картинка, показывающая, что самые разные катастрофические события могут развиваться по одним законам — а это и загадка, и надежда на разгадку. Речь идет о сложно организованных иерархических системах. В частности, о фондовых рынках и геологических объектах, отвечающих за сейсмическую активность.
На рис. 4 сверху по оси ординат отложен логарифм изменения индекса Доу-Джонса, по оси абсцисс — время. Здесь показан период перед Великой депрессией 1929 года. Индекс Доу-Джонса является одним из главных индикаторов состояния экономики. Грубо говоря, он характеризует среднюю рыночную стоимость одной акции. Снизу — концентрация ионов хлора в родниках в период подготовки землетрясения в Кобе. Обе кривые очень похожи, обе описываются с высокой точностью одной формулой. И, видимо, за этим сходством кроется аналогия между механизмами обоих явлений, возможность перенести методы прогноза из одной области в другую. Возможно, это ключ к разгадке.

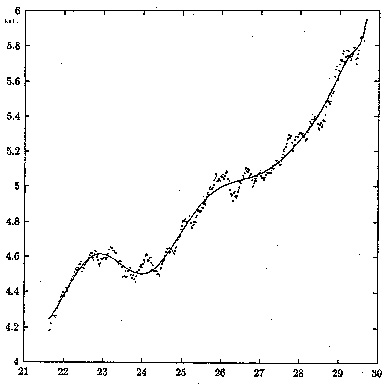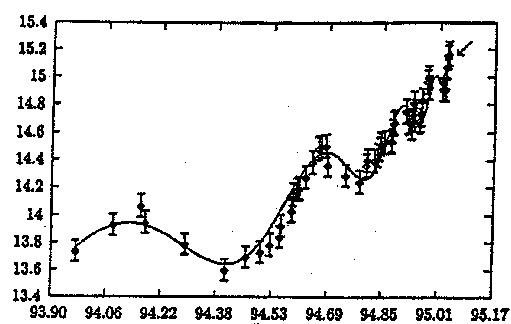Рис. 4. Слева — зависимость логарифма индекса Доу-Джонса от времени перед Великой депрессией 1929 года. Справа — зависимость концентрации ионов хлора в родниках перед землетрясением в Кобе в 1995 году.
И еще одна задача. Допустим, что мы живем в 1927 году и знаем, что ждет американцев через два года. Что предпринять? Как уберечь людей от беды? Это проблема социума, направляемого развития, воздействия на общественное сознание.
Работа с информацией, основанная на компьютерных технологиях, глобальные телекоммуникации — сегодня главные козыри при управлении риском. Во-первых, потому, что каждая катастрофа должна учить. В XX веке у каждой катастрофы были «предтечи» — аварии того же типа, но меньшего масштаба. И чтобы предупредить «премьеру», надо на основе скромной «репетиции» менять нормы, планы, правила игры в социуме и техносфере. Лучше вложить тысячу в прогноз и предупреждение аварии, чем миллион в ликвидацию ее последствий. Во-вторых, информация и прогноз позволяют спасать тысячи жизней, сокращая время реагирования на события. В-третьих…
Впрочем, здесь надо остановиться. Работы, которые сейчас ведутся в Институте прикладной математики им. М.В. Келдыша РАН и в ряде академических институтов по инициативе Министерства по чрезвычайным ситуациям в России, показали, что здесь есть огромное поле деятельности, на котором Хаос занимает ключевое положение.
РУСЛА И ДЖОКЕРЫ
Природа, чем она ни будь,
Но черт ее соавтор -
Вот в чем суть.
И. Гете. «Фауст»
Вернемся к динамическому хаосу. Спросим: если предсказывать, даже с помощью современных компьютерных технологий, так непросто, то как же нам удается ориентироваться в нашем сложном и быстро меняющемся мире? Как удается разумно действовать, несмотря на свой весьма скромный горизонт прогноза?

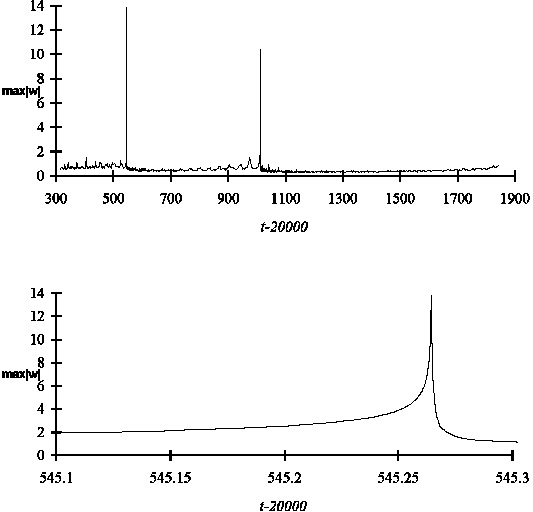Рис. 5. Возникновение и распад пика

Здесь видно пришла пора сказать о грантах РФФИ и научной биографии. Всю мою научную жизнь я имел честь работать в Институте прикладной математики им. М.В. Келдыша и занимался синергетикой и нелинейной динамикой. При этом приходилось сталкиваться со многими интересными задачами от лазерной термохимии и солнечного динамо до описания высшей школы и моделирования исторических про-цессов. Все эти задачи объединяла необходимость находить параметры порядка в поведении сложных систем и прогнозировать их судьбу.
Именно такой «тяжелый» системе и методам ее анализа и был посвящен грант Российского Фонда Фундаментальных Исследований 97-01-00396, которым мне довелось руководить. Эта система описывает так называемую «жесткую турбулент-ность» — явление при котором в какой-либо системе на хаотическом фоне иногда возникают гигантские всплески. Примерно так как на рис. 5. Почему? Можно ли объяснить это на пальцах? Можно ли предвидеть «катастрофу»? Явление жесткой турбулентности было открыто в 70-е годы в физике плазмы. Позже такие же уравнения писали в теории ветровых волн на воде, в химической кинетике, в математической биологии и еще многих других областях. Однако ответов на поставленные вопросы не было.
В новой парадигме нелинейной динамики исследовавшаяся модель жесткой турбулентности может стать одной из основных. Дело не только в том, что это очень «неудобная задача» для вычислительного эксперимента — важные события разворачиваются в сокращающейся области пространства. Не только в том, что здесь есть малые параметры, значение которых очень велико. Не только в том, что асимптотикой роста возникающих структур является режим с обострением, при котором изучаемые величины за конечное время достигают бесконечных значений (такие режимы в Институте прикладной математики им. М.В. Келдыша детально исследовались в научной школе С.П. Курдюмова в связи с задачами теории горения и физики плазмы). Принципиально важен вопрос, — можно ли это явление, описываемое весьма сложной системой уравнений для бесконечного числа степеней свободы, смоделировать предельно просто. Если да, то можно надеяться, что удастся удачно упростить и в других случаях. Если нет… То надо думать дальше.
Забегая вперед, могу сказать, что благодаря настойчивости и изобретательности С.В. Ершова и А.Б. Потапова удалось получить положительный ответ. Жесткую турбулентность удалось описать настолько просто, что численный анализ упрощенной системы сейчас можно поручить второкурснику Физтеха. В проекте же многое удалось сделать аналитически и с удовлетворением сравнить работу компьютера с тем, что получилось на бумаге.
Однако вернемся к общему вопросу — как все же удается что-то предсказывать, несмотря на небольшой горизонт прогноза. Попытки получить на него ответ, а с ним и алгоритмы прогноза, предпринимаются в создаваемой сейчас теории русел и джокеров.

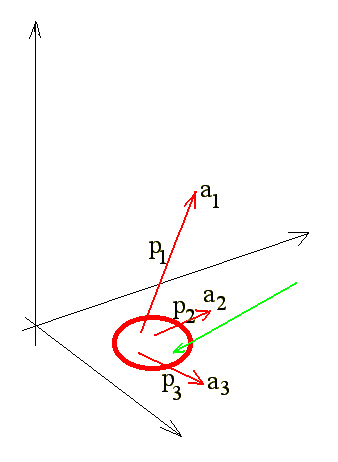
Рис. 6. Картинка, возникающая в задаче с разорением банка. Небольшая красная область соответствует области джокера, в которой надо принимать серьезные меры.

Одним из ее авторов по праву может считаться известный финансист Дж. Сорос. В своей «Алхимии финансов» он выдвинул идею «информационной», или «рефлексивной», экономики. В соответствии с ней такие переменные, как «уровень доверия», «ожидаемые прибыли» и многие другие, характеризующие нашу «виртуальную реальность», играют ключевую роль в современной экономике. Именно они позволяют строить, а затем уничтожать величественные финансовые пирамиды, такие как МММ, «Чара», «Тибет», ГКО… Но именно эти переменные могут меняться скачком, что совершенно не характерно для математических моделей, построенных в естественных науках.
Другими словами, в фазовом пространстве многих объектов, с которыми мы имеем дело в жизни, есть места, называемые областями джокеров, в которых случайность или игровой элемент, или фактор, не играющий никакой роли в другой ситуации, может оказаться решающим и не только повлиять на судьбу системы, но и скачком перевести ее в другую точку фазового пространства. Правило, по которому совершается этот скачок, и называется джокером. Название пришло из карточной игры. Джокер — карта, которой можно присвоить значение любой карты по желанию играющего. Понятно, что это резко увеличивает число вариантов и степень неопределенности.
Простой пример. Допустим, у нас с вами есть небольшой банк. И дела день ото дня идут все хуже. Да и как может быть иначе в эпоху кризиса? Пора принимать решение. Первое, наиболее естественное (оно принимается с вероятностью p1, см. рис. 6) — организовать презентацию в «Хилтоне». Шумиха, журналисты, новые клиенты и возможности. Второе — поступить, как честные люди, и объявить о банкротстве (вероятность p2). Наконец, подумать о семье и близких друзьях и улизнуть, прихватив всю оставшуюся наличность, чтобы с другого берега океана поучать местных реформаторов (вероятность p3). Видим, что у нас вновь и вновь возникает симбиоз динамики, предопределенности и случайности.
Можно перевести сказанное на медицинский язык. Вдали от области джокера эффект должна давать терапия, а в самой области нужно гнать терапевтов и звать хирургов. И ситуация при этом может измениться быстро и радикально.
С помощью представлений о джокерах можно говорить и о старых знакомых, динамических системах. Иллюстрацию, показанную на рис. 7, придумал сотрудник ИПМ им. М.В. Келдыша РАН И.В. Фельдштейн.

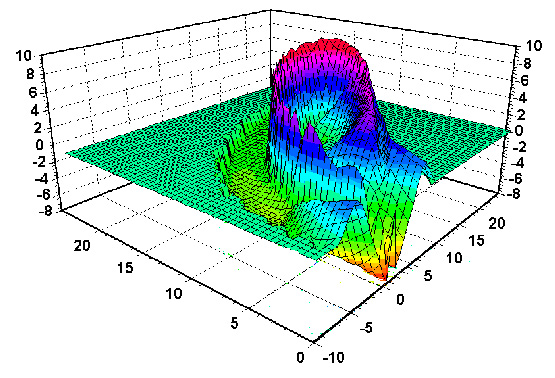Рис. 7. Локальные скорости разбегания (сходимости) для аттрактора Лоренца. Области выше нулевого уровня соответствуют разбеганию, ниже нулевого уровня — сходимости. Видно, что первые занимают сравнительно малую часть.

Речь опять идет о системе Лоренца. Цветом на рисунке показана скорость, с которой траектории разбегаются (область выше нулевого уровня) или сходятся (область ниже нулевого уровня). Видно, что область разбегания, которой естественно сопоставить джокер, довольно мала.
Но если нам не везет с прогнозами в области джокера, то где-то должно и везти. Подумаем: что значит «везет с прогнозом»? Это значит, что поведение системы с устраивающей нас точностью определяется лишь несколькими переменными, а обо всем остальном в первом приближении можно забыть. Кроме того, здесь должна быть возможность предсказывать на довольно большой срок. Такие области в фазовом пространстве и были названы руслами.
Вероятно, способность эффективно выделять русла, учиться не только методом проб и ошибок, совершенствуя свою предсказывающую систему и здравый смысл, и дала нашему виду решающее преимущество в ходе эволюции. Можно взглянуть и более широко: разные теории, подходы, науки оказываются полезными и востребованными, если они удачно нашли свои русла. Ведь наука — это искусство упрощать, а упрощать особенно удобно, имея дело с руслами. Разумеется, «в среднем», «в общем случае» мы не можем заглянуть за горизонт прогноза. Но «в частности», оказавшись в области параметров, соответствующих руслу, и осознав это, можно действовать разумно и осмотрительно.
Но тут возникает вопрос: где начинается и где кончается русло? Какова структура нашего незнания? Как от одного информационного поля и одних представлений, адекватных этому руслу, переходить к другим, когда это русло кончилось? Знакомясь с разными экономическими, психологическими, биологическими теориями, трудно отделаться от ощущения, что, сами того не осознавая, их создатели имеют дело с разными реальностями, с разными руслами. Это сродни дополнительности в квантовой механике, когда ответ на вопрос, является электрон волной или частицей, зависит от конкретного эксперимента.
А теперь вернемся от общего к частному. К жесткой турбулентности.
Кроме компьютерного моделирования, построения упрощенных моделей, дающих понимание этого замечательного явления и использующих представления о руслах и джокерах удалось обнаружить еще одну интересную вещь. Это предвестники — медленно меняющиеся переменные, которые свидетельствуют о приближении катастрофы. Они показаны на рис. 8. Их оказывается достаточно просто посчитать. И увидеть после этого, что угроза приближается. Глядя на их изменение, нельзя точно

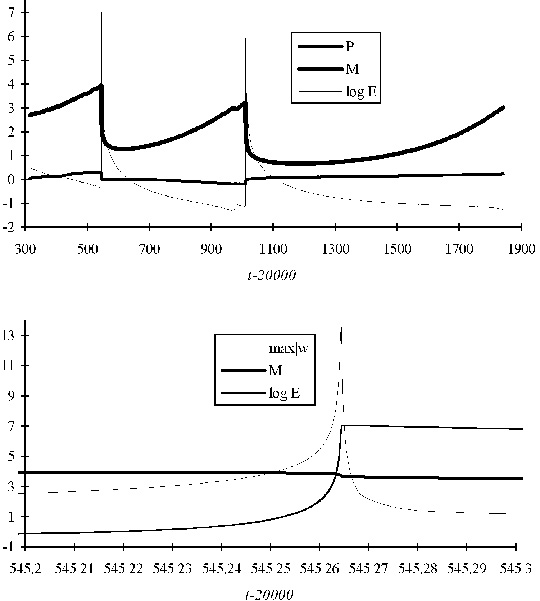Рис. 8. Изменение медленных переменных перед гигантскими пиками

сказать, когда нас ждет гигантский выброс, но об опасности они сигнализируют. По-видимому, такая ситуация характерна и для многих других систем, в которых возможны катастрофические явления.
Интересно, как удалось найти эти медленные переменные… Впрочем здесь начинаются подробности, дорогие сердцу автора, и в популярной статье неуместные. Внимание интересующихся подробностями обращу к списку литературы в конце. И еще хотелось бы, чтобы читатель не воспринимал историю с анализом катастроф как «хэппи-энд». Скорее это обнадеживающее начало.
…На одной конференции по искусственному интеллекту была дана такая форму-лировка. Простые задачи — это те, которые легко решить или доказать, что они неразрешимы, остальные задачи — сложные. Развитие представлений о хаосе, и их применение в разных областях показывают, что нам повезло. Конструирование будущего, осмысление новой реальности, сущности человека, алгоритмов развития и управления оказалось сложной задачей.
Литература
1. Новое в синергетике. М.: «Наука», 1996.
2. Капица С. П., Курдюмов С. П., Малинецкий Г. Г. Синергетика и прогнозы будущего. М.: «Наука», 1997.
3. Малинецкий Г.Г. Синергетика. Король умер. Да здравствует король! http://www.iph.ras.ru:8101/~mifs/rus/malin1r.htm
4. Малинецкий Г.Г., Потапов А. Б. Катастрофы и бедствия глазами нелинейной динамики// Знание-сила. 1995. №3, с.26?34.
5. Малинецкий Г.Г. Нейроромантизм или компьютерные вариации на темы мозга// Знание-сила. 1994. №8, с.44?50.
6. Пределы предсказуемости. М.: «Центрком», 1997.
7. Sornette D., Johansen A. Large financial crashes. Physica A. 1997. V.245, N34, p.411?422.
8. Johansen A., Sornette D., Wakita H., Tsunogai U., Newman W.I., Saleur H. Discrete scaling in earthquake precursory phenomena: Evidence in the Kobe earthquake, Japan// J. Phys. I France. 1996. V.6, p.1391?1402.
9. Малинецкий Г.Г. Хаос. Структуры. Вычислительный эксперимент. М.: УРСС, 2000.
10. Малинецкий Г.Г., Потапов А.Б. Современные проблемы нелинейной динамики. М.: УРСС, 2000.