Применение нелинейной динамики в науках о жизни — общего синергетического подхода или математического моделирования — открыло возможность дальнейшего поиска универсальных тенденций в поведении сложных динамических систем. Специалисты разных предметных областей с трудом договариваются о междисциплинарных аналогиях при получении сходных эффектов и феноменов, и в этом смысле развитие системного подхода, синергетического языка, теории сложности, теории хаоса, теории динамических систем или теории катастроф помогает развитию новых аналитических средств и современной философии. Рассмотрим конкретный пример моделирования социального поведения.

1. Общие признаки популяционных систем

Применение нелинейной динамики в науках о жизни — общего синергетического подхода или математического моделирования — открыло возможность дальнейшего поиска универсальных тенденций в поведении сложных динамических систем. Специалисты разных предметных областей с трудом договариваются о междисциплинарных аналогиях при получении сходных эффектов и феноменов, и в этом смысле развитие системного подхода, синергетического языка, теории сложности, теории хаоса, теории динамических систем или теории катастроф помогает развитию новых аналитических средств и современной философии. Рассмотрим конкретный пример моделирования социального поведения.

Социологи и историки при описании процессов формирования и распада больших социальных образований основное внимание уделяют конкретным экономическим условиям, политическим играм и жизни реальных лиц. Социобиологи и этологи описывают социальное поведение конкретных биологических видов и при попытке провести какие-то аналогии с поведением людей встречают мощное сопротивление психологов. Социальные психологи с гордостью причисляют к социально-психологическим феноменам явления конформизма, группового заражения, групповой идентификации, зависимости поведения людей от размера группы и т.п. Психологи исписали тонны бумаги о взаимодействии между социальными условиями и биологическими предпосылками индивидуального поведения. Все согласны, что поведение осуществляется не только согласно внутренним чертам человека, но также при системном эффекте социального окружения. Однако в психологии личности, возрастной и педагогической психологии и психиатрии социальное окружение рассматривается в основном в плоскости влияния конкретных людей, вступающих в контакт с субъектом. (Пожалуй, только в школе К.Левина (K.Levin, 1936) была сделана попытка проанализировать динамические тенденции, не зависящие от индивидуальных особенностей участников взаимодействия).

Каждый из этих специалистов говорит на своем языке и каждое такое описание является качественным описанием. Можем ли мы, однако, подключить к нему количественный анализ этих процессов?

Рассмотрим, что объединяет все живые системы, и как мы реализовали эти свойства в своих моделях.

• Многоагентность, «коллективная» природа естественных систем: все они представляют собой многоэлементные среды и демонстрируют системные эффекты, не сводимые к относительно простым закономерностям, описывающим поведение отдельных элементов. Многоагентность определяет то, что при взаимодействии системы со средой основную роль играют не абсолютные значения признаков, определяющих это взаимодействие, а относительные, т.е. ранг элемента по этому признаку в отношении других элементов. Это свойство моделировалось нами с помощью клеточных автоматов , при этом проводилось ранжирование элементов по определенным признакам на каждом шаге и подсчеты осуществлялись на основе рангов. Кроме того, проводился анализ получаемых эффектов для клеточных популяций разных размеров.
• Неоднородность, разнообразие элементов внутри системы, что моделировалось разнообразием клеток внутри популяции (задавались параметры: число признаков и степень разброса значений по ним).
• Динамичная структурность, при которой структура имеет гибкий, меняющийся состав, но сохраняет основные свои признаки, несмотря на то, что составляющие структуру элементы были заменены. Тем самым нелинейность развития психологических систем определяет многоальтернативность проявления их свойств: элемент, ввиду изменения своего ранга в популяции может кардинально изменить структуру связей и входные/выходные потоки ресурсов через себя, имея при этом неизменные формальные параметры. Его ранг в популяции может меняться исходя из изменения окружения, при этом система поставит его на другое место, а его место займет другой элемент. Практически это — начало системного подхода, когда структура описывается не как обособленная система, а как временно структурированная определенным образом часть более глобальной системы, развивающейся по своим законам, и при этом свойства элемента системы определяются его местом в структуре. Психология так же декларирует системные принципы описания своих объектов, однако используемая этими науками старая методология жесткой структурности мира оказывается сильнее.
• Открытость системы, наличие некоторого притока ресурса, капающего в систему на каждом шаге. Происхождение этого ресурса не уточняется, но он может быть как внешним, так и внутренним, появляющимся в результате эффективной внутренней организации, позволяющей высвобождать так называемую «свободную энергию».
• Диссипативность, траты ресурсов системой, которые могут трех типов: пустыми тратами, тратами на самоизменение и тратами ресурса, уходящего по связям с другими системами.
• Интегрированность, возможность взаимодействий в системе, число связей, которые элементы могут установить с другими, что может зависеть от таких факторов, как отдаленность элементов друг от друга (плотность) и возможности их контактов (социабельность).

Применительно к психологии, нами использовалось представление о человеке как, с одной стороны, субъекте отношений в сообществе и, с другой, как некоем интегральном образовании с собственными формально-динамическими характеристиками, отражающими особенности потребления и производства энергетических и информационных ресурсов. Задавалась ситуация, когда клетка получает жизненный ресурс в зависимости от совместимости интересов с теми, с кем у нее установлены связи: чем больше совместимость, тем больше ресурса она получает. Потенциально она могла установить связь с любым элементом популяции, однако количество контактов на одном шаге ограничивалось.

2. EVS-моделирование

Как уже было упомянуто в сноске, назвать наши модели клеточными автоматами можно только условно, они ближе к структуре случайных графов, однако также отличаются от них. Предлагаемый нами общий подход к моделированию мы называем EVS-модели (Ensambles with Variable Structure), то есть ансамбли с переменной структурой. Были разработаны модели «Социабельность» (Трофимова и др., 1997, Trofimova at al, 1998), «Адаптация» и «Функциональная дифференциация» (Trofimova, Mitin, 1998). Главными отличительными чертами EVS-моделей являются следующие:

• Во-первых, в традиционных моделях берутся дискретные характеристики клеток с относительно небольшим спектром значений. В наших моделях клетки отличаются друг от друга в гораздо большем спектре значений, что делает характеристики практически непрерывными и позволяет анализировать второй из указанных моделируемых признаков — разнообразие элементов.
• Во-вторых, в традиционных клеточных автоматах связи между клетками локальные и фиксированные, в то время как в нашей модели клетки могут устанавливать какие угодно связи по всей популяции и перестраивать структуру связей. Подобная гибкость моделировала признак динамичной структурности, т.е. изменчивости состава образующихся систем при сохранении структуры.
• Третьим отличием разработанных моделей от традиционных клеточных автоматов было то, что клетка не сидит в пассивном ожидании, пока сосед наконец умрет или оживет, как, например, в игре «Жизнь» Конвея, а «работает» с потоком некоторого жизненного ресурса, который либо «капает» на нее извне, либо она сама продуцирует ресурс и тратит его. Это позволило смоделировать диссипативность (через траты ее ресурса) и открытость самой клетки (через поступления ресурса). Кроме того, сама популяция как открытая и диссипативная система также получала и тратила некий ресурс, что выражалось в случайном распределении приходящего к конкретной клетке ресурса на каждом шаге, который мог быть отрицательным (т.е. представлять по сути дела трату).

3. Модель «Социабельность»

В рассматриваемой модели ставился вопрос о влиянии на поведение в группе таких формальных признаков среды, как величина популяции, возможности установления контактов (социабельность) и степень разнообразия элементов популяции. Время жизни популяции было дискретным, т.е. пошаговым: от 2000 шагов для малых популяций и 5-10 тысяч шагов для больших. На каждом шагу клетка предпринимала попытку оптимизировать структуру своих связей — найти кого-нибудь более совместимого и расторгнуть связь с менее совместимым. При этом разнообразие клеток задавалось вектором в пространстве абстрактных характеристик с помощью модели взаимодействующих спинов (подробнее см. Трофимова и др., 1997; Trofimova, 1998; Trofimova et al, 1998).

Было исследовано более 300 различных случаев — с разной величиной популяций (от 20 до 2000) и социабельностью, т.е. возможностью установления контактов (от 5 до 400 для больших популяций).
Помимо других интересных эффектов это исследование показало наличие как минимум одного основного фазового перехода второго порядка (т.е. качественного перехода от одного состояния к другому, подобно тому, как лед тает до состояния воды, а вода при определенных условиях переходит в пар). Основным объектом анализа стала динамика формирования групп (или кластеров), в которые объединяются элементы.

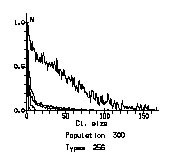
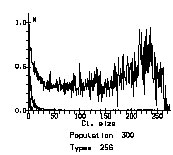
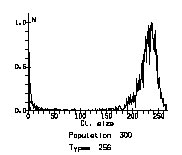
Несмотря на то, что связи каждой конкретной клетки были достаточно динамичными, модель продемонстрировала наличие устойчивого статистического поведения — разное распределение кластеров определенного размера при разных значениях параметров. Рисунок 1 показывает примеры распределения размера кластеров до, во время и после перехода к качественно разному поведению: в первом случае мы имеем много малых группок и небольшое число больших кластеров — что, собственно, наблюдается в поведении слабоинтергированных систем — объединение популяции по одному-двум признакам, тогда как по всем другим признакам каждый делает что хочет и как хочет.
После перехода, однако, «разброд» в популяции резко сокращается — она превращается в интегрированную систему, где, по мере увеличения возможности поддержания контактов растет запрет на малые группы — все элементы контролируются малым числом больших кластеров.

a) Sociability 15	b) Sociability 40	n) Sociability 90
Рис.1. Функции распределе- ния кластеров. Ось y пока-зывает число кластеров, нормализованное по моде

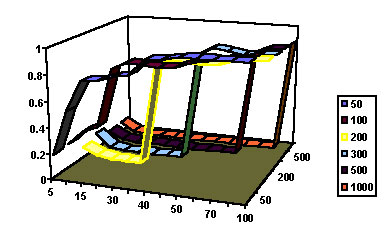
Поведение, связанное с принад-лежностью к той или иной группе обычно называют аффилиативным, поэтому мы назвали имеющийся здесь параметр порядка аффилиацией (А). Рисунок 2 показывает распределение А как функцию от размера популяции и социабельности (по оси y — размер популяций, по оси х — социабельность, по оси z — аффилиация). Для малых популяций аффилиация растет более или менее монотонно, как функция от социабельности. Для больших популяций переход к другому поведению происходит более внезапно: например, для популяции в 300 элементов при изменении социабельности вплоть до 40 контактов аффилиация держится около 0.01, однако при числе контактов 41 размер кластеров делает скачок до 0.82 процента от всей популяции.

Вычисления энтропии для каждой функции распределения в каждой популяции и математических ожиданий позволило нам найти нелинейную зависимость, описывающую критическое значение социабельности (Sc) для перехода к качественно другому поведению, взятую от величины популяции (P): Sc=P0,6. Тем самым мы можем предсказать, какое критическое число контактов необходимо для того, чтобы любое данное множество клеток, элементов или людей пришло в упорядоченное состояние и стало системой.

Строго говоря похожие эффекты — но без подробного количественного анализа на дискретных моделях с разнородными элементами — были получены в теории случайных графов (Palmer, 1985), в теории перколяции (Grimmett, 1989). Структура связей между элементами, однако, в этих моделях была фиксированной, в то время как структура кластеров в нашей модели очень динамична — кластеры не существуют в одном и том же виде практически более, чем 10 шагов.

Рис. 2. Ландшафт параметра порядка «Affiliation». Линии показывают аффилиацию как функцию от размера популяций и социабельности

4. Психологические эффекты модели

Более интересно, однако, посмотреть на эти результаты с психологической точки зрения. Упомянутая «социабельность» является возможностью субъекта поддерживать определенное число контактов, а некоторая суммарная совместимость с теми субъектами, с которыми установлены контакты, показывает оптимальность использования этих контактов — обмен информацией и ресурсами, кооперацию (при положительной совместимости) или конфронтацию (при отрицательной). Социабельность может быть основана на индивидуальных чертах субъекта, но, как правило, среда задает некоторые пределы числу поддерживаемых контактов, поэтому «последнее слово» в установлении этого числа мы оставили за средой.

Аффилиативное поведение (когда субъект предпочитает быть членом определенной группы) и мера сходства поведения членов группы зависят, как оказалось, не только от индивидуальных предпочтений отдельного субъекта и даже не от установок других членов группы, а от более глобальных факторов — величины всех популяции, в которой происходит группировка, ее разнообразия и особенно — от возможностей поддерживать контакты.

На бытовом уровне это достаточно очевидный факт — чем больше я могу установить и поддержать контактов, тем больше обмен информацией и тем более едины мы в суждениях и поведении. Как используется этот факт в психодиагностике или социальной психологии? Пожалуй, в лучшем случае, в форме констатации. Однако мы можем использовать здесь и количественные закономерности: например, учитывать размер групп, в которые включен индивид и возможности поддержания контактов, фактическое число контактов, которые индивид поддерживает — для составления каких-либо заключений о его социальных способностях. В социальной психологии, при исследовании групповой динамики, мы можем также использовать полученную количественную зависимость для того, чтобы отделить ее влияние от собственно социально-психологических эффектов. Описанный нами эффект согласуется, как ни странно, и со стратометрической концепцией коллектива, предложенной А.В.Петровским (Петровский, 1979). Совместная деятельность, как фактор, объединяющий людей в коллектив, как правило сопровождается интенсивными реальными и виртуальными (через интериоризацию совместных задач) контактами.

Другое важное замечание — увеличение униформизма в поведении при повышении социабельности элементов. После фазового перехода мы видим, что большие кластеры как бы «подбирают под себя» малые группки и на развитой стадии перехода малых групп практически не существует. Этот эффект похож на явления тоталитаризма, монополизма или идеологического контроля, которые появились с развитием средств коммуникаций.

И, наконец, по полученным результатам можно сделать некоторые выводы об иерархии параметров, определяющих поведение. Мы рассматривали четыре таких системных фактора: размер популяции, разнообразие популяции, число контактов, которые элемент может «проверить на совместимость» на каждом шагу и максимальное число контактов, которые он может удерживать на каждом шагу (социабельность). Вопрос об иерархии этих параметров на самом деле является достаточно открытым для психологии: когда мы обсуждаем детерминанты поведения человека, можем ли мы с уверенностью сказать, что важнее — разнообразие социальной среды, величина групп, в которых он задействован, интенсивность контактов либо общее число действующих контактов?

Наше исследование показало, что величина популяции определяет наиболее глобальные тенденции в поведении, а общее число действующих контактов является основным фактором групповой динамики, совместно с величиной популяции задающим нелинейную функцию качественного перехода в поведении. Уменьшение интенсивности контактов (т.е. сколько контактов клетка может проверить на каждом шаге) увеличивает, как оказалось, «резкость» полученных эффектов и делает фазовый переход более явным. Разнообразие популяции оказалось четвертым в иерархии изучаемых параметров, однако оно тоже оказывало свой эффект: был также получен (но более слабый) фазовый переход в зависимости от этого фактора.

Эффекты, подобные полученным, говорят о том, что психология, как и другие науки о жизни, не должны «вариться в собственном соку» и объяснять одни психологические явления с помощью других психологических же явлений. Философия и математика, как достаточно философская дисциплина продолжают поиск универсальных тенденций в явлениях разной природы, но этот поиск будет успешен только при участии специалистов конкретных предметных областей науки. Социальные процессы, в частности, подчиняются глобальным законам внутренней динамики многоагентных сред, которые характеризуют все естественные системы (Sulis, 1994).

Автор выражает глубокую благодарность за программное обеспечение по данной работе А.В.Потапову, а также доктору Вильяму Сулису и за содержательные консультации по обработке данных.

ЛИТЕРАТУРА:

Петровский А.В. (Ред). Психологическая теория коллектива. М. 1979.
Трофимова И.Н., Митин Н.А., Потапов А.В., Малинецкий Г.Г. Описание ансамблей с переменной структурой. Новые модели математической психологии. Препринт N 34 ИПМ им.Келдыша РАН. 1997.
Grimmett G. Percolation. Berlin: Springer-Verlag. 1989.
Levin K. (1936) Principles of Topological Psychology. N.Y. 1936.
Palmer E. Graphical Evolution. New York, Wiley Interscience. 1985.
Sulis W. Causality in Naturally Occurring Computational Systems. World Futures. 39, 225. 1994.
Trofimova I. (1998). The definition of parameters for measurement in psychology. In: F.M. Guindani & G. Salvadori (Eds.) Chaos, Models, Fractals. Italian University Press. Pavia, Italy.
Trofimova I., Mitin N. (1998) Modeling of Group Interactions: Some Useful Concepts. Proceeding of the Conference Managing the Complexity, Toronto. In press.
Trofimova I, Potapov, A., Sulis, W. (1998) Collective Effects on Individual Behavior: In search of Universality. International Journal of Chaos Theory and Applications Pp.35-45.