Синергетика предлагает новую методологию для исследования сложных систем . Синергетический подход открывает возможности поиска универсальных принципов их самоорганизации и коэволюции. Такое знание исключительно важно для конкретного моделирования эволюционных процессов и катастрофических ситуаций в экономике и экологии, в социальной сфере и демографии.
На пороге третьего тысячелетия в условиях постоянного нарастания неустойчивости развития цивилизации всех нас волнуют вопросы о том, куда ведет эволюция, каковы исторические пути развития человечества и варианты будущего развития, каковы особенности и последствия происходящего ныне демографического взрыва, как избежать неблагоприятных, катастрофических ситуаций и каковы условия стабильного и безопасного развития человечества. Синергетика предлагает новую методологию для исследования сложных систем . Синергетический подход открывает возможности поиска универсальных принципов их самоорганизации и коэволюции. Такое знание исключительно важно для конкретного моделирования эволюционных процессов и катастрофических ситуаций в экономике и экологии, в социальной сфере и демографии.
Каждому историческому периоду в развитии науки свойственны свои специфические идеалы научного знания и методологические подходы к осмыслению действительности. В науке Нового времени — классической науке — идеалами научного знания служили простота, линейность, исключение неопределенности. Классический, господствующий по сей день подход к управлению сложно организованными системами основывается на линейном представлении об их функционировании. Согласно этому представлению результат внешнего управляющего воздействия есть однозначное и линейное, предсказуемое следствие приложенных усилий. Результат воздействия тем больше, чем оно сильнее.
Вместе с бурным развитием статистических теорий (теория игр, теория ошибок, статистическая физика, демография и пр.) происходил переход к вероятностному стилю научного мышления, статистические закономерности перестали рассматриваться как нечто временное и преходящее. Интенсивное развитие системных исследований и кибернетики привело к очередному изменению в стиле научного мышления.
Синергетический подход разширяет вероятностное видение мира, дополняя его такими важнейшими элементами, как сложность, системность, целенаправленность . Синергетика открывает необычные стороны мира: его нестабильность и режимы с обострением (режимы гиперболического роста, когда характерные величины многократно, вплоть до бесконечности возрастают за конечный промежуток времени), нелинейность и открытость (различные варианты будущего), возрастающую сложность формообразований и способов их объединения в эволюционирующие целостности (законы коэволюции).
Предельно краткая характеристика синергетики как новой научной парадигмы включает в себя три основные идеи: нелинейность, открытость, диссипативность.
- Нелинейность — необычная реакция на внешние воздействия, когда правильно организованное воздействие оказывает большее влияние на эволюцию системы, чем воздействие более сильное, но не оформленное адекватно ее собственным тенденциям.
- Открытость — наличие внешних источников и стоков, необходимое условие существования устойчивых неравновесных состояний (аттракторов системы), в противоположность замкнутой системе, неизбежно стремящейся, в соответствии со вторым началом термодинамики, к однородному равновесному состоянию.
- Диссипативность — хаотический характер элементарных процессов в системе, фактор «естественного отбора», разрушающий все, что не отвечает тенденциям развития, «молоток скульптора», которым тот отсекает все лишнее от глыбы камня, создавая скульптуру.
Именно нелинейные открытые диссипативные системы, повидимому, лежат в основе большинства физических, биологических, социальных явлений. Не случайно многие общие принципы эволюции можно отнести к самым различным объектам живой и неживой природы. Это и регенерация (восстановление собственной структуры, нарушенной внешним воздействием), и морфогенез, сопровождаемый своеобразным «дефектом массы», обуславливающим большую эффективность сложных структур по сравнению с простыми. Научная картина мира включает в себя принцип единства, проявляющийся в существовании законов, справедливых для самых разнообразных уровней существования, от микромира до Метагалактики, от неживой природы до человека и общества. В классической науке такими законами были, например, закон сохранения энергии, второе начало термодинамики… В современной постклассической науке ими могут стать законы коэволюции нелинейных открытых диссипативных систем.
Становится понятным, каким образом человек познает мир, если предположить, что мозг человека подчиняется тем же законом развития, что и окружающая его живая и неживая природа, но на более высоком уровне, характеризующемся большей нелинейностью, другим соотношением факторов открытости и диссипативности системы. Тогда мозг может создать внутри себя и исследовать модельные структуры, соответствующие структурам — объектам окружающего мира (имеющие общие законы строения и эволюции).
2. Синергетическая модель роста народонаселения.
Демография, подобно другим статистическим дисциплинам, долгое время использовала методы линейного моделирования. Зависимость скорости увеличения населения полагалась пропорциональной числу людей, откуда следовал экспоненциальный закон роста населения и постоянство относительной скорости роста. Однако давно было известно, что линейное приближение может быть использовано только на небольших участках временной оси, а в экспоненциальном законе нужно использовать меняющийся со временем коэффициент, отражающий изменение относительной скорости роста. Такой коэффициент обычно включает в себя параметры, изменяющиеся со временем (скорость их изменения полагается много меньше характерной скорости изменения численности населения). Это, например, — средняя продолжительность жизни, вероятность рождения ребенка у женщины определенного возраста, зависимость смертности от возраста. Эти параметры, как правило, содержат зависимости от ряда социальных, экономических, а также внешних по отношению к обществу факторов.
Демографические прогнозы, однако, в последнее время становятся менее точными, что обусловлено, прежде всего, существенным увеличением скоростей изменения упомянутых величин. Сегодня считается, что демографические прогнозы могут быть получены с достаточно высокой точностью только на периоды не более 40 лет, если же длительность прогноза превышает эти ограничения, точность прогноза уменьшается катастрофически. Так, различные прогнозы численности человечества на ближайшие несколько лет различаются в несколько раз.
В последние годы в демографии все шире стал применяться системный подход, в рамках которого население Земли рассматривается как «целеустремленная самоуправляющая система». Понятие целеустремленности понимается демографами как самоподдержание определенных законов развития этой системы, независимо, а иногда вопреки воздействиям на нее как извне (болезни, стихийные бедствия и пр.), так и изнутри (демографическая и социально-экономическая политика, войны и пр.). Одним из ключевых моментов системного подхода в демографии является выявление законов развития демографической системы, неизменных в течение длительного времени (даже в течение всего времени развития человечества) .
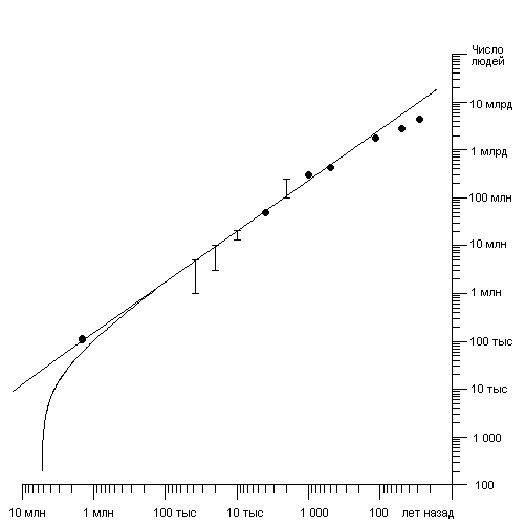
С.П.Капица в своих работах обобщил имеющиеся данные о численности народонаселения в различные исторические эпохи. Оказалось, в частности, что существующий режим роста населения Земли установился уже около миллиона лет назад, и, начиная с этого времени, рост полной численности человеческой популяции с хорошей точностью описывается гиперболическим законом N = C0/(Tf — T). (см. рис 1):
Рис. 1. Рост численности населения Земли. Гиперболический рост в двойном логарифмическом масштабе графика представляется прямой линией. Начальный участок кривой описывает выход системы на автомодельный асимптотический режим.
Момент обострения Tf, соответствующий обращению правой части формулы (1) в бесконечность, оказался неожиданно близким: это 2010-2020 год.
Этот фундаментальный факт вынуждает пересматривать привычное мировоззрение. Оказывается, что процессы бурного роста, такие как возрастание населения Земли, «экономическое чудо» или увеличение потока научной информации, происходят вовсе не по экспоненте. Экспоненциальный рост — это один из мифов классической науки. Большинство процессов лавинообразного роста происходят гораздо быстрее, в режиме с обострением, когда рассматриваемые величины хотя бы часть времени изменяются по закону неограниченного возрастания за конечное время.
Синергетическая модель роста народонаселения Земли, развивая системный подход к демографической системе, описывает человеческую популяцию как единую нелинейную открытую распределенную диссипативную систему. Динамика эволюции такой системы определяется, помимо необходимости выполнения закона роста полного числа людей (1), действием двух основных факторов.
С одной стороны, это — нелинейный источник, фактор, создающий и поддерживающий неоднородности в системе. В самом общем смысле — это действие нелинейных обратных связей, фактор самовлияния, самовоздействия, самоусиления процессов в демографической системе.
С другой стороны, это — диссипативный фактор, ослабляющий неоднородности в системе, своеобразный аналог диффузии. Это может быть миграция населения, распространение инфекционных болезней, передача знаний, научной и культурной информации, культурно-исторических традиций. Диссипативный фактор выражает общее влияние элементарных процессов на эволюцию макроскопических структур.
Синергетика позволяет снять некие психологические барьеры, страх перед сложными системами. Сверхсложная бесконечномерная система может описываться небольшим числом фундаментальных идей и образов, определяющих общие тенденции развертывания процессов в ней. На основании этого появляется возможность прогнозирования исходя: 1) «из целей» процессов (структур-аттракторов системы), 2) «от целого», исходя из общих тенденций развертывания процессов в сложных системах, и тем самым 3) из идеала, желаемого человеком и согласованного с собственными тенденциями развития процессов в данной системе. С практической точки зрения это означает, что появляется возможность описания эволюции сложных систем (и среди них демографической системы) с помощью достаточно простых математических задач.
3. Качественный анализ пространственной эволюции демографической системы.
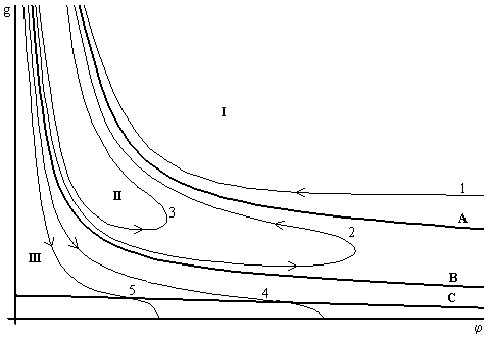
Для качественного анализа пространственной эволюции демографической системы в модели выделяются два параметра : j (характерный размер существующих в системе структур) и g (максимальная плотность населения в структуре расселения) (см. рис. 2).
На рисунке можно выделить три области: область гибели популяции III, область монотонного роста плотности населения (с монотонным уменьшением размера структур) I и промежуточная область II, в которой режим распространения и понижения плотности сменяется режимом роста и концентрации населения. Сепаратриса A является асимптотикой всех возрастающих решений. Она реализует режим с обострением и обеспечивает выполнение закона роста полного числа людей.
Рис. 2. Типичный вид фазовых траекторий g(j).
Решения, лежащие в области III, соответствуют широкому начальному распределению популяции с практически нулевой плотностью. Сепаратриса B соответствует неустойчивому равновесию существующих в естественных условиях популяций животных. Неустойчивость их, однако, имеет метастабильный характер, то есть при отклонении от равновесной кривой фазовая траектория долгое время остается близкой к ней, а затем резко удаляется (например, кривые 2 и 4). При большем отклонении от равновесия время метастабильности уменьшается (кривые 3 и 5).
Отклонение фазовой траектории от равновесной кривой B может происходить как в область формирования режима с обострением II, так и в область вымирания популяции III. Однако, повидимому, отклонения от нее в сторону роста являются более редкими, чам отклонения в сторону гибели популяции. Это связано, очевидно, с тем, что любая флюктуация оказывает с большей вероятностью отрицательное влияние на рост численности населения. Это происходит потому, что сепаратрисы B и C представляют собой локальные максимумы эффективности развития системы, и при небольших отклонениях от них эффективность развития (в том числе скорость роста численности населения) уменьшается.
Режим с обострением имеет такую особенность, что ход процессов в них имеет две существенно отличающиеся друг от друга стадии. Первая из них — это длительная метастабильная стадия, когда все характеристики процессов растут чрезвычайно медленно и незначительно. Все локальные флюктуации, возникающие на этом этапе, не меняют качественно хода эволюции системы, проявляясь лишь в небольшом изменении момента обострения. Все накопившиеся на этом этапе несогласованности в развитии различных частей системы проявляются на второй стадии — стадии асимптотической неустойчивости вблизи момента обострения, когда возникает угроза стохастического, «радиоактивного» распада любых сложных образований. Вблизи момента обострения сколь угодно малые локальные флюктуации способны рассогласовать темп развития внутри сложной структуры, в результате чего последняя подвергается реальной угрозе распада. Такой (стохастический, вероятностный) тип асимптотической неустойчивости сложных структур позволяет говорить о существовании в демографической системе особого типа странных аттракторов.
Траектория развития популяции человека до настоящего времени проходила полностью в области II. Начальный этап характеризовался быстрым распространением человека по территории Земного шара с медленным падением плотности населения в центре распространения. Далее (примерно 1 миллион лет назад) процессы в системе постепенно изменили свое направление. Начиная с этого времени население стало концентрироваться во все более узких структурах со все возрастающей плотностью вблизи центра концентрации.
Характер современной стадии развития человеческой цивилизации определяется во многом именно приближением демографической системы к «моменту обострения». Это — ускорение мировых процессов, возрастающая нестабильность, множество возможных, угрожающих миру глобальных опасностей (экологическая катастрофа, разгул терроризма, ядерный катаклизм). Важно понять, что проблема эволюционных кризисов носит общечеловеческий характер. Эволюционные кризисы и неустойчивость угрожают сегодня не только России, но и всему миру.
Асимптотическая неустойчивость сложных организаций, развивающихся в режиме с обострением, приводит к бифуркациям, к появлению нескольких возможных сценариев дальнейшего хода событий: гибели цивилизации, распада сложных структур, или «фазового перехода», выхода системы на новый режим развития. Что касается первого, пессимистического исхода, то это по сути глобальная версия известного исторического феномена — крушения империй. Крах Греческой и Римской империй, крушение кайзеровской Германии в 1918 г., после окончания первой мировой войны, распад колониальных систем Великобритании, Франции и Испании после второй мировой войны, распад СССР после периода холодной войны — все эти локальные катастрофы представляют собой, вероятно, проявления общей исторической закономерности краха империй. Как известно, историки не обсуждают вопроса, почему империи распадаются вообще, они исследуют только конкретные социальные причины и условия краха отдельных империй. Синергетические модели позволят, возможно, получить математическое обоснование этого исторического феномена.
Возможен ли другой путь, обратный переход с роста в режиме с обострением на режим распространения и уменьшения концентрации, «замыкание» фазовой траектории системы?
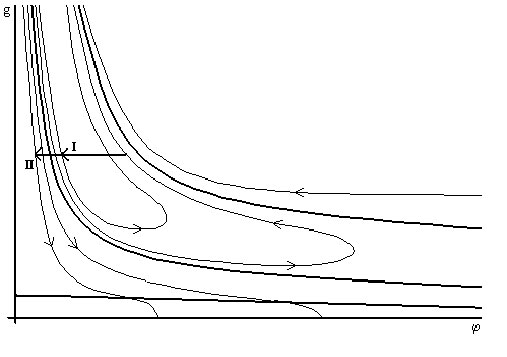
Да! Такую возможность предоставляют нам флюктуации, но не локальные, разрушающие синхронность процессов в различных регионах, а глобальные, влияющие на поведение системы в целом. Это например, — изменение глобальных параметров системы, характеризующих миграцию или скорость прироста населения. Было показано , что подобные флюктуации небольшой величины могут объяснить периодичность смены исторических эпох на протяжении всей истории развития человечества. Более существенные флюктуации могут стать причиной смены режима эволюции системы (см. рис. 3). Для поворота с режима роста на режим замедления и стабилизации населения, для выхода системы на новый аттрактор, нужны «потрясения» системы. Нужно пройти через слои хаоса, чтобы создать новую структуру, добыть новую информацию, иметь историческую инновацию вообще .
Рис. 3. Флюктуации, приводящие к смене режима развития демографической системы. Флюктуация I оставляет систему в области роста, флюктуация II переводит ее в область затухания и гибели популяции.
Например, усиление миграции населения приведет к эффективному уменьшению характерного размера структур и, при достаточной величине флюктуации, смене режима. В этом случае развитие человечество может принять экстенсивный характер, характеризующийся уменьшением максимальной плотности населения и существенно более медленным ростом полного числа людей. При этом характер развития будет определяться не только (и не столько) общей численностью народонаселения, сколько характером его пространственного распределения. Распространение и уменьшения концентрации населения ведет к симметризации системы, нивелируя рассогласованность различных регионов, накопившуюся в процессе роста в режиме с обострением. Такой путь развития, однако, содержит в себе новую опасность, приближая ее к термодинамическому равновесию, состоянию «тепловой смерти» — максимально простому состоянию системы. Тем не менее, существует некоторый отрезок времени, в течение которого структура системы будет сохраняться, в первую очередь благодаря нелинейности диссипативных процессов в системе. Таким образом, изменение параметров системы должно быть не слишком сильным (флюктуация I, а не II на рис. 3), а время экстенсивного развития системы не должно превышать времени метастабильной устойчивости существующих в системе структур.
Человечество являет собой счастливое исключение из общего правила о преимущественно отрицательном влиянии флюктуаций на развитие системы. Возможно, что перемещение человечества с характерной для большинства популяций метастабильной фазовой кривой B в область роста в режиме с обсотрением связан как раз с некоей глобальной флюктуацией, произошедшей около 1 млн. — 100 тыс. лет тому назад. Это была флюктуация, обратная стрелке II на рис. 3 (уменьшающая скорость распространения населения). Например, ею могло быть начавшееся около 150 тыс. лет назад оледенение.
Однако анализ роста полного числа людей показывает, что в дальнейшем отклонения от гиперболического автомодельного закона роста происходили преимущественно в сторону уменьшения численности народонаселения.
Динамика развития сложных социальных организаций и структур связана, таким образом, с периодическим чередованием режимов убыстрения процессов и их замедления, режимов кристаллизации и стирания различий, частичного распада структур, с периодическим смещением фокуса влияния от центра к периферии и обратно. Попятное движение по времени, частичный возврат к старому, к культурным и историческим традициям является, вероятно, необходимым условием поддержания сложной социальной организации.
4. Демографические аспекты рассматриваемой модели.
Что же дает современным демографам, социологам, футурологам синергетический подход в целом и, в частности, предложенная модель? Прежде всего — неединственность, существование спектра аттракторов системы приводит к тому, что даже две абсолютно одинаковые системы, стартовавшие с разных начальных позиций, могут иметь совершенно различные пути эволюции. Это означает, что не всегда можно использовать для управления или прогнозирования опыт развития других стран или предшествующих эпох. Разные начальные данные и внешние условия могут привести к принципиально иному сценарию развития, чем ожидается.
Далее — понятие о когерентности. Рассмотрение сложных структур в двух- и трехмерном случаях, проведенные в ИПМ им. М.В.Келдыша РАН , показали, что различные регионы сложной структуры могут не иметь одинакового уровня развития. Критерием устойчивости сложной структуры является согласованность темпов роста в различных ее частях (общий для всей сложной структуры момент обострения). В противном случае сложная структура быстро вырождается или распадается на простые. Это означает также, что по мере приближения к моменту обострения различия в уровень развития частей сложной структуры становятся сколь угодно велики, однако отставание в развитии по времени у менее развитых областей становится все меньшим.
Асимптотический характер развития демографической системы в течение миллиона лет (рис. 1) означает, что для анализа можно было использовать результаты многолетних исследований законов эволюции подобных систем, проведенных в Институте Прикладной Математики им. М.В.Келдыша РАН. Методом ПАР (приближенных автомодельных решений) было строго доказано, что асимптотическая стадия эволюционных процессов в ней, т.е. структуры-аттракторы демографической системы, описывается инвариантно-групповыми решениями .
Инвариантно-групповая асимптотика модельных уравнений выражается в формировании на асимптотической стадии связи между пространственной и временной координатами. Поскольку в инвариантно-групповых решениях пространство и время не свободны, а определенным образом связаны друг с другом, необходимо перейти к пространственно-временному описанию эволюционных процессов. Анализ глобальной демографической системы показал существование в ней пространственно-временных инвариантов, подобных инвариантам Специальной Теории Относительности. В данном случае, в отличие от СТО, инвариантным является не аддитивное выражение (интервал s2 = c2t2 — x2 — y2 — z2), а выражение отношения (x = x / j(t)).
На рис. 1 мы видно, что человечество уже давно (около миллиона лет назад) вышло на асимптотическую стадию развития. Это означает, что существует принципиальное соответствие между законами эволюции развитых регионов мира сегодня и удаленных от центра цивилизации регионов Земли в прошлом. Более того, зная законы развития автомодельного решения на «хвосте» структуры (это могут быть географически удаленные регионы мира — Австралия, Америка, возможно, Япония, или отсталые в социально-экономическом отношении страны; это также могут быть наименее заселенные районы в различных странах) в настоящий момент, можно было бы предсказать качественное поведение системы вплоть до момента обострения, однакосуществуют принципиальные ограничения возможности прогнозирования (строгая локализация решения при локализованной начальной функции), формирующие «горизонт предсказуемого будущего». Следовательно, прогнозы, основанные на существовании некоторых «инвариантов эволюции», получаемых эмпирическим образом из анализа существующих и прошлых тенденций эволюции, не могут быть построены на любой наперед заданный срок.
Режим с обострением приводит к возникновению центров кристаллизации, сгущения населения — поселков и городов, регионов с высокой концентрацией населения. В условиях конкуренции факторов нелинейного самовлияния и диффузии равномерное распределение населения неустойчиво. Возникают центры концентрации населения, многополюсная и разноуровневая структура расселения. Формирование такой структуры носит квантовый характер. Это означает, что не любая конфигурация системы может сформироваться или сохраняться в течение длительного времени, даже при существенных затратах, направленных на ее поддержание.
Существуют выделенные состояния (структуры-аттракторы), к которым направлено развитие системы, а все остальные состояния неизбежно эволюционируют к одному из аттракторов. Аттрактор — это нестационарная динамическая диссипативная структура, эволюционирующая в соответствии с инвариантно-групповыми закономерностями, характерными для системы . Выделенность структур-аттракторов среди прочих состояний системы определяется в первую очередь когерентностью развития системы в этом состоянии. Критерием устойчивости демографической структуры является не одинаковый уровень развития, а согласованность темпов роста, принадлежность к единому темпомиру. В противном случае несогласованные нелинейные процессы быстро разрушат организацию, структура распадется или выродится. Более того, по мере приближения к моменту обострения различие в уровне развития отдельных стран и регионов должно увеличиваться, однако отставание в развитие по времени у менее развитых областей становится все меньшим, что и наблюдается в настоящее время.
Структуры-аттракторы представляют собой, по существу, цели развития системы. Одной их основных проблем в рамках синергетическиго подхода является поиск таких целей, «конечных причин» эволюции системы, тогда как классический подход подразумевал исследование «действующих причин», механизмов отдельных явлений, происходящих в системе. Эволюция системы происходит так, как если бы путь развития определялся тем состоянием, в которое система должна прийти. Это кажущееся нарушение принципа причинности объясняется тем, что существует множество путей, приводящих систему к этому состоянию, а также устойчивостью самой структуры-аттрактора.
Исследование структур-аттракторов системы важно еще и потому, что оно дает представление о сложности организации системы. Сложно-организованная система должна иметь большое число различных структур-аттракторов. Так, например, имеется около сотни видов атомов, лежащих в основе всей нашей Вселенной. Количество белков, участвующих в построении биологических объектов, составляет десятки и сотни тысяч, а число различных видов клеток, существующих или когда-либо существовавших, исчисляется миллионами.
Известна формулировка антропного принципа, связанного с происхождением Вселенной. Сложность наблюдаемой Вселенной определяется очень узким диапазоном вероятностей первичных элементарных процессов и значений фундаментальных констант. Если бы вероятности элементарных процессов в эпоху Большого взрыва были, скажем, немного выше, то вся Вселенная «выгорела» бы за короткий промежуток времени. Антропный принцип оказывается принципом существования сложного в этом мире. Чтобы на макроуровне сегодня было возможно существование сложных систем, элементарные процессы на микроуровне изначально должны были протекать очень избирательно.
Возможно распространить антропный принцип на условия проявления «сложности» в явлениях самоорганизации. Дело в том, что (как показали строгие математические расчеты и численные эксперименты, проведенные в ИПМ РАН и в МГУ) сложный спектр квазиустойчивых динамических структур, отличающихся различными размерами и формами, существует лишь для узкого, уникального («антропного») класса моделей . В этих моделях асимптотическая стадия эволюции системы описывается уравнениями со степенными нелинейными зависимостями.
Неудивительно, что именно степенная зависимость имеется в автомодельном законе роста численности населения Земли.
Синергетическая модель демографической системы, построенная с учетом пространственного распределения населения, позволила описать ряд парадоксальных фактов, подтверждающих необходимость рассмотрения человечества как единой системы не только в Новое время, но практически с момента формирования человека как биологического вида: это удивительная устойчивость гиперболического закона роста в течение сотен тысяч лет, синхронность смен исторических эпох в различных регионах Земного шара. Кроме того, модель обосновала указанную С.П.Капицей периодичность в смене исторических эпох и тот факт, что относительная скорость роста населения оказалась пропорциональной удалению в прошлое от современности (на самом деле от момента обострения) .
Для устойчивого развития система должна иметь возможности перехода в критические моменты с интенсивного роста в режиме с обострением на экстенсивный режим распространения и обратно, образуя таким образом полный цикл эволюции. Механизмом такого перехода могут быть, например, дополнительные, несущественные до этого, источники и стоки в уравнении (1.1) или изменение коэффициентов C и Q этого уравнения, которые обеспечили бы синхронный переход системы на другую фазовую кривую, в отличие от точечных флюктуаций, которые, нарушая единый для структуры темп развития, как правило, разрушают ее.
Предполагаемые аналоги такого циклического изменения тенденция развития можно видеть в эволюции многих сложных систем, начиная с биоритмов и заканчивая расширением и сжатием Вселенной.
5. Литература
1. Ахромеева Т.С., Курдюмов С.П., Малинецкий Г.Г., Самарский А.А. Нестационарные диссипативные структуры и диффузионный хаос. М.: Наука, 1992.
2. Белавин В.А. Квазилинейное уравнение теплопроводности с источником. Метод осреднения и автомодельность. //Препринт ИПМ АН СССР № 51, 1998.
3. Белавин В.А., Капица С.П., Курдюмов С.П. Математическая модель демографических процессов с учетом пространственного распределения. //Ж.вычисл. матем и матем. физ. 1998. Т.38. №6. С.885-902
4. Белавин В.А., Курдюмов С.П. Режимы с обострением в демографической системе. Сценарий усиления нелинейности. //Ж.вычисл. матем и матем. физ. 2000. Т.40. №2. В печати.
5. Belavin V.A., Knyazeva E.N., Kurdyumov S.P.. Blow-up and laws of co-evolution of complex systems. // Phystech Journal, 1997, vol. 3, № 1, pp.107-113.
6. Вишневский А.Г. Воспроизводство населения и общество, М.: Финансы и статистика, 1982.
7. Еленин Г.Г., Курдюмов С.П.. Условия усложнения организации нелинейной диссипативной среды. Препринт № 106 ИПМатем. АН СССР, 1977.
8. Еленин Г.Г., Плохотников К.Э.. Об одном способе качественного исследования одномерного квазилинейного уравнения теплопроводности с нелинейным источником тепла. //Препринт ИПМ АН СССР № 91, 1977.
9. Капица С.П. Феноменологическая теория роста населения Земли. //Успехи физ. Наук, 1996, т. 166, № 1, с.63-79.
10. Капица С.П. Математическая модель роста народонаселения Земли. //Матем. Моделирование. 1992. Т.4. № 6. С.65-79;
11. Капица С.П., Курдюмов С.П., Малинецкий Г.Г. Синергетика и прогнозы будущего. М., Наука, 1997.
12. Князева Е.Н., Курдюмов С.П.. Антропный принцип в синергетике. //Вопр. философии, 1997, № 3, с.62-79.
13. Князева Е.Н., Курдюмов С.П. Законы эволюции и самоорганизации сложных систем. М.: Наука, 1994. 236 с.
14. Князева Е.Н., Курдюмов С.П.. Синергетика как новое мировоззрение. Диалог с И.Пригожиным. //Вопр. философии, 1992, № 12, с.3-20.
15. Князева Е.Н., Курдюмов С.П. Синергетика в контексте диалога Восток — Запад // Россия и современный мир. М.: ИНИОН РАН, 1995. N 3.
16. Князева Е.Н., Курдюмов С.П. Синергетика и Восток: близость далекого // Духовные истоки Японии. Альманах./ Под ред.Т.П.Григорьевой. М.: Толк, 1995.
17. Курдюмов С.П., Куркина Е.С., Потапов А.Б., Самарский А.А.. Сложные многомерные структуры горения нелинейной среды. //Ж.вычисл. матем. и матем.физ., 1986, т.26, № 8.
18. Kurdyumov S.P., Malinetskii G.G., Potapov A.B. Nonstationary Structures, Dynamic Chaos, Cellular Automata. //Intern. Journ. of Fluid Mech. Research. V.22. №5-6. P.75-133.
19. Kurdyumov S.P.. Evolution and self-organization laws in complex systems. //International Journal for Modern Physics, C, 1990, v.1, № 4, pp.299-327.
20. Николис Г., Пригожин И.. Познание сложного. М.: Наука, 1990.
21. Наука, техника, вычислительный эксперимент. Сб. статей. М., Наука, 1993.
22. Самарский А.А., Галактионов В.А., Курдюмов С.П., Михайлов А.П.. Режимы с обострением в задачах для квазилинейных параболических уравнений. М.: Наука, 1987.
23. Хаген Г.. Информация и самоорганизация. Макроскопический подход к сложным системам. М.: Мир, 1991.