Синергетику определяют по-разному. Одно из последних и удачных определений принадлежит Ю.Л.Климонтовичу: «Синергетика — не самостоятельная научная дисциплина, но новое междисциплинарное научное направление; цель синергетики — выявление общих идей, общих методов и общих закономерностей в самых разных областях естествознания, а также социологии и даже лингвистики; более того в рамках синергетики происходит кооперирование различных специальных дисциплин

Доктор Р.Фейнман в непревзойденных лекциях по физике воспел иерархическое дерево познания, на корнях и ветвях которого разрослись разнообразные разновзглядовые, разноподходовые культуры. Спрашивается — возможно ли в принципе нам — людям — охватить целиком («широкоугольно») все на свете, включая нас самих…
М.А. Миллер

Каждый человек, особенно в детстве, хочет понять окружающий мир, а позднее свое место в нем. Увы, как показывают исследования, школа часто отбивает охоту познавать мир. Известный русский мыслитель Д.И.Писарев в работе «Наша университетская наука» еще в 1863 году писал, что система образования того времени отличалась следующим: «…различные предметы не связываются в общий цикл знаний, не поддерживают друг друга, а стоят каждый сам по себе, стараясь вытеснить своего соседа… Каждый предмет бывает то победителем, то побежденным; история их постоянных раздоров составляет историю умственной жизни каждого гимназиста; мозг ученика — вечное поле сражения, а пора экзаменов — время самых истребительных войн между отдельными предметами».

Прошло более ста лет, но ситуация в целом мало в чем изменилась и в средней, и в высшей школе. Несмотря на привычную приговорку о междисциплинарных связях, чаще всего изучение отдельных предметов никак не уживается друг с другом. Откуда тогда взяться тому, что называется картиной мира? Да, и одна ли она? Пожалуй, можно говорить, по крайней мере, о трех таких полотнах, написанных учеными-художниками разных стилей: естественнонаучной картине мира, социальной картине мира и религиозной. Но, если первая, как правило, не зависит от того, в какой стране вы живете, то две других зависят от этого.

Впрочем, они зависят часто и друг от друга. В нашей стране вместе со старым порядком рухнула старая социальная картина мира. Как пишет А.С.Панарин в статье «Политология на рубеже культур», подобное крушение «… означает разрыв с той лапласовской вселенной, в которой до последнего времени пребывала наша социальная философия». Любопытны и его дальнейшие рассуждения. «В самом деле, если существуют непреложные исторические закономерности, предопределяющие ход истории в заранее заданном (к коммунизму) направлении, то, что же остается на долю политики? Выполнять предначертания «исторического разума».

Если история — эскалатор, который вывезет наверх, в светлое будущее, то в политике нет реального выбора и реального риска. Все ее противостояния основаны на недоразумении, на незнании или злостном сопротивлении «реакционных классов» логике единственно возможного. Политическая борьба есть, таким образом, не более чем лицедейство истории, которое ее высший разум почему-то терпит до поры до времени, хотя победители ему изначально известны. Естествознание давно уже покончило с этими лапласовскими представлениями, открыв сложность, нелинейность, неопределенность. Соответствующий переворот в социальной картине мира у нас заставил себя ждать до последнего времени.» Та часть естествознания, которая покончила с лапласовскими представлениями, выделилась в самостоятельной междисциплинарное направление — синергетику (или нелинейную динамику), претендующее на новое научное мировоззрение. Поиск общего в разном — вот смысл этого мировоззрения, а ключевыми понятиями являются колебания и волны, неустойчивость и нелинейность, хаос и структуры.

Синергетику определяют по-разному. Одно из последних и удачных определений принадлежит Ю.Л.Климонтовичу: «Синергетика — не самостоятельная научная дисциплина, но новое междисциплинарное научное направление; цель синергетики — выявление общих идей, общих методов и общих закономерностей в самых разных областях естествознания, а также социологии и даже лингвистики; более того в рамках синергетики происходит кооперирование различных специальных дисциплин»[1]. Уже из определения следует, что синергетика вполне может претендовать на роль подходящего инструмента для решения двух важных проблем сегодняшнего образования:

1. проблемы плавного перехода среднего образования в высшее и
2. проблемы постепенного создания в мыслях каждого молодого человека картины современного окружающего мира .

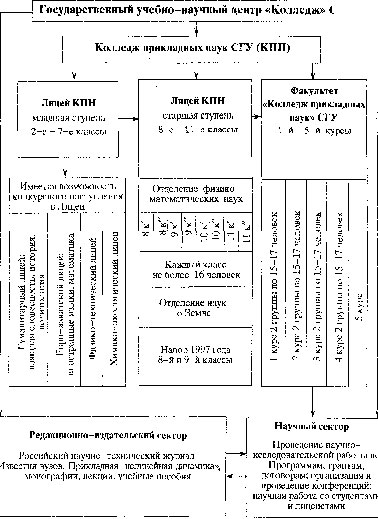
В Саратовском государственном университете в 1992 году была создана новая учебная структура — Колледж прикладных наук (КПП), имеющая статус факультета и входящая в состав Государственного учебно-научного центра «Колледж» (ГосУНЦ «Колледж»). Учебный процесс в КПП построен на идеях синергетики. Структура ГосУНЦ и КПН представлена на схеме . КПН существую пять лет. За это время было два выпуска Лицея КПН (ЛКПН). На университетском факультете четыре курса. Несоответствие числа выпусков курсов объясняется тем, что два курса были набраны по конкурсу из абитуриентов города и области. Цель — как можно

Заметим, что неологизм «синергетика», введенный в обиход немецким физиком Германом Хакеном, происходит от греческого «синергиа» — сотрудничество, содружество. Хакен подчеркивал, что этот термин акцентирует внимание на согласованности взаимодействия частей при образовании структуры как единого целого. Если вспомнить, что латинское universitas — объединение, то легко понять, что синергетический подход буквально создан для университета.
В статье речь пойдет о физико-математическом отделении ЛКПН, поскольку отделение наук о Земле создано лишь в этом году.

раньше начать отработку университетских курсов в синергетическом ключе. Конечно, здесь были трудности, поскольку поступившие не прошли «школьную синергетику», и многому пришлось учить заново.
Одна из основных целей КПН — создание атмосферы творчества и духовной свободы детей, начиная с младшей ступени ЛКПН. На этой ступени, конечно, никакой предопределенности в выборе дальнейшего направления учебы нет: совсем не обязательно идти на старшую ступень ЛКПН, можно на конкурсной основе поступать в другие университетские лицеи (см. схему), в другие городские учебные заведения. На этой ступени просто хорошо учат, и это главное.

После окончания младшей ступени лицеист, решивший продолжить учебу на старшей ступени ЛКПН, или абитуриент-семиклассник из другой общеобразовательной школы обязаны сдавать вступительные экзамены в трех турах. Первый тур — домашний. Газета «Саратовский университет» печатает задания по математике и физике (задания достаточно трудны, выполнение их требует фантазии выхода за рамки скромных знаний по физике ученика седьмого класса). На этом этапе отсеиваются те, кто либо случайно участвует в конкурсе, либо переоценил свои возможности, либо пошел за компанию вместе с другими.

Желающих на этом этапе много: рекордная цифра однажды была 700 человек на 32 места. Однако ко второму туру, состоящему из двух письменных экзаменов — по математике и физике — остается человек 200-250. Практически мы допускаем ко второму туру всех, выполнивших домашнее задание. Особенность экзамена по физике в том, что в него входит сочинение по физике, которое проверяют преподаватели физики и литературы. Из тем сочинений прошлых лет у детей пользовались популярностью следующие: «Пропало трение. Что будешь кричать: «Ура!» или «Караул!»?»; «Я — молекула»; «Отчего деревья не растут до неба?». Кстати, на последнем уроке этого года в 11-ом классе ответ на последний вопрос был дан уже с высоты знаний оканчивающего старшую ступень ЛКПН. На вступительных экзаменах в мае 1997 года восьмиклассникам были предложены темы: «Физические законы в русских народных сказках»; «Простые механизмы в старинных войнах»; «Я — Архимед, а он — Паскаль»; «Взаимодействия бывают разные — в физике весьма разнообразные». Кроме того были даны две задачи на выбор (кроме двух стандартных): 1. Оцените выталкивающую силу, действующую на человека со стороны воздуха в комнате; 2. Оцените скорость воздуха, с которой можно выдувать его ртом через трубку. Наконец, третий тур — собеседование, на котором надо отобрать всего 32 человека . На собеседовании речь идет обо всем — и о математике, и о физике, и о литературе; проверяется уровень знаний иностранного языка.
На старшей ступени ЛКПН все дисциплины можно условно разбить на четыре цикла.

• Цикл 1. Математика, физика, информатика, включая спецкурсы «Аналитическая геометрия», «Как решать задачи по физике», «Математические методы естествознания». В настоящее время два последних спецкурса естественным образом «размещены» в соответствующих местах курса физики.
• Цикл 2. Естественные науки (биология с экологией, география, химия).
• Цикл 3. Гуманитарные науки (русский язык и литература, история, человек и общество), включая специальные курсы русской и мировой поэзии, изобразительного искусства, музыки, театра и двух иностранных языков (английский и немецкий) .
• Цикл 4. Колебания, волны, синергетика (с экзаменом в 11-ом классе, включающим доклад на избранную тему).

Последний цикл является ключевым для реализации синергетического подхода при построении современной картины мира, поэтому остановимся подробно на его программе. В 9-ом классе курс длится лишь одно полугодие (второе) и включает лекции, семинары по решению задач и выполнению курсовой работы. Лекционную часть курса составляют следующие разделы (именно в таком виде они выносятся в программу заключительного экзамена в 11-ом классе) .

9 класс

Раздел 1. Основные положения теории размерностей и подобия (определение размерности физической величины; выражение размерности физической величины через размерности, принятые за основные; подобие физических систем).
Определение математического маятника с помощью анализа размерностей.
Дополнение Хантли (пример: зависимость длины свободного пробега молекулы от размера молекул и их концентрации).
Раздел 2. П-теорема. Определение периода колебаний цефеид.
Раздел 3. Линейный осциллятор — основная модель линейной теории колебаний.
Вывод уравнения гармонического осциллятора на примере маятника. Груз на пружине с учетом трения — пример линейного осциллятора.
Раздел 4. Химический, экологический и экономический осцилляторы.
Параллельно с лекциями решается большое число задач, что позволяет учащимся к концу полугодия свободно владеть анализом размерностей, некоторыми методами оценок и понять общность модели линейного осциллятора. Каждый из учащихся ЛКПН выполняет в этом полугодии и курсовую работу на одну из следующих тем.
o Анализ размерностей и задачи кинематики.
o Анализ размерностей в задачах астрофизики.
o Анализ размерностей и «маятники» разной природы.
o Анализ размерностей и задачи гидродинамики.
o Дополнение Хантли и его использование в задачах кинематики.
o Математический маятник, U-образная трубка, вертикально плавающий в жидкости цилиндр, цефеиды — это просто разные маятники (доказательство с точки зрения анализа размерностей).
o Анализ размерностей и задачи о вязкой жидкости.
o О подобии физических систем (критерии подобия на примере конкретных задач).
o Анализ размерностей и разные задачи о колебаниях.
o Анализ размерностей и задачи механики.
В качестве дополнительной к лекциям литературы лицеистами используются книги [1-6]. Лучшие работы докладываются на студенческой конференции физического факультета СГУ на секции первокурсников.
Программы лекционных частей курса в 10-ом и 11-ом классах приведем целиком.

10 класс

1. Синергетика — новый взгляд на мир. Хаос и структуры (вводный очерк). О содержании второй части курса.
2. Математическое отступление. Интеграл. Определение пути по скорости движения и площадь под кривой. Связь между интегралом и производной. Интеграл от производной. Неопределенный интеграл. Свойства интегралов. Средние значения. Простейшие интегралы.
3. Что такое динамическая система? Понятие о фазовом пространстве. Фазовый потрет гармонического осциллятора. Линейная система с отталкивающей силой.
4. Математическое отступление. Комплексные числа. Основные свойства комплексных чисел. Сопряженные комплексные числа. Тригонометрическая форма комплексного числа. Возведение в мнимую степень. Формулы Эйлера и Муавра. Логарифмы и корни.
5. Описание гармонических колебаний с помощью показательной функции мнимого аргумента. Электрический контур.

6. Гармонический осциллятор с сухим трением. Гармонический осциллятор с линейным трением. Обобщение на осцилляторы любой природы. Карта фазовых портретов «обобщенного» осциллятора. Квантовый осциллятор.
7. Математические модели в синергетике. Динамическая система — основная модель синергетики. Плоский маятник. Игра «Жизнь».
8. Резонанс. Резонанс в гармоническом осцилляторе. Аналитическое решение, демонстрирующее не неограниченный рост амплитуды под действием гармонической силы. Влияние затухания на резонанс. Примеры резонанса: солдаты шагают по мосту; резонатор Гельмгольца и … домовой, колдун, глиняные или бронзовые сосуды в античном театре; тяжелый колокол; «поющий камень»; осциллятор атмосфера Земли и другие глобальные резонансы; клистрон — стодолларовая идея братьев Вариан.
9. Линейные волны. Оценки для гравитационных и капиллярных волн на основе анализа размерностей.
10. Голубое небо и Нобелевская премия по физике за 1930 год (от Леонарда Эйлера к Рэлею, Мандельштаму, Смолуховскому, Эйнштейну, вновь к Мандельштаму, Раману и к современной теории рассеяния).
11. Неустойчивость в системах различной природы. Струна, нагруженная одинаковыми телами, расположенными на одинаковом расстоянии друг от друга. Волновое уравнение. Пространственный резонанс (примеры — сверхвысокочастотные лампы бегущей и обратной волны).
Литература к программе представлена в ссылках [5,7-9].
Третья часть курса состоит из двух больших разделов.

11 класс

Раздел 1. Нелинейные колебания и волны. Хаос и образование структур.

1.1. Синергетика (нелинейная динамика) и образование XXI века. Экология и синергетика. Цивилизация потребления, экологический кризис и исходы из него. О неолитическом кризисе. Каким должен быть новый кризис? Какое образование нужно для выхода из него? Разрушение стереотипов в нелинейной динамике. Некоторые положения нелинейной динамики, важные для стратегии перехода к новой цивилизации. Социально-экономические дисциплины и синергетика. Синергетика искусства? Может быть… О чем третья часть курса.

1.2. Нелинейные колебания. Колебания в консервативных системах. Начнем с воспоминаний: гармонический осциллятор; фазовая плоскость и фазовый портрет гармонического осциллятора. Отталкивающий гармонический потенциал. Нелинейный осциллятор — основная модель нелинейной теории колебаний. Частица в ящике. Потенциал U(x)=th2x (яма конечной глубины). Фазовый портрет одномерного движения. Солдаты опять идут по мосту — фазовая группировка нелинейных осцилляторов. Мазеры и гиротрон. Нелинейный маятник — модель в теории лазера на свободных электронах. Неконсервативные колебания. Гармонический осциллятор с сухим трением. Гармонический осциллятор с линейным трением. Карта фазовых портретов обобщенного осциллятора . Движение под действием потенциальной силы при наличии линейного трения.

1.3. Автоколебания. Общие свойства автоколебательных систем. Гюйгенс и часы. Автоколебания в часовом механизме. Ламповый генератор. Стационарное состояние и условие возникновения колебаний. Параметры колебаний при ступенчатой характеристике лампы. Предельные циклы и их свойства. Пуанкаре, Ван-дер-Поль, Мандельштам, Андронов и их роль в теории автоколебаний. Магнетрон спасает Великобританию от гитлеровской авиации (по Чарльзу Сноу).

1.4. Нелинейные волны. Поток невзаимодействующих частиц и нелинейные волны. Что такое простая волна? Опрокидывание волны на спектральном языке. Ударные волны. Землетрясение — сильный точечный подземный взрыв (опять анализ размерностей). Проблема Ферми — Паста — Улама и солитон. Скотт Рассел: «… потерял его в извилинах канала». Почему возможен солитон (объяснение на спектральном языке). Как получать уравнения нелинейных волн феноменологически? Уравнение Кортевега — де Вриза. Нелинейный осциллятор и солитон. Солитоны в физике и биологии.

1.5. О хаосе и об образовании структур. «Хаос больше не бранное слово!» (немного истории от Пуанкаре до Эдварда Лоренца и др.) Как возникает случайность в динамической системе. Детерминированный хаос. Странный аттрактор. Алгоритмическое объяснение хаоса. А все началось с модели Лоренца. Турбулентность и переход к хаосу по сценарию Фейгенбаума. К хаосу ведет много путей (о разных сценариях возникновения хаоса в динамических системах). Фракталы и их связь с детерминированным хаосом. Самоорганизация и образование структур. Классификация структур. Структуры Тьюринга и проблемы морфогенеза. Ячейки Бенара. Автоструктуры. Автоволны: пожар тушат пожаром; «Свеча горела на столе, свеча горела»; бегущий фронт; ведущий центр ревербератор и др.

1.6. Сложность (о связи хаоса и структур).
Литература к этой части курса представлена в ссылках [5, 10].
Раздел 2. Как идеи нелинейной динамики проникают в экологию, экономику, социальные науки и медицину
2.1. Модели развития и взаимодействия в экологии (модель Мальтуса и ее обобщение Ферхюльстом, модель Вольтерра — Лотки). Детерминированный хаос в модели «хищник — жертва — пища».
2.2. Странный феномен логистического уравнения. Не слишком ли много оно описывает (эволюция популяции в экологии, эволюция научной продукции, деятельность «Красных бригад» в Италии, развитие готического стиля в архитектуре и др.)
2.3. Современные модели народонаселения.
2.4. Нелинейные модели в экономике и социальных науках. Циклы Кондратьева в экономике. Модели Гудвина цикла капиталистической экономики.
2.5. Математическая модель Ю.И.Неймарка сосуществования производителей и управленцев.
2.6. Нелинейные модели Вольфганга Вайдлиха и их применение к экономическим и социальным задачам (взаимодействие народа и правительства, перестройка по Горбачеву, взаимодействие старой и новой отраслей промышленности, эволюция модного ресторана).
2.7. Хаос и структуры в социально-экономических моделях (развитие системы образования в условиях конкуренции, формирование общественного мнения, эволюционирующий рынок).
2.8. Динамические болезни. Общее понятие о динамических болезнях. Гольдбергер и др.: «Остановка сердца представляет собой бифуркацию от фрактальной, хаотической динамики нормальных сердцебиений к патологическим ритмам умирающего сердца». Так ли это? Какой должна быть терапия, если хаос — норма?
Литература к этой части курса представлена в ссылках [11,12].

Как уже указывалось, параллельно с чтением курса проводятся семинарские занятия по решению задач (главным образом по первой и второй частям курса). В начале учебного года в 11-ом классе предлагаются темы докладов для публичного выступления на заключительном экзамене. В качестве отправной точки для доклада рекомендуются статьи из журналов «В мире науки» и «Природа». Среди выбираемых тем выделим следующие.

• Самоорганизованная критичность (ВМН, 1991, N 3, с. 16-24).
• Перемешивание жидкостей. Струи, вихри, турбулентность (ВМН, 1988, N 3, с. 34-44; Природа, 1989, N 11, с. 33-37).
• Фрактальный рост (ВМН, 1985, N 3, с. 36-45).
• Компьютер в роли музыкального инструмента (ВМН, 1987. N 4, с. 72-80).
• Физические процессы в органных трубах (ВМН, 1983, N 3, с. 60-70). Звуки мышц (ВМН, 1984, N 5, с. 62-69).
• Отчего у леопарда пятна на шкуре (ВМН, 1988, N5, с. 46-54).
• Физики задумываются над механизмом работы мозга (Природа, 1987, N 3, с. 15-26) и др.

С выходом Соросовского журнала появилась возможность «освежить» тематику докладов. Разумеется, выбранная статья лишь определяет контуры доклада, потому требуется использовать много дополнительной литературы и консультироваться с преподавателем.

Выше подробно описан синергетический курс. Однако важно, что идеи синергетики вводятся и другие курсы. В курсе информатики предлагаются задачи нелинейной динамики, которые требуют использования компьютера. В частности, лицеисты в процессе занятий понимают, что открытие детерминированного хаоса и развитие фрактальной геометрии стали возможны только благодаря компьютерам. Поучительным для них является, например, повторение пути Митчела Фейгенбаума, когда он открыл сценарий возникновения хаоса, названный впоследствии его именем, исследуя отображение где l лежит в интервале 0 Ј l Ј 4.

• На занятиях по английскому языку лицеистам предлагаются для перевода простые статьи по нелинейной динамике из соответствующих научно-популярных и научных журналов.
• На уроках химии они экспериментально изучают периодические химические реакции.
• В новом учебном году предполагается введение спецкурса по дискретной математике, где определенное место отводится последовательному изучению отображений.
• На уроках биологии рассматриваются процессы взаимодействия хищников и жертв, проблемы морфогенеза и некоторые аспекты самоорганизации.

Пока лишь на уровне обсуждения находится введение синергетических идей в преподавание географии (хотя очевидно, что здесь они естественно входят, например, в разделы, связанные с погодой на Земном шаре и океаническими волнами, с образованием и разрушением гор, с землетрясениями и т.п.) и в гуманитарные дисциплины. Правда, в последнем случае делаются попытки обращения к работам [13-15], с идеями которых далеко не во всем можно согласиться. Поэтому речь идет скорее о критическом обсуждении той или иной идеи.

Выпускные экзамены в ЛКПН проводятся преподавателями лицея совместно с соответствующими приемными комиссиями СГУ и являются одновременно вступительными на университетскую ступень КПН. Сдаются следующие экзамены как вступительные: математика (письменно и устно), русский язык и литература (сочинение), физика (устно), английский язык (устно). Кроме того, учитывается результат экзамена по курсу «Колебания, волны, синергетика». Поскольку у ЛКПН нет интерната, с этого года открыто заочное отделение, которое позволит школьникам области и других городов России поступать на университетскую ступень КПН.

Следует подчеркнуть еще раз, что отличительная черта КПН в том, что он вписан в структуру университета как факультет. Окончившие ЛКПН не «растворяются» в разных факультетах СГУ, а продолжают учебу двумя группами, перешедшими из ЛКПН. Лишь единицы окончивших лицей выбирают другие ВУЗы. Из выпускников 1997 года один поступил в знаменитый Физтех без экзаменов как победитель зональной республиканской олимпиады по физике, еще двое — в не менее знаменитую Бауманку, несколько человек поступили в другие вузы Саратова.

Литература

1. Климонтович Ю.Л. Ввведение в физику открытых систем \\ Соросовский образовательный журнал. 1996. №8. С.111.
2. Коган Б.Ю. Размерность физической величины. М.: Наука, 1968.
3. Седов Л.И. Методы подобия и размерности в механике. М.: Наука, 1977.
4. Хантли г. Анализ размерностей. Пер. с англ. М.: Мир, 1970.
5. Трубецков Д.И. Колебания, волны, электроны. Саратов: ГосУНЦ «Колледж», 1993.
6. Дибай Э.А., Каплан С.А. Размерности и подобие астрофизических величин. М.: Наука, 1976.
7. Зельдович Я.Б. Высшая математика для начинающих и ее приложения к физике. М.: Наука, 1960.
8. Фадеев Д.К., Никулин М.С., Соколовский И.Ф. Элементы высшей математики для школьников. М.: Наука, 1987. Гл. 7.
9. Зельдович Я.Б., Мышкис А.Д. Элементы прикладной математики. М.: Наука, 1972. Гл.V. С. 144-163.
10. Неймарк Ю.И. Математические модели естествознания и техники. Цикл лекций. Вып.2. Нижний Новгород: Изд-во Нижегород. ун-та, 1996.
11. Неймарк Ю.И. Математические модели естествознания и техники. Цикл лекций. Вып. 1. Нижний Новгород: Изд-во Нижегород. ун-та, 1994.
12. Короновский А.А., Трубецков Д.И. Нелинейная динамика в действии. Как идеи нелинейной динамики проникают в экологию, экономику и социальные науки. Саратов: Изд-во ГосУНЦ «Колледж», 1995.
13. Евин И.А. Синергетика искусства. М., 1993.
14. Коваленко В.В. Бифуркации в религиозной философии, естествознании и общественном развитии. СПб.: Гидрометеоиздат, 1994.
15. Ласло Эрвин. Век бифуркации. Постижение изменяющегося мира // Путь. 1995. № 7. С. 3-129.