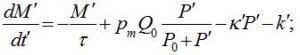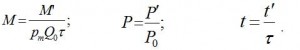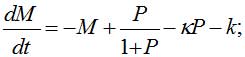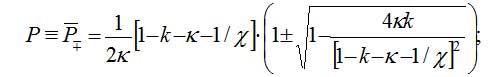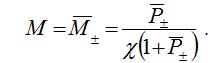ВВЕДЕНИЕ.

В моделях микроэкономики обычно предполагается, что предприятие работает непрерывно. При этом износ оборудования, конечно, имеет место. Но текущий ремонт и замена оборудования происходят постепенно, не прерывая режим работы. В работах [1] было замечено, что реально замена оборудования на новое (и более совершенное, т.е. реконструкция) в непрерывном режиме невозможна. Была сформулирована концепция периодической работы предприятия

Суть концепции в следующем. При работе предприятия происходит износ оборудования и производительность труда падает. Для замены оборудования на новое (возможно, более совершенное) необходимо на какое-то время переориентировать производство с выпуска традиционной продукции (и реализации её на рынке) на внутренние нужды.

После переоборудования предприятие входит в режим продукции с более высокой производительностью. С течением времени оборудование изнашивается, производительность падает и цикл повторяется.

В течение цикла выпуск продукции меняется. Потребность предприятия в кредитах и инвестициях зависит от фазы цикла и, следовательно, тоже меняется.

Далее мы будем понимать «переключение» в широком смысле. Так, предприятие в фазе реконструкции прекращает выпуск своей продукции (и реализацию ей на рынке), но не обязательно переключается на выпуск оборудования. Последнее (включая его монтаж) приобретается у специализированных предприятий машиностроительной отрасли. Для этого необходимы средства и время. Для реконструкции используются: оборотные средства, существующие в момент переключения, накопленные ранее резервные средства (амортизационные отчисления) и средства, взятые в кредит. Сотрудники предприятия могут частично участвовать в монтаже, или считаться в отпуске (оплаченном частично или полностью).

Цель работы – построить и исследовать базовую математическую модель работы предприятия в режиме с переключением. Эта задача является микроэкономической. В макроэкономике эффект переключения может проявляться двояко.

Во-первых, если фазы переключения синхронизованы, то в макроэкономике возникают короткие циклы (порядка 5 – 7 лет). Вариант синхронизации коротких циклов и связи их с циклами Кондратьева заслуживает специального обсуждения  и будет рассмотрена позже. На вербальном уровне связь коротких и длинных циклов обсуждается в работах [2] – [6].

Во-вторых, необходимость брать «длинные» кредиты для реорганизации существенно влияет на деятельность коммерческих банков и на финансовую систему в целом (что прямо относится к макроэкономике).

II. Модель циклической работы одного предприятия.

В качестве базовой примем модель работы предприятия, предложенную в  [7]. Она имеет вид:

(1а)

(1б)

Здесь: M’ - оборотные средства; P’ - количество продукции на складе; τ - время оборота (далее примем: τ ~ двух месяцев, одна шестая года); p_m — рыночная цена продукта; p – себестоимость; k’ - постоянные издержки; Q — объём максимальной реализации продукции на рынке; P₀ — ёмкость склада; k’ = p_m /τ_c – издержки на содержание склада (включая аренду, порчу продукции, исчерпание срока годности и т.п.); τ_{c -}   - срок годности (τ_c>> t).

Величина p_m является внешним параметром, он устанавливается в результате во всем обществе (в результате конкуренции и т.п.). В физике аналогом является т. н. «самосогласованное поле». Себестоимость p – внутренний параметр. Она зависит от уровня технологии в данной фирме и в разных фирмах различна. При реконструкции она уменьшается.

Постоянные издержки складываются из: к=к₀+к₁+к₂ , где: к₀  - коммунальные издержки, к₁  - выплаты по кредитам и к₂  - средства, откладываемые для грядущей  реконструкции (амортизационные отчисления).

В (1) все величины в натуральных единицах. Введем безразмерные переменные:

(2)

Это значит, что за единицу времени принято время производственного цикла. За единицу оборотных средств приняты средства, получаемые в результате максимальной реализации продукции  за один производственный цикл. За единицу продукции принято её количество, при котором склад заполнен на половину.

Введем безразмерные параметры:

(3)

Тогда система (1) примет вид:

.

(4)

В модели (4) возможны два стационарных состояния при значениях переменных:

(5)

Состояние M₊ , P₊ — усточивый узел, оно соответствует стабильной работе предприятия. Состояние M_{- ,} P_-  — седло; оно неустойчиво. Фазовый портрет системы (4) приведен на рис. 1. (при χ=1,3, b=5, к=k=0,03).

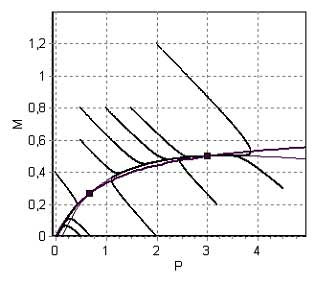
Рис. 1. Фазовый портрет системы (4).

На рисунке представлены главные изоклины:

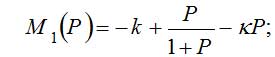
- изоклина горизонталей.

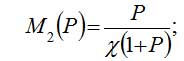
- изоклина вертикалей.                                                                    (6)

Пересечения изоклин – стационарные состояния, значения переменных в них приведены в (5). Через точку (M_-,P_-) проходит сепаратриса, отделяющая область устойчивой работы предприятия от области банкротства.

В системе (4) возможна бифуркация – слияние и исчезновение точек (M₊ ,P₊) и (M_- ,P_-) (стационарных состояний). Она имеет место при

(7)

Из выражений (5) и (7)  видно, что при увеличении  χ расширяется область стабильного существования фирмы и увеличиваются допустимые значения   коэффициента к, (в том числе резервных накоплений)

Фазовый портрет в области банкротства (но вблизи бифуркации) представлен на рис. 2. (при χ=1,25, b=5, к= 0,06;  k=0,1).

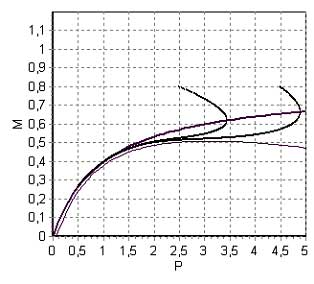
Рис. 2. Пояснения в тексте.

В этом случае вся плоскость (M,P ) оказывается областью банкротства. Однако, если предприятие работало стабильно (например, при χ=1,5, b=2, к=k=0,03; M=0,62, P=6),  но затем параметры изменились (произошла бифуркация), то изображающая точка медленно движется между изоклинами, так, что величина М почти не изменяется. Это означает, что предприятие уже вступило на путь банкротства, но внешние признаки этого почти не заметны (т.н. «скрытое банкротство»). Однако после загиба изоклин банкротство становится заметным и катастрофическим.

Учтем изменения параметра χ. В (4) он отражает состояние оборудования (т.е. его уровень технологии и износ). Износ оборудования пропорционален интенсивности его использования, т.е. выпуску продукции. Последняя пропорциональна оборотным средствам. Динамику изменений параметра χ можно записать в форме

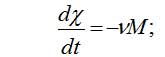
(8)

Величина ν по смыслу и размерности – обратное время износа. Последнее достаточно велико – порядка 5 — 7 лет (т.е. ν ~ 0,02-0,03τ^-1 ). В течение этого времени параметр χ изменяется от начального значения (порядка χ ~ 1,5) до бифуркационного ( порядка χ~1,2). Поэтому величина ν мала, (порядка ν~ 0,02). Этого, однако, достаточно, чтобы износ оборудования привел предприятие к банкротству.

III.  ПРИМЕР РАСЧЕТА ЦИКЛА

В качестве иллюстрации приведем пример модельного  расчета цикла по стадиям при конкретных значениях параметров. Они зависят от того, к какой отрасли относится предприятие. Так, в сырьевой отрасли России рентабельность (параметр χ ) существенно выше, чем в других отраслях. Ниже мы выбрали параметры, характерные для обрабатывающей промышленности современной России, именно: k=0,06, k₁=k₂=0,03, k =0,03, β =2, ν=0,02

В качестве начального был  принят момент возвращения фирмы на рынок с обновленным оборудованием. При этом параметр χ высок: χ (t=0) =χ₀ =1,5, склад пуст: P(t=0) =P₀=0,  оборотные средства малы и близки к критическому значению: M(t=0)= M₀= 0,3, но несколько выше сепаратрисы.

Динамика переменных , М и Р в течение цикла описывалась системой уравнений (4) и (8). Результаты представлены на рис. 3.

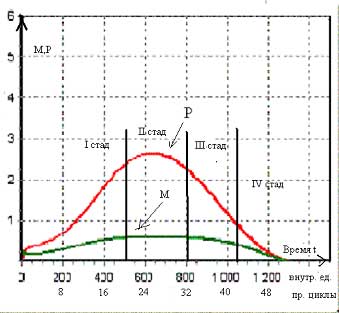
Рис. 3 По оси ординат -  оборотные средства М и продукция на складе Р в безразмерных единицах. По оси абсцисс – время во внутренних единицах (верхняя шкала) и производственных циклах τ (1τ = 2 месяца).

Цикл разделен  на четыре стадии.

Первая стадия – вход в рынок, в течение неё выплачивается долг по кредиту  Переменные M  и P  возрастают.  Видно, что стадия входа в рынок длится долго – порядка двух – трех лет (12 – 18 циклов). При этом оборотные средства достигают стационарных значений M_I = M₊ =0,64  через два года. Время T_I = 12τ ~ два года можно считать длительность первой стадии. При этом склад заполняется лишь на 70 % .

Математический смысл эффекта замедления первой стадии прост: путь от начальных значений достаточно длинный и траектория располагается между изоклинами, т.е. в каждый момент времени система близка к стационарной.

Физический смысл тоже прост: темп роста оборотных средств определяется величиной (χ1)^-1, которая больше τ=1.

Вторая стадия –  предприятие работает стабильно в течение двух – трех лет. При этом оборотные средства близки к максимальным и значения параметра χ  выше бифуркационного, но в конце стадии приближаются к таковому.

Третья стадия – параметр χ (производительность) ниже бифуркационного, так,  что эта стадия соответствует скрытому банкротству. Из рисунка видно, что оборотные средства почти не меняются, но склад опустошается. Эта стадия длится примерно два года и в конце неё появляются признаки явного банкротства.

Четвертая стадия на рисунке соответствует явному (катастрофическому) банкротству. Реально реконструкция начинается раньше и тогда четвертая стадия заменяется фазой реконструкции.

Момент начала реконструкции τ_rec может быть выбран как в начале третьей стадии (т.е. при  τ_rec =30), так и в конце неё (при τ_rec =42). Динамика величин М  и Р в течение реконструкции описываются уравнениями (4) при условии: χ =0.

Для осуществления реконструкции необходимы средства  M_rec , которые равны сумме:

M_rec =M_cr +M(τ_rec ) +M_res   - M₀                                                        (9)

Где:  M_cr  — средства, которые можно взять в кредит. M(τ_rec )    – оборотные средства, имеющиеся в наличии в момент начала реконструкции.  M_res   - средства, накопленные в течение первой и второй стадий, они  равны:  M_res   = k τ_rec .  M₀ – средства, которые необходимо сохранить до конца реконструкции, чтобы войти в рынок в следующем цикле, примем, что они равны (как и в данном цикле) M₀   =0,3.

Величина M_rec зависит от стоимости нового оборудования. Если оно качественно отличается от прежнего (за счет инноваций), то цена его высока, но  и производительность (коэффициент  χ) выше. Если оно сохраняется прежним (но не изношенным), то цикл повторяется без изменений. Выбор M_rec  ависит от руководства фирмы и моделью не предопределяется.

Величины M(τ_rec ), P(τ_rec) и M_res. зависят от выбора момента начала реконструкции. В случае ранней реконструкции (τ_rec =30) третья стадия практически отсутствует. При этом: M(τ_rec ) =0,6,  P(τ_rec ) = 2, M_res   = 0,54, M_cr=0,3, M₀ =0,3. и M_rec  =1,14. Динамика переменных М  и Р  в течение реконструкции представлена на рис. 4а.

В случае реконструкции после третьей стадии: M(τ_rec ) =0,5,  P(τ_rec ) = 0,5,  M_res   = 0,9, M_cr=0,3, M₀ =0,3 и M_rec   =1,4. Динамика представлена на рис. 4б.

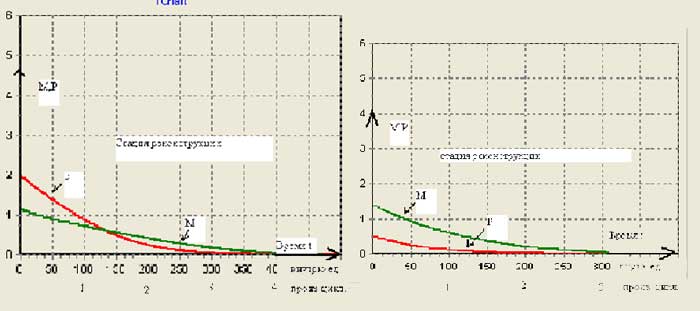
Рисунок 4.
Зависимости переменных М  и Р от времени. а) При раннем начале реконструкции (τ=30~5лет). б) при поздней реконструкции ((τ=42~7лет). По оси абсцисс время в «шагах» и в единицах τ.

Из изложенного можно сделать следующие выводы.

1.  Время реконструкции должно быть достаточно малым – порядка полугода. В противном случае наступает банкротство. Это время слабо зависит от имеющихся в запасе средств и выбора начала реконструкции.
2. Из сравнения рис. 4а и 4б следует, что динамика величины Р существенно зависит от времени начала реконструкции. При поздней реконструкции склад быстро истощается. При ранней реконструкции склад сохраняется до середины реконструкции. Это позволяет фирме сохранить  свою «марку» и место на рынке, не смотря на отсутствие производства товаров. Эффект сохранения «марки» в модели явно не учитывается, но в реальности играет существенную роль.
3. В приведенном примере принято, что в результате реконструкции параметр χ принимает то же значение, что и в начале цикла , т.е оборудование обновляется, но не совершенствуется. В этом случае цикл повторяется буквально и фирма работает стабильно, но не развивается. В случае, когда оборудование совершенствуется (за счет инноваций), фирма работает циклически, но с положительным трендом.
   В общем случае параметры могут меняться и в худшую сторону (например, за время цикла кредитная ставка увеличилась). Тогда фирма будет работать циклически, но с отрицательным трендом.
   4 Фаза реконструкции обладает рядом важных особенностей.
   Во-первых, идеи Шумпетера могут реализоваться именно в этой стадии. Даже «новатор» не будет вводить инновации в первой и второй стадиях, когда оборудование недавно обновилось.
   Во-вторых, именно в этой стадии решается судьба фирмы. Слабые внешние воздействия могут кардинально изменить ситуацию: фирма либо возвращается на рынок, либо терпит банкротство. Предусмотреть малые флюктуации невозможно, поэтому в динамической модели появляется понятие – вероятность.
   В других стадиях цикла изменения условий (параметров) влияют на работу фирмы, но слабо, в меру малости изменений.
   В-третьих, роль руководства фирмы особенно важна в стадии реконструкции. Принятие решения о начала стадии и способ распоряжения средствами M(τ_rec ) зависит от целей и стратегии руководства. Модель не может заменить сам акт принятия решения, но может служить инструментом поддержки его.
   Математический смысл перечисленных свойств в том, что в фазе реконструкции фирма находится вблизи сепаратрисы. Из этого следует также, что считать эту стадию «мгновенной» (и редуцировать как «быструю» по Тихонову) в общем случае нельзя.
4. Необходимость реконструкции  влияет на деятельность коммерческих банков. Это можно проследить на основе уравнения (9).
   Если во всех фирмах  M_rec < M(τ_rec ) +M_res   - M₀, то  потребность в кредитах отпадает. Банки лишаются  основного источника доходов – получения процентов по «длинным» кредитам. Последнее имеет место при стабильной работе всех фирм без развития и освоения инноваций.
   Если  M_rec > M(τ_rec ) +M_res   - M₀ , то кредиты необходимы. Последнее имеет место , если при реконструкции  используются дорогостоящие инновации. Кредиты (и инвестиции) особенно необходимы  новым (новаторским ) фирмам, которые только входят не рынок  и средства M(τ_rec ) +M_res  у них отсутствуют.
   Т.о. в развитой, стабильной макроэкономике роль банков в производстве практически отсутствует. Банковская система начинает играть роль  только при развитии.

 Заключение.

Обсудим основные выводы.

1. Идея цикличности развития фирмы играет важную роль в эволюционной экономике. Идеи Шумпетера дополняются положением: новатор должен правильно выбирать момент внедрения инноваций.
2. Успех новатеров (или консерваторов) зависит от фаз волн Кондратьева. На восходящих фазах преобладают новаторы, на нисходящих – консерваторы.
3. В предлагаемой работе фаза реконструкции рассмотрена в первом приближении. Уже из неё ясно, что эта фаза играет важную роль и потому заслуживает более детального изучения.

В работе рассмотрен пример работы предприятия в обрабатывающей отрасли промышленности России. Модель можно использовать и в других отраслях, но при другом наборе параметров. При этом модель не позволяет предложить универсальный алгоритм оптимального управления. Модель претендует на роль инструмента поддержки принятия решения, работающего в диалоговом режиме.

Работа поддержана программой ФАНО 14-11-00634 на 2014 год.

Литература.

1. Маевский В.И., Малков С.Ю., Режим переключающегося воспроизводства в экономике., Материалы IX Международного симпозиума по Эволюционной Экономике., Москва – СПб, Из-во «Нестор-История»,2013 г. стр.114-137.
2. Туган-Барановский М.И., «Периодические промышленные кризисы». Избранные труды, М., Наука,1997 г.
3. Гринин Л.Е. Каратаев А.В., Цирель С.В., «Циклы развития современной Мир-Системы», М., УРСС,2011 г.
4. Гринин Л.Е. Каратаев А.В., « Циклы кризисы, ловушки современной «Мир -Системы», М., УРСС,2012 г.
5. Перес Карлотта, «Технологические революции и финансовый капитал», Москва, «Дело»,2011 г.
6. Чернавский Д.С., Старков Н.И., Малков С.Ю., Коссе Ю.В., Модель циклов Кондратьева, Материалы IX Международного симпозиума по Эволюционной Экономике., Москва – СПб, Из-во «Нестор-История,2013 г. стр. 166-173.
7. Чернавская Н.М., Щепетов Д.С., Васильева Л.Ю., «Переход предприятия к оптимальному режиму работы. Фундаментальные физ-мат проблемы. Из-во МГТУ «Станкин»,2007 г. , т. 7, стр. 269-275.