В настоящей статье изложен научный подход Дмитрия Сергеевича Чернавского к вопросам моделирования экономических процессов. Излагается история работы Дмитрия Сергеевича на экономическом направлении, ее основные этапы и достижения. Одним из важнейших достижений в области экономического анализа стало предсказание группой ученых, возглавляемых Д.С.Чернавским, основных кризисов, произошедших в нашей стране за последние 20 лет, а именно, дефолта 1998 года, кризиса промышленного производства второй половины 2000-х, кризиса 2008 года и последовавшей за ним рецессии. В качестве примера динамического анализа мировых макроэкономических процессов приведена модель функционирования доллара в качестве мировой валюты. На данном конкретном примере показана возможность сеньёража за счет эмиссии доллара и рассчитано «окно возможностей», которое позволяет эмитировать доллары в качестве мировой валюты без ущерба для собственной экономики.

Как пример динамического анализа экономики отдельного государства рассматривается модель  развития закрытого общества (без внешних экономических связей) в однопродуктовом приближении. Модель основана на принципах рыночной экономики, то есть динамика цены определяется балансом спроса и предложения. Показано, что в общем случае состояние рыночного равновесия не единственно. Возможно несколько стационарных состояний, отличающихся уровнем производства и потребления. Рассмотрен эффект адресной денежной эмиссии в низкопродуктивном состоянии. Показано, что в зависимости от ее размера и адреса она может привести как к переходу в высокопродуктивное состояние, так и просто вызвать инфляцию без перехода. Обсуждается связь этих результатов с «кейнсианским» и «монетаристским» подходами.

Введение.

В 1990 году встретились ученый-физик и производственник-практик. Разговорились они о судьбе страны (тогда еще СССР), о путях ее экономического и политического развития.

Время тогда было смутное: перестройка, гласность, бурные дебаты в прессе. Кооперативы всех мастей все более отвоевывали себе место под экономическим солнцем. Трудовые коллективы избирали себе по конкурсу директоров, брали в аренду цеха и целые предприятия.

Все это словоблудие и «экономическая пена» служили дымовой завесой для развала системы в интересах высших партийных элит прежних советских республик.

Призывы к гласности и демократии чаще всего предшествуют свержению существующей власти — к такому выводу пришли физик и производственник. И возникла идея – а не построить ли модель советского общества. Так родился знаменитый «двугорбый верблюд» (статья Чернавского Д.С. «У верблюда два горба, потому что жизнь – борьба», газета «Солидарность» №9-10, М. 1991г. [1]). Так родилась наша группа, объединенная идеей математического моделирования социальных и экономических процессов в обществе, под руководством Чернавского Д.С.

К сожалению, прогнозы о скором развале СССР, сбылись и в 1991 году мы оказались в совершенно другой стране.

В это время, в среде экономистов шла оживленная дискуссия о необходимой либерализации цен. Наша группа выступала против либерализации, так как модель, теперь уже российского, общества показывала, что это приведет к росту цен за короткий период в десятки раз и обнищании основной массы населения. Так и случилось в 1992 году в результате «Гайдаровских реформ».

С 1992 года наша группа организационно оформилась в виде Лаборатории экономической синергетики. Мы активно сотрудничали с рядом коммерческих и производственных структур, делали аналитические обзоры для Министерства экономики, Министерства труда, Министерства обороны и других ведомств.

Своим главным достижением мы считали умение, на основе построения математической модели, прогнозировать развитие социально-экономических процессов, в том числе. момент наступления «катастрофических» явлений как на уровне экономики страны в целом, так и на уровне отдельного предприятия.

Примерами такого прогнозирования может служить, например, крах фирмы «МММ», который мы просчитали за четыре месяца до обвала пирамиды Мавроди. Второй пример – осенью 1997 года в журнале «Полития» № 3(5) в статье Чернавского Д.С. и Щербакова А.В. «Экономика России: стабилизация или застой» [2] был, с точностью до месяца, предсказан дефолт 1998 года.

С 1999 года в экономике России произошла стабилизация и некоторый рост. Этот рост был воспринят рядом экономистов как начало «экономического чуда», был даже провозглашен тезис об удвоении ВВП в ближайшем будущем. Наш анализ показал, что только целенаправленное государственное регулирование может привести к действительному росту экономики. В противном же случае рост остановится и сменится стагнацией реального сектора экономики. Процесс этот займет 4-5 лет. Действительно, после 2003 года рост в реальном секторе ощутимо замедлился и во многих отраслях наметился спад.

Спад начала 2000-х вылился в очередной кризис в 2008 году. Сам кризис был предсказан нами за полгода (в апреле 2008 г.), а его причины и последствия были описаны в ряде аналитических работ 2009-10 г.г.

К 2014 году наша группа переросла за рамки лаборатории. Было принято решение организовать Центр социально-экономического прогнозирования им. Д.И.Менделеева. В настоящее время, в рамках Центра работает несколько десятков видных российских ученых — специалистов в области экономики, социологии, анализа сложных динамических систем.

К величайшему сожалению, летом 2016 года не стало одного из основателей и научного руководителя Центра Дмитрия Сергеевича Чернавского. Настоящая статья посвящена его вкладу в изучение динамических процессов в экономике.

I. Окно возможностей или модель сеньёража.

Одним из направлений динамического моделирования экономики является моделирование финансовой системы, в частности мировых финансов. Ниже изложена модель, описывающая поведение доллара в качестве мировой валюты. Впервые данная модель была опубликована в 2015 году [3].

Обсудим вербальный сценарий процесса.

В каждой стране, взятой отдельно, эмиссия валюты ограничена условием Фишера:

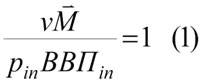
Здесь: ВВП – количество товара (агрегата товаров), производимых в год в естественных единицах («штуках»), цена (в национальной валюте) единицы агрегированного товара на внутреннем рынке, γ – скорость производства (γ-1/τ где τ – время производственного цикла, – оптимальное значение объема денежной массы. Отметим, что реальное значение может существенно отличаться от оптимального.

Смысл условия Фишера – обеспеченность национальной валюты произведенной продукцией внутри страны.

Динамика эмиссии валюты описывается логистическим уравнением:

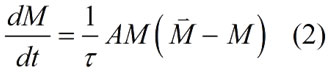
Стационарное (равновесное) решение уравнения (2): M = . Параметр А имеет размерность обратную М и по порядку величины: .

Учтем эффект участия национальной валюты в международной торговле в качестве мировой валюты (далее для конкретности будем считать, что М – доллары США). Тогда количество этой валюты и её равновесное значение должно быть больше: _tot = M + ΔM, где ΔМ = b_ex p_ex ВВП_exτ_ex – дополнительная эмиссия национальной валюты с целью захватить внешний рынок. Здесь: p_ex — цена товара (в долларах) на вешнем рынке, она отличается от внутренней цены p_in и может сильно меняться (в то время как pin поддерживается постоянной), ВВП_ex – объем внешней мировой торговли и τ_ex – характерное время внешнеторгового оборота. Коэффициент b_ex отражает стремление захватить внешний финансовый рынок (т.е. экспансию доллара) и сам зависит от объема долларовой массы М, поскольку увеличение её способствует этому стремлению Далее мы примем: b_ex= bM.

Использование национальной валюты в мировой торговле выгодно стране – эмитенту, поскольку импортные товары оплачиваются в долларах, а последние эмитируются. Т.о. страна-эмитент получает импортные товары фактически бесплатно, за счет дополнительной эмиссии. Эти средства уходят во внешний мир и не влияют на внутренние цены. Это явление известно давно (еще со средних веков) и имеет название – «сеньёраж».

Если та же валюта начинает использоваться внутри других стран (например, в качестве резервных фондов), то эти страны попадают в зависимость от страны-эмитента. Пока внешняя цена p_ex стабильна, то такая ситуация не вызывает опасений. Однако, она может оказаться неустойчивой. Тогда при росте эмиссии и росте цен p_ex доллар обесценивается – его «курс» падает. Вместе с этим обесцениваются и резервные фонды других стран, что равносильно экономической катастрофе мирового масштаба

Понятие «курс» имеет смысл при обмене валют. Т.н. «справедливый» курс определяется из условия: при обмене валют покупательная способность должна сохраняться. Тогда курс доллара по отношению, например, к евро, равен: Q($/e) = p_e/p_ex. Реальный обменный курс, как правило, далек от «справедливого», но общее положение: курс доллара – величина, обратно пропорциональная цене p_ex остается в силе.

Таким образом основная задача модели – оценка устойчивости ситуации, когда доллар претендует на роль мировой валюты и описание процесса вблизи бифуркации.

Математическая модель

В качестве динамических переменных выберем денежную массу (долларов) М и цену p_ex . Уравнение для М на основании изложенного выше запишем в виде:

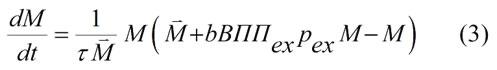
Уравнение для p_ex запишем. Исходя из положений: с ростом денежной массы p_ex растет, но при больших значениях p_ex этот рост тормозится. Тогда в простейшем случае уравнение имеет вид:

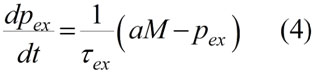
Здесь параметр a отражает степень роста p_ex с возрастанием М. Размерность параметра a – обратные «штуки» и по порядку величины , где α – безразмерный параметр порядка единицы (но может быть и много меньше), τ – время установления цен на внешнем рынке.

Введем безразмерные переменные и параметры:

x = M/ ; y = p_ex/p_in; β = bp_inВВП_ex;

Время будем измерять в единицах τ

Тогда уравнения (3) и (4) примут вид:

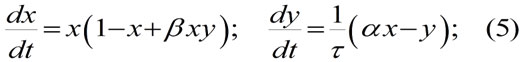
Фазовый портрет этой системы представлен на Рис. 1. Изоклины вертикалей

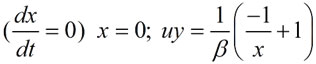
и изоклина горизонталей

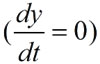– прямая линия: y = αx. Пересечения изоклин (стационарные состояния) имеют место при:

.

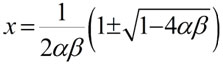При 4αβ < 1 существуют два стационарных состояния. Фазовый портрет представлен на Рис 1. Первое состояние — устойчивый узел. Оно соответствует умеренной экспансии доллара, когда дополнительная эмиссия не происходит. Это состояние устраивает всех, кроме США, поскольку сеньёраж при этом тоже практически исчезает.

Второе состояние неустойчиво – седло. Через него проходит сепаратрисса, отделяющая область притяжения устойчивого состояния от области безудержного роста долларовой массы и цен, т.е. экономической катастрофы.

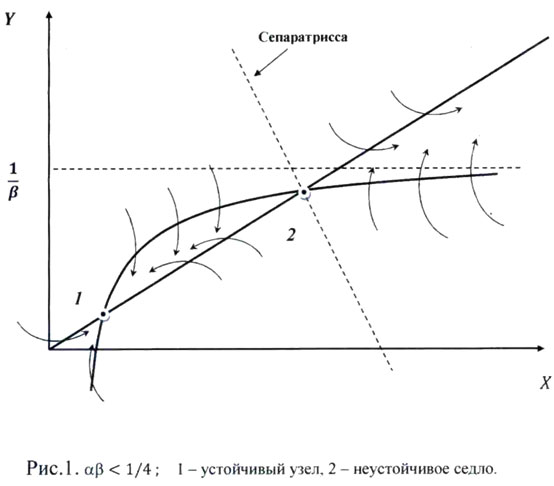
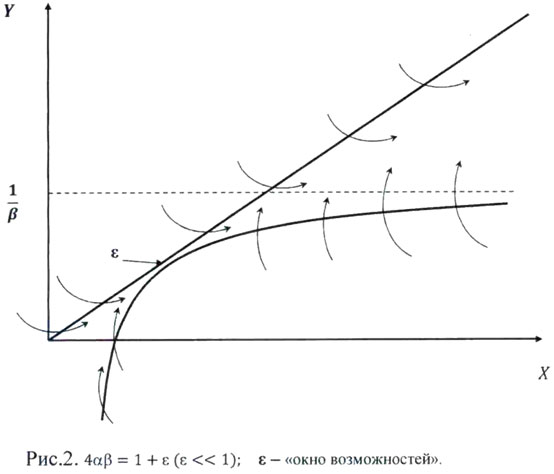
При увеличении параметров до αβ = 1/4 происходит бифуркация – слияние седла с узлом. При 4αβ = 1 + ε (ε << 1) стационарные состояния исчезают и всё фазовое пространство становится областью притяжения катастрофы, что представлено на Рис.2. Однако, если ε мало и изоклины близки друг к другу (открывается т.н. «окно возможностей» для сеньёража), то изображающая точка движется к катастрофе медленно (по закону , что создает иллюзию стабильности. Однако, с течением времени (когда ) медленное движение переходит в быстрое и это воспринимается уже как реальная катастрофа.

Таким образом управляющим параметром («параметром порядка») является произведениеαβ (или в размерных единицах: ). Эти параметры сами меняются со временем, но медленно. Динамика их изменений определяется не только экономикой, но также политическими и военными факторами. При этом разные страны преследуют разные цели. США стремятся увеличить долларовую экспансию (параметр b) и, одновременно, поддержать курс доллара при увеличении (уменьшит параметр a) с целью получения стабильного сеньёража.

Другие страны стремятся ограничить давление сеньёража. С этой целью они пытаются (где можно) использовать свою валюту в международной торговле (уменьшить ВВП_ex, обслуживаемый долларами и, тем самым, параметр β). Эти попытки пресекаются политическими (давление США на Евросоюз) и военными (война в Ливии, Ираке и т.п.) методами. В результате управляющий параметр колеблется, оставаясь в среднем постоянным.

По нашим оценкам упомянутая выше бифуркация уже произошла примерно 20 лет назад и Мир уже встал на путь краха доллара. На это обратил внимание М. Хазин (в чем был прав). Однако, он не учел эффект «окна возможностей» и предсказал немедленное падение курса доллара. В течение последних 20 лет происходило медленное движение через «окно» и сейчас Мир близок к выходу из него, т.е. быстрому (катастрофическому) падению курса доллара. Последнее может произойти в течение ближайшего года-двух.

Подставив в систему уравнений (5) конкретные макроэкономические параметры, получаем решение, изображенное на Рис.3.

Решение наглядно демонстрирует наличие «окна возможностей» для доллара в течение 20 лет. По истечении этого срока происходит «катастрофа».

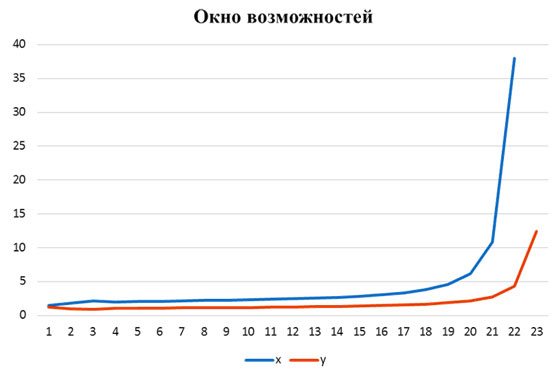
Рис. 3 Решение системы уравнений (5), демонстрирующее существование «окна возможностей» для доллара в течение 20 лет.

II. Динамическая модель закрытого общества (институциональные ловушки и кризисы).

Вопрос о самоорганизации рыночной экономики в самодостаточной (то есть обеспеченной собственными ресурсами) стране является сейчас одним из актуальных в макроэкономике [5]. Это вопрос — часть более общей проблемы, касающейся взаимодействия нескольких стран с различной экономикой. Он обсуждался многократно в работах классиков [6], с ним cвязаны направления макроэкономической теории: монетаристское [7], кейнсианское [8], концепция Ларуша [9].

Общество — сложная динамическая система. Результаты его эволюции зависят от многих составляющих, среди которых важную роль играет то, каковы условия функционирования экономических субъектов: свободный ли это рынок или рынок с элементами государственного регулирования, авторитарная это система или какая-то их смесь. Но даже если конкретные условия (тип экономики) заданы и, скажем, одинаковы у двух стран, конечные результаты их развития могут оказаться прямо противоположными. Решающая роль в определении результата эволюции, при прочих равных условиях, принадлежит уровню экономического развития общества. Косвенным подтверждение этого может служить наличие множества различных моделей, призванных описать поведение общества, и дающих прямо противоположные друг другу результаты. На самом деле между этими моделями нет противоречия, просто они описывают поведение одной и той же сложной системы (рыночная экономика) в разных состояниях и делают это без учета динамического поведения общества и его структуры.

Для решения данной проблемы необходимо опираться на математическую модель динамики процесса. Такой подход развивался за рубежом [10], но затем интерес к нему ослабел. Сейчас он активно развивается в России и представлен в монографиях [11,12].

Во всех моделях необходимым элементом должно быть описание не только стационарных состояний, но и переходных процессов, которые сейчас являются наиболее актуальными, поскольку именно с ними связано поведение государств, испытывающих кризис.

Мы обратим внимание на два обстоятельства, которые, как нам кажется, могут играть важную роль в формировании кризисных процессов.

Во-первых, в большинстве современных экономических моделей, претендующих на количественное описание, явно или неявно предполагается существование единственного устойчивого равновесного состояния, при отклонении от которого, общество возвращается к нему под влиянием рыночных процессов или регулирования. При этом не учитывается тот факт, что в реальном рыночном обществе могут существовать несколько равновесных состояний с различными экономическими показателями. Среди них могут быть и неблагополучные. Последние получили название «институциональные ловушки» [13]. Отметим, что классики экономики хорошо понимали это обстоятельство, хотя и не могли описать его на математическом языке [14], однако затем оно было забыто, интерес к нему появился лишь в последнее время. Выведение общества из одного состояния устойчивого равновесия может перевести его в такую область, откуда оно будет стремиться к другому равновесному состоянию. Более того даже плавное изменение макроэкономических показателей общества может приводить к тому, что прежнее равновесное состояние исчезнет и тогда общество заведомо будет стремиться к другой точке равновесия, находящейся может быть очень далеко от предыдущей. В обоих случаях такие, внешне кажущиеся неожиданными, процессы воспринимались бы как кризис или «экономическое чудо».

Во-вторых, как показано в целом ряде работ [15], на динамическое поведение общества существенное влияние оказывает экономическая структура общества (ЭСО). Под ЭСО мы понимаем распределение элементов общества (семей) по ликвидным накоплениям. Она играет важную роль в балансе спроса и предложения на товары, услуги, финансы и т.д. В традиционных макроэкономических моделях на количественном уровне как правило рассматривается только одна группа потребителей и одна группа производителей, формирующих спрос и предложение. Пересечение соответствующих кривых, например, в координатах цена-объем, определяет значение равновесной величины макроэкономического показателя. Такой подход фактически означает замену рассмотрения распределенных величин спроса и предложения на рассмотрение соответствующих средних. Эта замена с математической точки зрения правомерна для распределений близких к нормальному и вблизи положения равновесия. Если система находится вдали от точки равновесия или распределение существенно отличается от нормального, например, является двугорбым как в современной России, ограничение рассмотрения только анализом средних величин может привести к неверным значениям макроэкономических показателей, отличающимся на порядки величин от действительных, а динамика поведения реального общества может качественно отличаться от модельного.

Два приведенных выше замечания особенно важны для обществ, находящихся в состоянии кризиса и/или реформирования, поскольку именно в эти периоды макроэкономические показатели претерпевают значительные изменения, а имущественное расслоение общества увеличивается. Примером такого общества является, в частности, Россия.

До сих пор были рассмотрены только незамкнутые варианты модели, в которых не учитывалось влияние производства и товарооборота на ЭСО [15]. Рассмотрим простейшую модель, в которой только через механизм взаимодействия спроса и предложения учитывается как прямая так и обратная связь процессов производства-потребления и ЭСО. Такая модель позволяет ответить на следующие вопросы

1) Существует ли стационарное состояние общества, если существует, то единственно ли оно,  и при каких условиях устойчиво.

2) Какова стационарная структура общества (унимодальна или бимодальна), как она зависит от продуктивности и как последняя зависит от нее.

Рассматривается вариант закрытого общества, в котором экспорт и импорт товара отсутствует.

Основные положения модели.

1) Рассматривается производство и потребление одного продукта (так называемое однопродуктовое приближение). Его можно рассматривать как стандартную совокупность товаров, в которой коэффициенты предпочтения зафиксированы и одинаковы для всех слоев общества.

При этом в процессе обмена деньги фактически жестко связаны с продуктом, поэтому экономические показатели такие как прибыль, объем производства и потребления и т.п. можно исчислять как в денежных, так и в натуральных (штуках, килограммах и т. д.) единицах. Действительно, деньги, как универсальный товар, играют особую роль только, если число различных товаров велико. В этом случае прямой обмен приводит к проблеме факториальной сложности, для преодоления которой, собственно, и были введены деньги. В процессе же потребления роль денег и товаров различается т.к. потребление товаров приводит, а потребление денег не приводит, к их выбыванию из обращения.

Цену продукта в дальнейшем будем обозначать р.

2) Рассматривается общество, состоящее из двух групп

I. Производители (работники), число которых обозначим n’, работающие на предприятиях собственников. В их число мы включим не только непосредственных производителей, но также обслуживающий персонал и служащих, занятых в инфраструктуре, охране и поддержании стабильности всего общества. Все они объеденены тем, что их доход — зарплата P_n, отличная от доходов второй группы.

II. Организаторы (они же «собственники» или “владельцы”), число которых обозначим m’, получающие доход от продажи произведенного на их предприятиях товара и выплачивающие зарплату P_n членам первой группы. Доходы «собственников» обозначим P_m. В их число включены также “посредники” и торговцы, живущие за счет прибыли, но не зарплаты.

Накопления семей первой и второй групп обозначим U_n‘ и U_m‘, соответственно.

Доходы и накопления членов разных групп различны, но внутри каждой группы будем считать их одинаковыми.

В такой модели ЭСО представляется в виде двух узких пиков (горбов). Реально горбы размыты и если расстояние между ними больше их ширины, то ЭСО бимодально. Если горбы близки, то общество практически унимодально.

В модели структура общества зависит от двух параметров: относительной численности s=n/m и отношения доходов D=P_m/P_n ( или накоплений U_m/U_n ). Последнее отражает относительное расстояние между горбами то есть модальность общества.

3) Примем, что необходимые для производства ресурсы (полезные ископаемые, посевные площади и т.п.) находятся в избытке. При этом можно считать, что “безработные” в обществе отсутствуют. Отсюда следует, что рынок труда в модели фактически отсутствует. При этом численности n’ и m’ определяются не балансом на рынке труда, а экономической целесообразностью, зависящей от уровня технологии производства и его организации. Далее это отношение будем считать заданным.

4) Будем считать, что объем денег в обществе равен М, а количество семей равно N, причем числа M и N фиксированы. Т.о. справедливы “законы сохранения” людей (n’ + m’ = N) и денег (n’U_n + m’U_m = М). Далее удобно использовать относительные численности: n=n’/N и m=m’/N, и относительные накопления (покупательные способности накоплений): r_n=U_n/p и r_m=U_m/p. Тогда законы сохранения можно представить в виде

                   (6)

где  средние накопления и относительные средние накопления.

5) В дальнейшем важную роль будет играть функция производства , то есть количество продукта (в естественных единицах, например, в штуках), производимое в обществе в единицу времени. Оно зависит от числа производителей Nn и от капиталовложений S. В нашей модели функция производства обладает следующими свойствами:

i ) Она пропорциональна числу производителей, то есть

                                  (7)

Здесь F(S) — удельная производительность труда, т.е. выработка, приходящаяся на одного работника в единицу времени.

ii) Капиталовложения (производственные затраты) зависят от накоплений в обществе. В первую очередь их делают “владельцы” и их объем зависит от накоплений r_m Накопления “служащих” также могут быть использованы для инвестиций через банковскую систему. В этом случае доходы последних, помимо зарплаты, включают проценты по вкладу. Однако, в данной работе мы не будем учитывать эту взаимосвязь, то есть примем, что банковская система и рынок денег отсутствуют[1]. Далее будем инвестиции исчислять в реальных единицах и считать, что они зависят от реальных накоплений r_m. С ростом накоплений вложения увеличиваются. Примем в первом приближении, что вложения пропорциональны накоплениям.

В однопродуктовой модели все затраты владельцев в конце концов идут на зарплату «рабочих». К ним относятся непосредственные участники производства, ремонтные рабочие, а также все рабочие и служащие бюджетной сферы (транспорт, правоохранительные органы и т.д.). Далее будем считать, что их зарплата одинакова и соотношения их численностей заданы.

iii) Производительность труда растет с ростом затрат, но не может быть больше некоторой величины F_max, определяемой уровнем техники. Примем, что производственная функция имеет кусочно-линейный характер

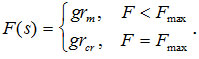                                                                          (8)

Здесь r_cr = F_max/g — величина накоплений, выше которой прямые вложения в производство не приводят к росту выпуска товара.

iv) Капиталовложения S в нашей модели пропорциональны объему производства S = n×s = n/b×F. Здесь s -капиталовложения (в штуках товара), приходящиеся на одного работника в единицу времени. Коэффициент b>1 отражает уровень рентабельности, равный (b-1)×100%.

6) Функцию потребления продукта обозначим Q(p,U). Здесь U — накопления семьи, а Q — количество продукта, приобретаемого за цену p при накоплениях U в единицу времени. В силу масштабной инвариантности функция Q(p,U) зависит от отношения r=U/p, т.е. от покупательной способности накоплений.

В нашей модели функция потребления Q(r) зависит от трех параметров, качественно характеризующих ее поведение. Она ограничена сверху максимальными потребностями в продукте в единицу времени: Q(r) < Q₀. Другой важный параметр — положение точки перегиба. По смыслу этот параметр задает отношение накоплений к цене, при котором люди начинают активно приобретать товар. Третий параметр — ширина переходной области, где люди приобретают товар, но не могут удовлетворить свои потребности в нем полностью. Мы представим Q(r) в форме

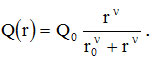                                                                                       (9)

Положение точки перегиба определяется параметром r₀, а ширина переходной области зависит от параметра n.

При ν=1 функция Q(r) всюду выпукла, что характерно для товаров первой необходимости. При ν ≥ 2 функция потребления имеет сигмоидную форму, что характерно для промышленных товаров долговременного пользования. При ν >> 1 ширина переходной области стремится к нулю и функция приобретает пороговый характер. В расчетах, приведенных в данной работе, мы приняли ν=2.

Кроме основной зависимости, описываемой формулой (9) мы учтем наличие товаров различного качества и возникающее по этой причине возрастание потребностей при росте накоплений, введя дополнительный член ε⋅r. Таким образом

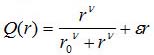
7) Зарплата P_n в натуральных единицах, которую производители получают от «владельцев» в единицу времени, зависит от капиталовложений.  В силу сохранения общего объема денег, ее величина равна капиталовложениям. Таким образом P_n=s:

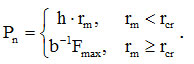                                                                        (10)

Здесь нами введен параметр h=g/b, который показывает долю накоплений собственников, выделяемую в виде капиталовложений S_v при r_m<r_cr на одного работника в единицу времени. Зарплата в денежном выражении равна P_n⋅p.

Формулировка модели.

Динамику общества мы будем описывать зависящими от  времени переменными. В качестве таковых мы используем:

1) Накопления “служащих” U_n.

2) Количество продуктов, хранящихся на складах. Эту величину мы обозначим R.

3) Цену товара p.

Динамика накоплений U_n определяется балансом доходов и расходов членов первой группы:

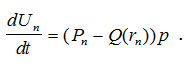                                                                               (11)

Величина U_m не является независимой переменной и определяется из закона сохранения денег (6):

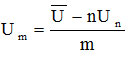                                                                                                  (12)

Здесь уместно сделать замечание. Динамика доходов и расходов в натуральных единицах определяется уравнением, отличным от уравнения (11), и имеет вид

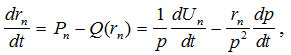
откуда получаем

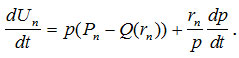                                                                (13)

Последнее слагаемое правой части соответствует индексации зарплаты при ценовой инфляции, но без дополнительной эмиссии денег (величину М мы полагаем постоянной). Мы будем считать, что владельцы без принуждения такой индексации не проводят.

Другая независимая переменная — запасы продукта R. Динамика запасов определяется балансом поступлений продуктов на склад и реализацией их на рынке [10]:

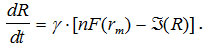                                                                           (14)

Здесь  - количество продуктов, поступающих на рынок в единицу времени; γ - безразмерный коэффициент, характеризующий быстроту отслеживания складом ситуации на рынке.

Третьей независимой переменной является цена p. Динамика цены определяется балансом спроса и предложения:

                 (15)

Здесь  - дисбаланс предложения и спроса. Величина N×[nQ(r_n) + mQ(r_m)] представляет собой платежеспособный спрос и N× - объем предложения. Обе величины выражены в естественных единицах товара, потребляемого или предлагаемого в единицу времени, которая соответствует времени потребления (или амортизации) товара τ_q. Обычно таковым считается год, что в случае производства сельхозпродукции оправдано. Изменение цены в единицу времени выражается в рублях за единицу товара и за характерное время установления рыночного равновесия τ_p. Последняя заметно меньше времени цикла потребления.

Коэффициент α содержит отношение времен τ_p/τ_q и имеет размерность (единица товара)^-2×руб. Его можно представить как комбинацию величин:

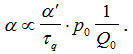
Здесь p₀ — эффективная цена, Q₀ потребление в единицу времени, α‘ — безразмерный параметр порядка единицы.

Сделаем несколько замечаний.

i) В (15) принято, что динамика цен пропорциональна дисбалансу спроса и предложения. В действительности зависимость может быть более сложной, но она должна быть нечетной по дисбалансу так, чтобы знак дисбаланса совпадал со знаком производной. В (15) выбран один из простейших вариантов.

ii) В (15) дисбаланс выражен в естественных единицах. Возможен вариант, когда цены реагируют на дисбаланс в денежном выражении, Тогда (15) примет вид  . В обоих случаях стационарные состояния соответствуют условию dis=0 и топологическая структура решений модели будет одна и та же, но динамика стремления к стационарному состоянию будет несколько различаться. В данной работе мы ограничимся моделью (15).

Далее будем считать, что ситуация на рынке отслеживается складом достаточно быстро (т.е. γ>>1). Тогда переменная R быстро приходит к своему стационарному значению и на основе теоремы Тихонова уравнение (14) можно заменить соотношением  = nF(R_m). В этом приближении конкретный вид функции  уже не важен. Уравнение (15) при этом примет вид

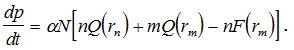                                                          (16)

Обсудим смысл уравнений (11) и (16).

Уравнение (11) показывает, что спрос производителей удовлетворяется в соответствии с их запросами nQ(r_n). В уравнении (12) с другой стороны видно, что и запросы собственников удовлетворяются полностью в соответствии с их накоплениями. Таким образом, в нашей модели платежеспособный спрос потребителей на товары всегда удовлетворяется.

В рассматриваемом варианте модели производственная функция при малых накоплениях собственников пропорциональна r_m. Это означает, что собственники выделяют средства на производство при любой (даже самой малой) величине накоплений. Более последовательной была бы модель, в которой выделение средств на производство происходит только при r_m > r_cr > 0. При r_m < r_cr в этой модели могло бы происходить уменьшение расходов за счет их полного прекращения.

Связь уравнения (14) с другими моделями установления цены (основанными на принципе максимума прибыли) мы обсудим ниже.

Для дальнейшего рассмотрения удобно ввести безразмерные переменные:

                      (17)

Здесь p₀ = /r₀. (Далее штрихи опустим, то есть будем считать, что r₀ = 1 и Q₀ =1).

Величины r_nи r_mсогласно (6), (12) и (17) зависят от х и у:

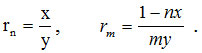                                                                              (18)

Уравнения (11) и (15) в переменных х и у принимают вид:

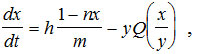                                                                                (19)

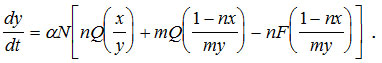                  (20)