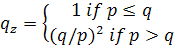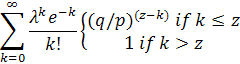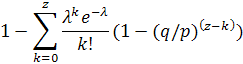Актуальность безналичных платежей продолжает оставаться высокой. Смотри Bitcoin: A Peer-to-Peer Electronic Cash System, Satoshi Nakamoto, а также A Bitcoin Primer, by CoinLab.com, Authors: Chris Koss, Mike Koss.

Ниже приведенный текст базируется на материалах выше названных статей и Википедии.

Технология bitcoin была предложена в 2009 году.

В апреле 2011 году в журнале Forbes Magazine появилась статья Andy Greenberg «Crypto Currency» (http://www.forbes.com/forbes/2011/0509/technology-psilocybin-bitcoins-gavin-andresen-crypto-currency.html), в которой были описаны возможности технологии bitcoin.

Номинальная стоимость bitcoin может лежать в пределах от десятков центов до 30 долларов США. В последнее время верхняя граница цены bitcoin далеко перешагнула рубеж тысячи долларов. Для генерации bitcoin стали использовать специальные много ядерные компьютеры.

Bitcoin-адрес подобен счету в банке, где пользователь может хранить и откуда может посылать Bitcoins. Публичные ключи, или адреса биткойн выполняют функцию конечных точек при отправке и приёме денежных средств. Адреса в текстовой форме представляют собой строки длиной около 34 символов, состоящие из букв латинского алфавита и цифр. Безопасность Bitcoin обеспечивается за счет криптографии с открытым ключом. Каждый адрес состоит из общедоступного и секретного ключа, последний должен храниться в тайне. Любой может послать Bitcoin любому при известном его общедоступном ключе, но только владелец секретного ключа может потратить эту сумму. Хотя адрес является общедоступным, никто не знает, кому принадлежит тот или иной адрес. Bitcoin-адреса являются псевдонимами.

Для криптографической защиты сектетных частей документов протокол Bitcoin использует самый надежные алгоритмы NSA (National Security Agency). Любой участник может сформировать любое число адресов бесплатно. Существует примерно столько же возможных Bitcoin-адресов, сколько атомов содержится в Земле. Таким образом сформировать дублирующий адрес (и, таким образом, получить доступ к чьим-то фондам) практически невозможно. Большинство пользователей Bitcoin содержат некоторое число адресов, хранящихся в цифровом кошельке.

Когда кто-то хочет передать какую-то сумму другому человеку, они используют программу, которая реализует транзакцию, содержащую адрес получателя, сумму и криптографические подписи. Эти данные публикуются в P2P-сети, которая проверяет корректность этих данных с помощью общедоступного ключа отправителя, контролирует достаточность суммы на балансе и переадресует всем узлам сети.

Транзакция остается несертифицированной до тех пор, пока она не включена в блок цепочки блоков Bitcoin.

Сегодня имеются в сети тысячи компьютеров, вычисляющих Bitcoin. Каждый компьютер собирает транзакции, посланные широковещательно другими узлами, и пытается найти число, которое решает непредсказуемую криптографическую задачу. Мощный домашний компьютер может испытать сотни миллионов чисел каждую секунду. Чем больше компьютеров занимается такой деятельностью, тем более трудно становится найти решение. Трудность является самонастраиваемой, так что в среднем, новый блок находится каждые 10 минут. Удачливый компьютер, который оказался первым, за каждый блок зарабатывает 50 Bitcoin для своего владельца.

Как только блок найден, он добавляется к бесконечно растущей цепочке блоков (сейчас состоящей из более чем 150,000 блоков). Любая транзакция, занесенная в цепочку блоков, считается корректной, и исключает возможность использование bitcoin для оплаты дважды. Так как единственный способ переписать историю цепочки блоков, это использовать компьютерную мощность, превосходящую ту, что имеет вся сеть Bitcoin, считается, что слишком дорого для одной группы мошенничать таким образом. Сейчас компьютерная мощность сети Bitcoin примерно в 10 раз превосходит по производительности самую большую супер-ЭВМ.

Цепочка блоков позволяет любому клиенту Bitcoin просмотреть всю запись транзакции, чтобы определить баланс счета каждого общедоступного адреса в системе.

Так как вновь созданные Bitcoin постоянно публикуются старателями (miners), можно полагать, что эта валюта является по своей природе инфляционной (с постоянно расширяющейся эмиссией). Это верно для небольших временных интервалов, темп генерации монет устроен так, что каждые четыре года число монет сокращается в два раза. Так как формируется 2.6 млн. Bitcoin каждый год (до января 2013), полное число Bitcoin никогда не будет более 21 млн. И так как Bitcoin являются почти беспредельно делимыми (до 8 десятичных позиций), не следует бояться, что мы не будем иметь достаточно Bitcoin для расширяющихся потребностей экономики.

Система Bitcoin является уникальной, так как она она позволяет безопасно осуществлять расчеты частным лицам, не прибегая к услугам посредников. Bitcoin не могут быть изъяты у их владельца вором, банком или правительством. Никто не может заморозить счет или помешать распоряжаться своими средствами в сети Bitcoin.

Возврат платежа является проблемой для многих продавцов. Виртуально все современные платежные системы (кредитные карты, межбанковские трансферты, PayPal и т.д.) позволяют пользователю отозвать транзакцию, и получить свои деньги назад. Продавцы вынуждены следовать сложной процедуре, чтобы получить свои деньги иногда платя $10-$50 за возврат. Продавцы могут быть вынуждены платить дополнительно до $25,000, если у них используется необычно высокая ставка за возврат.

Продавцы, работающие в реальном времени, в принципе согласны работать с определенным числом ложных возвратов, одновременно расширяя ресурсы компании за счет различных средств детектирования жульнических операций. Пытаясь минимизировать возвраты, продавцы обычно просят своих клиентов раскрыть свои персональные данные, чтобы доставить свои товары или услуги, что приводит к потере конфиденциальности для покупателей.

Транзакции Bitcoin меняют роль доверия, являясь по своей природе безвозвратными. После сертификации в цепочке блоков транзакция практически не может быть обращена вспять. Это дело каждого клиента верить каждому продавцу, у которого они делают заказ. Так как существует много способов установить кредитоспособность продавца (напр., рейтинги реального времени и просто репутация), система доверия Bitcoin хорошо подходит для Интернет-коммерции (верификация кредитоспособности продавцов много проще, чем проверка кредитоспособности всех покупателей).

Из-за того, что Bitcoin не допускает возврата платежа (без согласия продавца), продавцы могут предложить свои продукты более широкой аудитории и требовать меньше индивидуальной информации от своих клиентов.

Политики операторов платежей не всегда хорошо согласованы с теми, кто получает деньги; напр., людьми, которые получают дарения.

Электронная монета определяется как цепочка цифровых подписей. Каждый владелец передает монету следующему, подписывая цифровым способом хэш (SHA-256) предыдущей транзакции и общедоступный ключ следующего владельца, добавляя этот код в конец монеты. Получатель может верифицировать подписи, чтобы проверить цепочку владения.

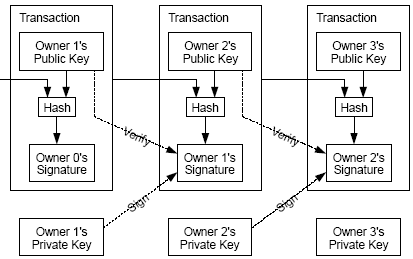
Рис. 1.

Проблема заключается в том, что получатель не может проверить, что один из владельцев не попытался использовать монету дважды. Обычным решением является создание доверительного центра, который проверяет все транзакции, монета должна быть возвращена в такой центр, где будет сформирована новая. После каждой транзакции монета должна быть возвращена в доверительный центр (монетный двор — mint). Только монеты, сформированные монетным двором не будут потрачены дважды. Проблема этого решения заключается в том, что вся платежная система зависит от компании, реализующей функцию монетного двора, так что каждая транзакция должна проходить через нее, как и в случае банка.

Нам нужен способ для каждого получателя платежа получить данные о том, не подписали ли предыдущие владельцы любые более ранние транзакции. Для наших целей имеет значение только самая ранняя транзакция, так что мы не обращаем внимание на более поздние попытки повторной траты денег. Единственный способ подтвердить отсутствие транзакции, это знать обо всех транзакциях. В базовой модели монетного двора, монетный двор отслеживает все транзакции и решает, которая из них была первой. Чтобы выполнить это без арбитра, транзакции должны публично анонсироваться [1], и нам нужна система для участников, чтобы согласовать единую последовательность их получения. Получатель платежа нуждается в доказательстве того, что для времени каждой транзакции большинство узлов согласно с тем, что она была получена первой.

Сервер временных меток

Решение, которое мы предлагаем, начинается с сервера временных меток. Сервер временных меток берет хэш блока элементов, которые нужно привязать по времени и широко публикует хэш, как, например, в постах Usenet [2-5]. Временная метка подтверждает, что данные должны были существовать в определенный момент, чтобы попасть в хэш. Каждая временная метка в своем хэше содержит предыдущую временную метку. Образуется цепочка, где каждая последующая временная метка подтверждает те, что были раньше.

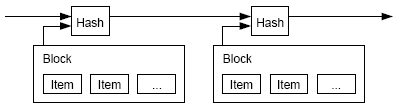
Рис. 2.

Чтобы реализовать распределенный сервер временных меток на базе peer-to-peer, нам будет нужно использовать систему proof-of-work [10] аналогично с Adam Back’s Hashcash [6]. Система proof-of-work использует алгоритм CPP (Client Puzzle Protocol). Система proof-of-work включает в себя поиск кода, который после хэширования, например, посредством SHA-256, имеет некоторого числа нулевых бит. Объем необходимой работы экспоненциально зависит от числа нулевых бит. Хэш легко верифицируется посредством одного хэш-преобразования.

Так как последующие блоки подключаются в цепочку после него, работа по замене блока включает в себя переработку всех последующих блоков.

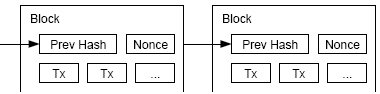
Рис. 3.

Proof-of-work решает в большинстве случаев также проблему репрезентации принятия решения. Если большинство базировалось на схеме один IP-адрес-один-голос, оно может быть свергнуто любым, кто может разместить много IP-адресов. Система Proof-of-work принципиально предполагает схему один-ЦПУ-один-голос. Решение большинства представляется самой длинной цепочкой, на которую потрачено более всего усилий proof-of-work. Если большинство вычислительной мощности контролируется честными узлами, честная цепочка будет рости быстрее, обходя любые конкурирующие цепочки. Чтобы модифицировать последний блок, атакер должен заново проделать proof-of-work блока и всех последующих блоков и затем обойти честные блоки. Мы покажем далее, что вероятность медленного атакера настигнуть остальных при формировании последующих блоков падает экспоненциально.

Рис. 3A. Основная последовательность блоков (чёрные) является самой длинной от начального (зелёный) до текущего. Побочные ветви (cерые) отсекаются. (взято из статьи wipipedia)

Чтобы компенсировать увеличивающееся быстродействие оборудования и вариации заинтересованности рабочих узлов со временем, трудность proof-of-work определяется числом генерируемых блоков в час. Если они генерируются слишком быстро, сложность увеличивается.

Сеть

Сеть работает следующим образом:

1. Новые транзакции широковещательно рассылаются всем узлам.
2. Каждый узел собирает новые транзакции в блок.
3. Каждый узел работает над нахождением proof-of-work для своего блока.
4. Когда узел находит proof-of-work, он широковещательно рассылает блок всем узлам.
5. Узлы воспринимают блок, только если все транзакции в нем корректны и не были уже потрачены.
6. Узлы отмечают восприятиt блока формированием следующего блока в цепочке, используя хэш принятого блока в качестве предыдущего хэша.

Узлы всегда рассматривают самую длинную цепочку, как правильную и будет работать над ее расширением. Если два узла широковещательно рассылают разные версии следующего блока одновременно, некоторые узлы могут получить тот или иной блок первым. В этом случае, они будут работать с блоком, полученным первым, но сохраняют другую ветвь в случае, если она становится длиннее. Проблема разрешается, когда выполняется следующая проверка и одна ветвь становится длиннее. Узлы, которые работают с другой ветвью, переключатся на более длинную ветвь.

Новая транзакция рассылается широковещательно, но необязательно доходит до всех узлов. Широковещательная рассылка блоков устойчива к потерянным сообщениям. Если узел не получил блок, он запросит его, когда он получит следующий блок и поймет, что пропустил один.

Стимул

По определению, первая транзакция в блоке является выделенной, с нее начинается новая монета, принадлежащая создателю блока. Это помогает стимулировать узлы поддерживать сеть, и реализовать способ первичной эмиссии монет в обращение, так как здесь нет единого центра управления для их распространения. Стабильное добавление постоянного числа новых монет аналогично деятельности золотодобытчиков, увеличивающих ресурсы, пуская золото в обращение. В нашем случае расходуется время ЦПУ и электричество.

Стимул может обеспечиваться также за счет транзакционных платежей. Если выходное значение транзакции меньше, чем ее входное значение, разность равна взносу, который добавляется к значению стимула блока, содержащего транзакцию. Если предопределенное число монет поступило в обращение, стимул может полностью преобразоваться в инфляционный взнос.

Стимул может помочь узлам остаться честными. Если алчный атакер способен собрать большую вычислительную мощность, чем все остальные узлы, он может использовать эту возможность для обворовывания людей, забирая свои платежи, либо для генерации новых монет. Он может счесть более выгодным играть по правилам, когда он получает выгоду от формирования большего числа монет, чем все остальные участники вместе взятые, затем подорвать систему и законность своего собственного богатства.

Раз позднейшая транзакция в монете похоронена под достаточным числом блоков, транзакции, потраченныедо этого, могут быть удалены, чтобы сэкономить место на диске. Чтобы облегчить это без разрушения хэша блока, транзакции хэшируются согласно дереву Merkle [7][2][5], с корнем, содержащим хэш блока. Старые блоки могут быть минимизированы путем удаления ветвей дерева. Внутренние хэши запоминать не нужно.

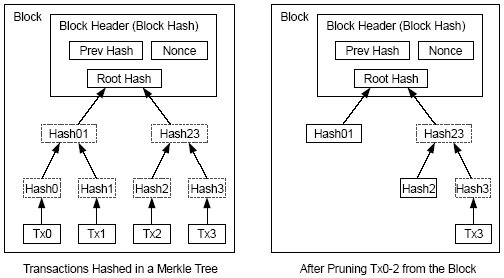
Рис.4.

Заголовок блока без транзакций будет иметь около 80 байт. Если мы предположим, что блоки генерируются каждые 10 минут, 80 байт * 6 * 24 * 365 = 4.2MБ в год. С компьютерной системой, обычно продаваемой с 2ГБ оперативной памяти (2008г), и предсказанием закона Мура роста в 1,2 ГБ в год, память не должна стать проблемой даже, если заголовки блоков должны храниться в памяти.

Упрощенная верификация платежа

Имеется возможность верифицировать платежи без создания сети узлов. Пользователю только нужно иметь копию заголовков блоков самой длинной proof-of-work цепочки, которую он может получить, запрашивая узлы сети пока не убедится в том, что его цепочка длиннее, и получил ветвь Merkle, соединяющую транзакцию с блоком. Он не может проверить транзакцию сам, но связав ее с местом в цепочке, он может понять, что узел сети воспринял ее и блоки, добавленные позднее, подтверждают признание ее сетью.

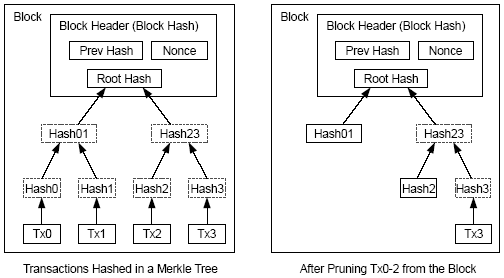
Рис.5.

Как таковая, верификация надежна, пока узлы контролируют сеть, но более уязвима, если сеть подавлена атакером. Пока узлы сети могут верифицировать транзакции сами, упрощенный метод может быть обманут с помощью транзакций сфабрикованных атакером, пока атакер сможет подавлять сеть. Одной из стратегий противодействия может быть прием сигналов тревоги от узлов сети, когда они детектируют некорректные блоки, провоцируя программу пользователя на загрузку полного блока и вызвавшей тревогу транзакции для подтверждения рассогласованности.

Хотя будет возможно работать с монетами индивидуально, будет достаточно трудоемко выполнять отдельную транзакцию для каждого цента в трансферте. Чтобы разрешить суммы делить и объединять, транзакции имеют несколько входов и выходов. Обычно будет существовать либо один вход от большой предыдущей транзакции, либо несколько входов, объединяющих меньшие суммы, и, как правило, два выхода: один для платежа и один для возврата сдачи отправителю, если это требуется.

Следует отметить, что разветвление, где транзакция зависит от нескольких транзакций, и эти транзакции от многих других, не является проблемой. Не существует необходимости извлекать полную копию истории транзакции.

Конфиденциальность

Традиционная банковская модель достигает определенного уровня конфиденциальности, ограничивая доступ к информации для вовлеченных участников и привлекая арбитра. Необходимость анонсировать все транзакции препятствует этому, но конфиденциальность может все же быть реализована путем разрыва информационного потока в другом месте: с помощью анонимности общедоступных ключей. Участники могут видеть, что кто-то пересылает какую-то сумму кому-то, но без персональной привязки транзакции.

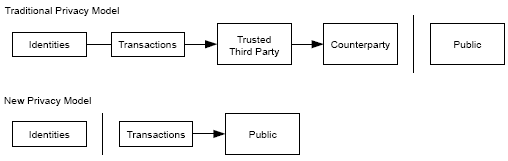
Рис. 6

Новая пара ключей должна использоваться для каждой транзакции, чтобы исключить соединения с общим владельцем. Некоторые соединения все же нельзя избежать в случае многовходовых транзакций, которые в обязательном порядке раскрывают, что их входы принадлежат одному и тому же владельцу. Риск заключается в том, что, если владелец ключа раскрыт, связь раскроет другие транзакции, которые принадлежат тому же владельцу.

Вычисления

Для уменьшения размера БД используется древовидное хэширование. Мы рассматриваем сценарий, когда атакер пытается генерировать альтернативную цепочку быстрее, чем это делается для истинной цепочки. Такая попытка возможна, если атакер пользуется услугами мощной botnet. Даже если это выполнено, это не открывает систему для произвольных изменений, таких как, например, изъятие денег непринадлежащих атакеру. Узлы не воспринимают некорректные транзакции в качестве платежа, и честные узлы никогда не примут блок, их содержащие. Атакер может только попытаться изменить одну из своих собственных транзакций, чтобы вернуть деньги, которые он потратил.

Гонка между честной цепочкой и цепочкой атакера может характеризоваться биномиальным случайным блужданием. Успех в честной цепочке, увеличивающий ее на один блок, увеличивает его перевес на +1 и неудача в цепочке атакера, увеличенная на один блок, уменьшает зазор на -1.

Вероятность того, что атакер сможет нагнать разрыв, аналогична вероятности в задаче разорения игрока Gambler’s Ruin problem. Предположим игрок с неограниченным кредитом начинает, имея долг, и участвует в неограниченном числе попыток, чтобы добиться отыгрыша. Мы можем вычислить вероятность того, что он когда-то отыграется, или того, что атакер сможет сформировать цепочку, длиннее честной, в соответствии с [8]:

p = вероятность нормального узла найти следующий блок
q = вероятность атакеру найти следующий блок
q_z = вероятность того, что атакер сможет догнать, находясь на z блоков позади

В предположении, что p > q, вероятность падает экспоненциально как фунция числа блоков, атакер должен нагонять с ускорением. При шансах против него, если он не сделал рывок раньше, его шансы становятся исчезающе малыми, так как у него практически нет возможности нагнать упущенное.

Рассмотрим, как долго получатель новой транзакции должен ожидать до тех пор пока не будет уверен, что отправитель не может изменить транзакцию. Мы предполагаем, что отправитель — это атакер, который хочет убедить получателя, на некоторое время что он заплатил, затем, спустя некоторое время, перенаправить платеж себе. Получатель поднимет тревогу, когда это случиться, но отправитель надеется, что это случиться слишком поздно.

Получатель генерирует новую пару ключей и передает публичный ключ отправителю незадолго до подписания. Это мешает получателю приготовить цепочку блоков заранее, обрабатывая его непрерывно до тех пор, пока он окажется достаточно впереди, затем сразу исполняет транзакцию. Как только транзакция послана, нечестный отправитель начинает в секрете формировать параллельную цепочку, содержащую альтернативную версию его транзакции.

Получатель ждет, пока транзакция будет добавлена к блоку и z блоков будет присоединены за ним. Он не знает точного числа операций, выполненных атакером, но, предполагая, что честные блоки занимают среднее ожидаемое время на блок, число возможных операций атакера будет иметь распределение Пуассона со средним значением:

λ = zq/p

Чтобы получить вероятность того, что атакер нагонит упущенное, мы умножаем пуассоновскую плотность для каждого приращения, которое он может реализовать на вероятность ликвидации разрыва для данной точки:

Преобразуем, чтобы избежать суммирования бесконечного хвоста распределения…

Преобразуем в C-код…

#include 
double AttackerSuccessProbability(double q, int z)
{
double p = 1.0 - q;
double lambda = z * (q / p);
double sum = 1.0;
int i, k;
for (k = 0; k <= z; k++)
{
double poisson = exp(-lambda);
for (i = 1; i <= k; i++)
poisson *= lambda / i;
sum -= poisson * (1 - pow(q / p, z - k));
}
return sum;
}

Популярность платежной системы Bitcoin растет (см. «3 reasons bitcoins aren’t in your wallet yet«, Zach Miners, December 9, 2013). Но проблемы безопасности ограничивают ее более широкое использование. Банки пока держатся в стороне.

Ссылки

[1] W. Dai, «b-money,» http://www.weidai.com/bmoney.txt, 1998.

[2] H. Massias, X.S. Avila, and J.-J. Quisquater, «Design of a secure timestamping service with minimal trust requirements,» In 20th Symposium on Information Theory in the Benelux, May 1999.

[3] S. Haber, W.S. Stornetta, «How to time-stamp a digital document,» In Journal of Cryptology, vol 3, no 2, pages 99-111, 1991.

[4] D. Bayer, S. Haber, W.S. Stornetta, «Improving the efficiency and reliability of digital time-stamping,» In Sequences II: Methods in Communication, Security and Computer Science, pages 329-334, 1993.

[5] S. Haber, W.S. Stornetta, «Secure names for bit-strings,» In Proceedings of the 4th ACM Conference on Computer and Communications Security, pages 28-35, April 1997.

[6] A. Back, «Hashcash — a denial of service counter-measure,» http://www.hashcash.org/papers/hashcash.pdf, 2002.

[7] R.C. Merkle, «Protocols for public key cryptosystems,» In Proc. 1980 Symposium on Security and Privacy, IEEE Computer Society, pages 122-133, April 1980.

[8] W. Feller, «An introduction to probability theory and its applications,» 1957.

[9] http://ru.wikipedia.org/wiki/Bitcoin

[10] http://en.wikipedia.org/wiki/Proof-of-work_system