Визуальный подход к Крайнестану/Среднестану

Я смотрю на ковер в своем кабинете. Если я буду изучать его через микроскоп, то увижу пересеченную местность. Если я стану разглядывать его через увеличительное стекло, то местность покажется мне более ровной, но все же весьма ухабистой. Но когда я смотрю на него с высоты своего роста, он выглядит почти таким же гладким, как лист бумаги. Ковер, обозреваемый невооруженным глазом, соответствует Среднестану и закону больших чисел: я вижу сумму волнистостей, которые сглаживаются. Это как гауссова случайность: моя чашка с кофе не подпрыгивает на столе, потому что суммарное движение всех ее частиц оборачивается стабильностью. Таким же образом, суммируя маленькие гауссовы неопределенности, получаешь определенность: это закон больших чисел.

Гауссиана не самоподобна, и поэтому моя кофейная чашка не прыгает.

Рассмотрим теперь прогулку в горы. Как высоко ни поднимешься над поверхностью земли, она будет оставаться неровной. Даже при взгляде с высоты 30 ооо футов. Когда летишь над Альпами, вместо маленьких камешков видишь зазубренные вершины. Значит, некоторые поверхности — не из области Среднестана и изменение масштаба не приводит к их сглаживанию. (Заметим, что эффект выравнивания достигается, только если подняться на еще большую высоту. Наша планета представляется гладким шаром тем, кто наблюдает за ней из космоса, но это потому, что она слишком маленькая. Будь Земля крупнее, на ней нашлись бы горы, превосходящие по высоте Гималаи, и потребовалась бы еще большая удаленность от нее, чтобы их очертания стерлись. Точно так же, живи на Земле больше людей, пусть даже с тем же средним достатком, наверняка нашелся бы кто-то, чей капитал перекрыл бы состояние Билла Гейтса.)

Рисунки и и 12 иллюстрируют эту идею: глядя на первый рисунок, можно подумать, что на землю упала крышка от объектива.

Вернемся к нашему краткому упоминанию побережья Британии. Если взглянуть на него с самолета, контуры не будут так уж отличаться от контуров, видимых с ближайшего обрыва. Изменение масштаба не меняет формы или степени гладкости.

Бисер перед свиньями

Но какое отношение фрактальная геометрия имеет к распределению капитала, величине городов, обороту финансовых рынков, потерям на войне или размеру планет? Давайте соединим точки.

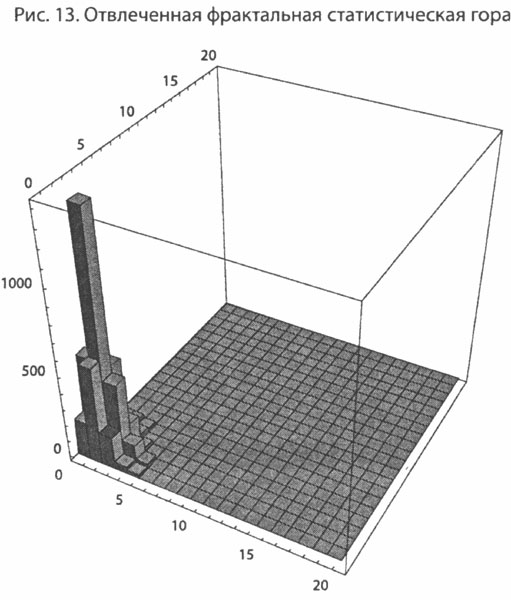
Ключ здесь в том, что у фрактала есть числовая, или статистическая, размерность, которая (более или менее) сохраняется при изменении масштаба, — пропорции (в отличие от гауссианы) постоянны. Другой пример такого самоподобия представлен на рисунке 13. Как мы знаем из главы 15, сверхбогатые сходны с богатыми, только богаче, — богатство масштабно-независимо, или, вернее, о его зависимости ничего не известно.

В 1960-е годы Мандельброт изложил свои идеи о ценах на предметы потребления и акции экономической элите, и экономисты-финансисты пришли в восторг. В 1963 году тогдашний декан бизнес-магистратуры университета Чикаго Джордж Шульц предложил ему место профессора. Это тот самый Джордж Шульц, который позже стал госсекретарем Рональда Рейгана.

Через некоторое время Шульц позвонил ему, чтобы отказаться от своего предложения.

Сейчас, через сорок четыре года, в экономике и социальной статистике ничего не изменилось, если не считать некоторых косметических поправок, учитывающих присутствие в мире лишь рядовой случайности, — и при этом нобелевские медали раздаются направо-налево. Появилось несколько статей с «доказательствами» неправоты Мандельброта, авторы которых не понимают того, о чем постоянно твержу я: выискивая периоды, лишенные редких событий, всегда можно получить данные, «подтверждающие», что стоящий за ними процесс — из разряда гауссовых. Точно так же можно выбрать день, в который не произошло убийств, и использовать его как «свидетельство» нашей безгрешности. Я повторю, что из-за асимметрии, свойственной индукции, проще оспорить невиновность, чем признать ее, и по той же причине проще оспорить гауссиану, чем принять. Фрактал же, напротив, труднее оспорить, чем принять. Почему? Потому что одно-единственное событие может опровергнуть утверждение, что перед нами — гауссиана.

В итоге четыре десятилетия тому назад Мандельброт вручил экономистам и пекущимся о своем резюме филистерам жемчуг, который они отвергли, потому что его идеи были для них слишком хороши. Именно это самое и называют margaritas ante porcos — бисер перед свиньями.

В оставшейся части главы я расскажу, почему для объяснения большой доли случайностей мною предлагаются именно мандельбротовы фракталы, не обязательно в их точном употреблении. Фракталы — это вариант по умолчанию, приближение, основа. Они не решают проблему Черного лебедя и не превращают всех Черных лебедей в явления предсказуемые, но они значительно смягчают проблему Черного лебедя, делая эпохальные события постижимыми. (Черные лебеди становятся Серыми. Почему Серыми? Потому что чистая белизна есть только в гауссиане. Подробности позже.)

Логика фрактальной случайности (с предупреждением)[77]

Я показал в таблицах возрастания богатства в главе 15 логику фрактального распределения: если богатство удваивается с 1 (минимум) до 2 (минимум) миллионов, доля людей с таким капиталом урезается вчетверо, то есть налицо экспонента 2. При экспоненте 1 доля такого же богатства уменьшилась бы вдвое. Экспонента — это показатель степени, поэтому широко распространен термин степенной закон. Будем называть количество случаев, перекрывающих некий уровень, превышением: превышение 2 миллионов — это количество людей с состоянием больше 2 миллионов. Одно из основных свойств этих фракталов (или еще один способ выразить их основное свойство — масштабируемость) заключается в том, что отношение двух превышений будет отношением их нижних порогов[78], возведенным в степень, равную минус экспоненте.

Проиллюстрируем это. Положим, вы «думаете», что только 96 названий книг в год разойдутся тиражом более 250 000 экземпляров (как это было в прошлом году), и, «по-вашему», экспонента должна быть примерно 1,5. Простым умножением 96 на (500 000 / 250 000)-1,5 вы можете определить, что примерно 34 названия разойдутся тиражом более 500 000 экземпляров. Пойдя далее, мы установим, что около 8 книг будут проданы в количестве более миллиона экземпляров: 96 х (1 000 000 / 250 000)-1,5.

В итоге четыре десятилетия тому назад Мандельброт вручил экономистам и пекущимся о своем резюме филистерам жемчуг, который они отвергли, потому что его идеи были для них слишком хороши. Именно это самое и называют margaritas ante porcos — бисер перед свиньями.

В оставшейся части главы я расскажу, почему для объяснения большой доли случайностей мною предлагаются именно мандельбротовы фракталы, не обязательно в их точном употреблении. Фракталы — это вариант по умолчанию, приближение, основа. Они не решают проблему Черного лебедя и не превращают всех Черных лебедей в явления предсказуемые, но они значительно смягчают проблему Черного лебедя, делая эпохальные события постижимыми. (Черные лебеди становятся Серыми. Почему Серыми? Потому что чистая белизна есть только в гауссиане. Подробности позже.)

В итоге четыре десятилетия тому назад Мандельброт вручил экономистам и пекущимся о своем резюме филистерам жемчуг, который они отвергли, потому что его идеи были для них слишком хороши. Именно это самое и называют margaritas ante porcos — бисер перед свиньями.

В оставшейся части главы я расскажу, почему для объяснения большой доли случайностей мною предлагаются именно мандельбротовы фракталы, не обязательно в их точном употреблении. Фракталы — это вариант по умолчанию, приближение, основа. Они не решают проблему Черного лебедя и не превращают всех Черных лебедей в явления предсказуемые, но они значительно смягчают проблему Черного лебедя, делая эпохальные события постижимыми. (Черные лебеди становятся Серыми. Почему Серыми? Потому что чистая белизна есть только в гауссиане. Подробности позже.)

Логика фрактальной случайности (с предупреждением)[77]

Я показал в таблицах возрастания богатства в главе 15 логику фрактального распределения: если богатство удваивается с 1 (минимум) до 2 (минимум) миллионов, доля людей с таким капиталом урезается вчетверо, то есть налицо экспонента 2. При экспоненте 1 доля такого же богатства уменьшилась бы вдвое. Экспонента — это показатель степени, поэтому широко распространен термин степенной закон. Будем называть количество случаев, перекрывающих некий уровень, превышением: превышение 2 миллионов — это количество людей с состоянием больше 2 миллионов. Одно из основных свойств этих фракталов (или еще один способ выразить их основное свойство — масштабируемость) заключается в том, что отношение двух превышений будет отношением их нижних порогов[78], возведенным в степень, равную минус экспоненте.

Проиллюстрируем это. Положим, вы «думаете», что только 96 названий книг в год разойдутся тиражом более 250 000 экземпляров (как это было в прошлом году), и, «по-вашему», экспонента должна быть примерно 1,5. Простым умножением 96 на (500 000 / 250 000)-1,5 вы можете определить, что примерно 34 названия разойдутся тиражом более 500 000 экземпляров. Пойдя далее, мы установим, что около 8 книг будут проданы в количестве более миллиона экземпляров: 96 х (1 000 000 / 250 000)-1,5.

Давайте рассмотрим разные выверенные экспоненты для всевозможных явлений.

Но прежде всего следует предупредить, что эти экспоненты ни в коем случае не точные показатели. Почему, мы увидим через минуту, но пока отметим, что этих параметров мы не наблюдаем; мы их просто угадываем или вводим для статистики, и поэтому временами бывает трудно узнать истинные параметры — если они вообще существуют. Сначала поговорим о практической роли экспоненты.

Таблица 3 иллюстрирует влияние крайне невероятного. Она показывает долю верхнего 1 процента и верхних 20 процентов в общей сумме. Чем меньше экспонента, тем выше эта доля. Но посмотрите, сколь чувствителен процесс: переход от 1,1 к 1,3 разом уменьшает процент с 66 до 34. Разница в экспоненте всего лишь в 0,2 резко меняет результат — и ведь такую разницу способна дать простая ошибка в расчетах. А разница-то принципиальная: только подумайте, что мы точно не знаем, чему равен показатель, потому что не можем измерить его непосредственно. Единственное, что нам остается, — это делать прикидки, основываясь на прошлых данных, или полагаться на теории, которые позволяют построить некую модель, которая, в свою очередь, позволяет строить некие предположения. Но у таких моделей могут оказаться скрытые изъяны, из-за чего опасно безоговорочно применить их к реальности.

Итак, помните, что экспонента 1,5 — это приближение, что ее трудно вычислить, что она не свалится на вас с неба, по крайней мере на счет раз-два, и что вы столкнетесь с гигантской погрешностью. Вы обнаружите, что число книг, проданных в количестве более чем миллион экземпляров, не обязательно будет равно 8 — их может быть целых 20 или всего лишь 2.

Еще важнее то, что применение именно этой экспоненты допустимо начиная с некоторого числа, называемого «переходным». Это могут быть 200 000 книжных экземпляров, а то и 400 000. Точно так же у богатства, скажем, выше 600 миллионов долларов, когда неравенство растет, и ниже этой черты — свойства разные. Как узнать, где точка перехода? Это проблема. Мои коллеги и я обработали примерно 20 миллионов финансовых данных. Набор данных у нас у всех был один, но мы так и не пришли к согласию в том, какова должна быть экспонента. Мы понимали, что данные подчинены действию фрактального степенного закона, но, как оказалось, точное число высчитать невозможно. Однако знание того, что распределение масштабируемо и фрактально, давало нам право действовать и принимать решения.

Проблема верхней границы

Некоторые аналитики исследовали и согласились принять фрактал — «до определенного предела». Они утверждают, что богатство, продаваемость книг и рыночные обороты на некотором уровне перестают быть фрактальными. Предлагаемый ими метод — «усечение»- Я согласен, что есть уровень, на котором фрактальность может сойти на нет, только вот где он? Сказать: я не знаю, где находится верхний предел, и сказать: предела нет — на практике одно и то же. Устанавливать верхний предел крайне опасно. Кто-нибудь может предложить: ограничим наш анализ богатства потолком в 150 миллиардов долларов. Но кто-то другой имеет все основания возразить: а почему не 151 миллиард? Или не 152? С таким же успехом можно считать, что эта переменная стремится к бесконечности.

Не верьте в точность

Я научился на опыте нескольким трюкам: какую бы экспоненту я ни пытался высчитать, она, скорее всего, будет преувеличена (напомню, что чем больше экспонента, тем скромнее роль значительных отклонений) — то, что у вас перед глазами, оказывается менее «чернолебяжьим», чем то, что от вас скрыто. Я называю это проблемой маскарада.

Скажем, я генерирую процесс с экспонентой 1,7. Вы не видите работы генерирующего устройства, а только ряд полученных данных. Если я спрошу, какова экспонента, вы с большой долей вероятности остановитесь на чем-то вроде 2,4. Итог будет таким даже при миллионе показателей. Причина в том, что некоторым фрактальным процессам нужно очень много времени, чтобы раскрыть свои свойства, и вы недооцениваете силу вероятного всплеска.

Иногда фрактал может умело замаскироваться под гауссиану, особенно когда «разветвление» начинается с большого числа. У фрактальных распределений всплески такого рода настолько редки, что мы теряем бдительность: мы не распознаем их фрактальную структуру.

Снова о лужице

Из всего вышесказанного вы уже наверняка поняли, что, какую бы модель мы ни признавали властительницей мира, узнать ее параметры непросто. Так что в связи с Крайнестаном вновь встает проблема индукции, на сей раз еще более остро, чем в любой из предыдущих глав. Говоря по-простому, если процесс имеет фрактальный характер, он оперирует громадными величинами, а значит, есть вероятность громадных отклонений, но насколько часто эти отклонения будут возникать, трудно сказать мало-мальски уверенно. Это напоминает проблему лужицы: она могла образоваться из самых разных кубиков льда. Как человек, который идет от реальности к возможным объясняющим моделям, я встречаюсь с массой проблем совершенно иного свойства, чем проблемы тех, кто поступает наоборот.

Я только что прочел три «научно-популярные» книги, посвященные исследованиям сложных систем: «Вездесущесть» Марка Бьюкенена, «Критическую массу» Филипа Болла [79] и «Почему мало что удается» Пола Ормерода. По мнению этих трех авторов, мир социальных наук полон степенных законов, и с таким взглядом я конечно же согласен. Они также заявляют, что многие из явлений такого порядка на самом деле универсальны, что есть удивительное сходство между разными процессами в природе и поведением социальных групп, с чем я тоже согласен. Подкрепляя свои исследования теориями различных сетей, они указывают на поразительное соответствие между так называемыми критическими явлениями в естественных науках и самоорганизацией социальных групп. Они объединяют процессы, порождающие лавины, социальные поветрия и «информационные каскады», с чем я опять же согласен.

Универсальность — одна из причин, по которым степенные законы, связанные с критическими точками, особенно интересуют физиков. Есть много ситуаций как в теории динамических систем, так и в статистической механике, когда многие свойства динамики возле критической точки не зависят от особенностей действующей динамической системы. Экспонента в критической точке может быть одинаковой для многих систем одной группы, даже если во многом другом системы различны. Я почти согласен с такой трактовкой универсальности. Наконец, все три автора призывают нас применять методы статистической физики, сторонясь эконометрики и гауссоподобных немасштабируемых распределений, как разносчиков чумы, в чем я с ними полностью солидарен.

Но все три автора, добиваясь точности или призывая к ней, допускают просчет, смешивая прямые и обратные процессы (задачу и обратную задачу), — что для меня есть величайший научный и эпистемологический грех. Они неодиноки в этом; почти каждый, кто работает с данными, но не принимает решений на основе этих данных, подвержен тому же греху, разновидности искажения нарратива. В отсутствие обратной связи ты смотришь на модели и думаешь, что они подтверждают реальность. Я верю в идеи этих трех книг, но не в способ их применения — и уж конечно не в точность, которую авторы им приписывают. На самом деле теория сложности должна учить нас подозрительнее относиться к научным разработкам «точных» моделей реальности. Она не делает всех лебедей белыми, это ясно; она делает их Серыми, и только.

Как я сказал раньше, мир для глядящего «снизу вверх» эмпирика с эпистемологической точки зрения — буквально мир иной. Мы лишены роскоши сидеть и медитировать над уравнением, правящим Вселенной; мы только наблюдаем данные, выдвигаем предположения о том, каким может быть процесс в действительности, и «калибруем» их, подправляя наше уравнение в соответствии с дополнительной информацией. По мере того как события разворачиваются перед нами, мы сравниваем то, что видим, с тем, что ожидали увидеть. Обычно открытие того факта, что история движется вперед, а не назад, сбивает с людей спесь, особенно с тех, кто знаком с искажением нарратива. Какими бы самонадеянными ни были бизнесмены, их часто приводят в чувство напоминания о разрыве между задумкой и результатом, между точными моделями и реальностью.

То, о чем я говорю, — это непроницаемость, неполнота информации, невозможность увидеть «генератор мира». История не открывает нам своих мыслей — мы должны их угадывать.

От представления к реальности

Вышеизложенная идея связывает все части книги. Многие изучают психологию, математику или теорию эволюции и потом пытаются выжать из них капитал, применяя свои знания в бизнесе. Я же предлагаю как раз противоположное: изучайте неистовую, незапротоколированную, отрезвляющую неопределенность рынка, чтобы вам приоткрылась природа случайности, которая дает ключ к психологии, теории вероятности, математике, теории решений и даже статистической физике. Вы увидите коварные проявления игровой ошибки, искажения нарратива, великого заблуждения платонизма, идущего от представления к реальности.

Впервые встретив Мандельброта, я полюбопытствовал, почему он, признанный ученый, которому уж наверно есть чем заняться в жизни, заинтересовался таким низменным предметом, как финансы. Ведь финансы, экономика, по моим представлениям, — это такая сфера, где набираются опыта, наблюдая разные эмпирические явления, и пополняют свой банковский счет деньгами, прежде чем заняться чем-то большим и лучшим, послав «в ж… деньги». Ответ Мандельброта гласил: «Данные, золотая жила данных!» В самом деле, все забывают, что, прежде чем перейти к физике и геометрии природы, он начинал в экономике. Работа с таким изобилием данных сбивает с нас спесь; она вооружает нас интуитивным пониманием того, в каком направлении нужно совершать путь между представлением и реальностью.

Проблема зацикленности статистики (которую также можно назвать статистическим порочным кругом) состоит в следующем. Скажем, вам нужны прошлые данные, чтобы определить, является ли распределение вероятности нормальным, фрактальным или каким-то еще. Нужно установить, достаточно ли у вас данных, чтобы ваше утверждение было обоснованным. Как узнать, достаточно ли у нас данных? Из распределении вероятности. Оно покажет, хватает ли у тебя данных, чтобы то, что ты предполагаешь, «заслуживало доверия». Для кривой нормального распределения достаточно малого количества точек (опять закон больших чисел). А как узнать, что распределение нормальное? Вообще-то на основании данных. Итак, нам нужны данные, чтобы узнать, каково распределение вероятности, и распределение вероятности, чтобы узнать, сколько данных нам нужно. Это порочный крут.

Такого круга не возникает, если предположить заранее, что распределение нормальное. По определенной причине свойства нормального распределения довольно легко выявляются. В отличие от тех, что присущи распределению в Крайнестане. Поэтому выбор гауссианы для выве дения некоего общего закона очень удобен мы используем его по умолчанию именно по этой причине. Я не устаю повторять, что априорная ставка на гауссиану допустима лишь в небольшом числе областей, таких как статистика преступности, уровни смертности, вопросы из Среднестана. Но только не там, где дело касается исторических данных с неизвестными свойствами и крайнестанских вопросов.

Но почему статистики, работающие с историческими данными, закрывают на это глаза? Во-первых, им не хочется признавать, что вся их деятельность перечеркивается проблемой индукции. Во-вторых, они не несут никакой ответственности за результаты своих предсказаний. Соревнование, устроенное Макридакисом, показало нам, что они во власти искажения нарратива и не хотят этого знать.

Еще раз: опасайтесь предсказателей

Поднимем проблему на уровень выше. Как я заметил ранее, существует много модных моделей, пытающихся объяснить происхождение Крайнестана. Вообще-то они группируются в два широких класса, но встречаются и другие подходы. Первый класс — это простые модели типа «деньги идут к деньгам» (или «успех тянет за собой успех»), объясняющие скопление людей в городах, доминирование на рынке компании «Майкрософт» (а не «Эппл») и формата VHS (а не Betamax), создание академических репутаций и т.д. Второй класс включает в себя так называемые «модели просачивания», в центре внимания которых — не поведение индивида, а среда его обитания. Когда льешь воду на пористую поверхность, структура поверхности оказывается важнее, чем свойства жидкости. Когда песчинка ударяется о кучу других песчинок, именно характер местности определяет, сойдет ли лавина.

Почти все модели, разумеется, претендуют на прогностическую точность, и это меня бесит. Они — хорошие инструменты для иллюстрации происхождения Крайнестана, но я настаиваю на том, что «генератор реальности» не подчинен им настолько, чтобы с их помощью можно было делать точные прогнозы. Все, что я нахожу в современной литературе на тему Крайнестана, свидетельствует именно об этом. Перед нами здесь снова встает серьезнейшая проблема калибровки, так что лучше бы нам избежать обычных ошибок, совершаемых при калибровке нелинейного процесса. Напомним, что у таких процессов больше степеней свободы, чем у линейных (как мы показали в главе и), а следовательно, чрезвычайно велик риск того, что модель окажется неправильной. Мне то и дело попадают в руки книги или статьи, которые ратуют за применение моделей статистической физики к реальности. Например, восхитительные книги Филипа Болла насыщены информацией и иллюстративным материалом, но это не основа для точных количественных моделей. Не встречайте их по одежке.

Однако посмотрим, что мы можем позаимствовать у этих моделей.

Снова счастливое решение

Во-первых, признавая масштабируемость, я соглашаюсь с тем, что любое самое большое число возможно. Другими словами, неравенство не должно прекращаться после достижения некоторой известной верхней границы.

Скажем, продано около 60 миллионов экземпляров книги «Код да Винчи». (Библии продано около миллиарда экземпляров, но вынесем ее за скобки, ограничившись светскими книгами, написанными отдельными авторами.) Хотя мы и не встречали светских книг, разошедшихся тиражом 200 миллионов экземпляров, можно считать, что вероятность этого не нулевая. Да, она мала, но не нулевая. На каждые три бестселлера в духе «Кода да Винчи» может найтись один супербестселлер, и, хотя до сих пор таких не появилось, исключить этого нельзя. А на каждые пятнадцать «Кодов да Винчи» — супербестселлер, который разойдется, например, тиражом 500 миллионов экземпляров.

Применим ту же логику к богатству. Допустим, самый богатый человек на Земле имеет капитал размером 50 миллиардов долларов. Есть вероятность, которой нельзя пренебречь, что в следующем году из ниоткуда выскочит кто-то, кто имеет 100 или более миллиардов. На каждых трех людей, имеющих более чем 50 миллиардов долларов, может найтись один со 100 миллиардами. Есть вероятность, хоть и гораздо меньшая, что найдется кто-то, владеющий более чем 200 миллиардов долларов — одна треть предыдущей вероятности, но все равно не нуль. Есть даже крошечная, но не нулевая вероятность того, что обнаружится кто-то, чье состояние превышает 500 миллиардов долларов.

Это подсказывает мне следующее: я могу строить предположения о вещах, существование которых свидетельствами не подтверждается, но они должны принадлежать царству возможного. Где-то там есть бестселлер, о каких прежде не слыхивали, но его следует принимать во внимание. Напомню основную мысль главы 13: благодаря этому отсутствию предела вложение денег в книгу или лекарство порой оказывается более выгодным, чем подсказывают статистика или прежние наблюдения. Но из-за него же потери на фондовом рынке часто превосходят те, что когда-либо имели место.

Войны фрактальны по своей природе. Война, которая убьет больше людей, чем опустошительная Вторая мировая, возможна. Она маловероятна, но не исключена, хотя такой войны никогда не случалось в прошлом.

Во-вторых, чтобы прояснить вопрос о точности, я приведу пример из природы. Гора чем-то похожа на камень, она сродни камню, у нее есть семейное сходство с камнем, но это не одно и то же. Для описания такого сходства есть замечательное слово — самоподобный, а уж никак не самоповторяющийся, но Мандельброт не потрудился тщательно разжевать то, что вкладывается им в понятие «подобие», и в обиход вошел термин «самоповторение», подразумевающий точное, а не семейное сходство. Как в случае с горой и камнем, распределение состояния выше миллиарда долларов не совсем таково, как распределение состояния менее миллиарда долларов, но эти распределения «подобны».

В-третьих, как я сказал раньше, в области эконофизики (являющейся приложением статистической физики к социальным и экономическим явлениям) было много статей, в которых предпринималась попытка такой «градуировки», то есть извлечения чисел из мира явлений. Многие порываются предсказывать. Увы, мы не способны предсказать «марш-бросок» к кризису или поветрию. Мой друг Дидье Сорнетт пробует строить прогностические модели, которые я обожаю, хотя и не могу использовать для прогнозирования, — только, пожалуйста, не говорите ему об этом: вдруг он перестанет их строить. То, что я не могу использовать их так, как предполагает он, не лишает смысла его работу (не имеющую ничего общего с традиционной экономикой, чьи модели ошибочны в корне), а просто требует незашоренного мышления для ее интерпретации. С некоторыми из сорнеттовских феноменов мы, может, еще сумеем поладить — но не со всеми.

Вся эта книга посвящена Черному лебедю. Это не потому, что я влюблен в него; как гуманист, я его ненавижу. Я виню его во многих несправедливостях и бедах. Поэтому я хотел бы устранить многих Черных лебедей или хотя бы смягчить последствия их воздействия и защититься от них. Познание фрактальной случайности — это способ приготовиться к сюрпризу, превратить некоторых лебедей в ожидаемых, осознать, чем они чреваты, малость их, так сказать, «осветлить». Но фрактальная случайность не дает точных ответов. Преимущества здесь следующие. Если ты знаешь, что фондовый рынок может обвалиться, как и было в 1987 году, то это событие не Черный лебедь. Обвал 1987 года — не есть нечто, выходящее из ряда вон, если пользоваться фракталом с экспонентой 3. Если знать, что биотехнологические компании могут создать для нас супермегалекарство, которое окажется популярнее, чем все, какие у нас были прежде, то оно не будет Черным лебедем и вы не удивитесь, если оно появится.

Итак, фракталы Мандельброта позволяют нам держать под контролем Черных лебедей, но не всех. Я сказал выше, что некоторые Черные лебеди появляются потому, что мы пренебрегаем источниками случайности. Другие возникают, когда мы преувеличиваем экспоненту фрактала. Серый лебедь принадлежит к разряду моделируемых экстремальных ситуаций, Черный лебедь — это нечто из области «неизвестного неизвестного».

Я сел и обсудил вышеизложенное с великим человеком, и это обсуждение превратилось, как обычно, в языковую игру. В главе 9 я объяснил различие, которое экономисты делают между «неопределенностью по Найту» (которую просчитать нельзя) и «риском по Найту» (который просчитать можно). Это различие не настолько оригинальная идея, чтобы не было слова для ее выражения, так что мы поискали его во французском языке. Мандельброт упомянул одного из своих друзей — аристократа-математика Марселя-Поля Шютценберже, утонченного эрудита, которому (как и автору этой книги) все быстро приедалось: дальше точки «убывающей отдачи» он никогда в своих работах не шел. Шютценберже настаивал на отчетливом различии во французском языке между «hasard» и «fortuit». «Hasard», от арабского «az-zahr», означает (как и «alea», игральные кости) контролируемую случайность; «fortuit» — это мой Черный лебедь, то, что абсолютно непредсказуемо. Мы обратились за помощью к словарю «Малый Робер» и убедились в правоте математика. «Fortuit», похоже, соответствует моей эпистемической непроницаемости, l’imprevu et поп quantifiable [80] ; «hasard» — более игровому виду неопределенности, описанному шевалье де Мере [81] , одним из ранних теоретиков азартных игр. Стоит заметить, что те же арабы, возможно, ввели еще одно слово, имеющее отношение к неопределенности, — «rizk», что значит собственность.

Я повторю: Мандельброт занимается Серыми лебедями, я занимаюсь Черным лебедем. Мандельброт одомашнил многих моих Черных лебедей, но не всех и не полностью. Однако с помощью своего метода он дает нам проблеск надежды, способ задуматься о проблемах неопределенности. Ведь гораздо безопаснее знать, где находятся дикие животные.

Глава 17. Безумцы Локка, или «Гауссовы кривые» не к месту [82]

Что? — Любой может стать президентом. — Наследие Альфреда Нобеля. — Те средневековые дни.

В моем доме два кабинета: один настоящий, с интересными книгами и рукописями, другой — нелитературный, где я не люблю работать, куда я ссылаю дела прозаические и узконаправленные. В нелитературном кабинете есть стена, уставленная книгами по статистике и истории статистики, книгами, которые мне никогда не хватало силы духа сжечь или выбросить, хотя я считаю их абсолютно бесполезными для чего-либо, кроме академических выкладок (Карнеад, Цицерон и Фуше могут сказать о вероятности гораздо больше, чем все эти псевдоинтеллектуальные тома). Я не могу использовать их в аудиториях, потому что обещал себе никогда никому не пудрить мозги, даже если буду умирать с голода. Почему же я не могу использовать их? Потому что ни одна из этих книг не имеет отношения к Крайнестану. Ни одна. Те немногие, что все-таки имеют, написаны не статистиками, а статистическими физиками. Мы учим людей методам Среднестана и выпускаем их в Крайнестан. Это все равно что прописывать людям лекарства, предназначенные для растений. Неудивительно, что мы подвергаемся колоссальному риску: обращаемся с крайнестанскими реалити как со среднестанскими и называем это «приближением».

Несколько сотен тысяч студентов в бизнес-школах и на факультетах социологии от Сингапура до Урбана-Шампейна (штат Иллинойс), как и люди в деловом мире, продолжают изучать «научные» методы, которые сплошь основаны на гауссиане, сплошь построены на игровой ошибке.

В этой главе рассматриваются бедствия, происходящие от приложения липовой математики к социологии. А ее основную тему можно сформулировать так: «Как вредит нашему обществу Шведская академия, вручая Нобелевскую премию».

Только пятьдесят лет

Вернемся к истории моей деловой жизни. Посмотрите на график на рисунке 14. За последние пятьдесят лет десять самых выдающихся дней на финансовых рынках принесли половину прибыли. Десять дней из пятидесяти лет. Все остальное время мы потратили на пустяки.

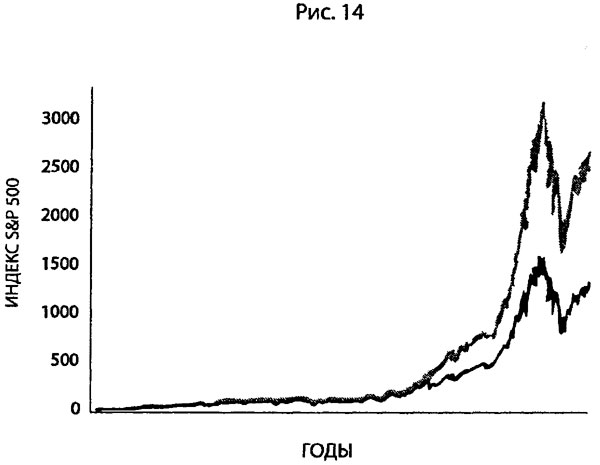
Так что любому, кого резкий подскок на шесть сигм не убеждает в принадлежности рынков к Крайнестану, надо проверить, все ли у него в порядке с головой. Во множестве статей показывается неадекватность гауссова семейства распределений и масштабируемая природа рынков. Напомню, что за годы работы я сам прогнал взад-вперед через статистические модели 20 миллионов данных. Именно это заставило меня презирать всех, кто говорит о рынках в терминах гауссианы. Но человеку трудно бывает смириться с последствиями масштабируемости.

Самое странное то, что деловые люди обычно соглашаются, когда говорят со мной или слушают, как я излагаю свои взгляды. Но стоит этим же людям на следующий день прийти в офис, как они возвращаются к своим привычным гауссовым инструментам. Их мышление «ареал-специфично»: на конференции они способны мыслить критически, а в офисе — нет. К тому же гауссовы инструменты дают им цифры, что вроде бы «лучше, чем ничего». Исчисленная мера будущей неопределенности отвечает нашему глубинному желанию упрощать, даже если это означает втискивать в одно-единственное число материи слишком разнородные, чтобы их можно было характеризовать подобным образом.

Предательство клерков

Я завершил главу 1 во время обвала фондового рынка в 1987 году, который позволил мне активно пропагандировать свою идею Черного лебедя. Сразу после обвала, когда я во всеуслышание объявил шарлатанами тех, кто пользуется сигмой (то есть стандартным отклонением) как мерой степени риска и случайности, со мной все согласились. Если бы мир финансов подчинялся гауссовому распределению, такой эпизод, как обвал (более двадцати стандартных отклонений), происходил бы не чаще, чем раз в несколько миллиардов жизней Вселенной (см. пример с ростом в главе 15). В обстоятельствах 1987 года все признали, что редкие события случаются и что они — главный источник неопределенности. Однако никто не захотел отказаться от гауссианы как основного измерительного инструмента — «ведь другого-то у нас нет!». Всем требуется привязка в виде числа. Но два метода логически несовместимы.

Хотя я и не знал об этом, в 1987 году не в первый раз выяснилось, что идея гауссианы — безумие. Мандельброт еще году эдак в 1960-м познакомил экономический истеблишмент с масштабируемостью и показал несоответствие «гауссовой кривой» тогдашним ценам. Но, после того как прошел восторг, финансисты поняли, что им придется заново учиться своему ремеслу. Один из влиятельных экономистов того времени, покойный Пол Кутнер, писал: «Мандельброт, как ранее премьер-министр Черчилль, обещал нам не утопию, но кровь, пот, труд и слезы [83] . Если он прав, то почти все наши статистические инструменты устарели [или] бессмысленны». Я предлагаю две поправки к утверждению Кутнера. Во-первых, я заменил бы «почти все» на «все». Во-вторых, я не согласен со всякими там «потом и кровью». Я считаю, что случайность Мандельброта понять значительно легче, чем обычную статистику. Просто, входя в эту область, не полагайтесь на устаревшие теоретические инструменты и не ожидайте большой определенности.

Любой может стать президентом

А теперь — краткая история Нобелевской премии по экономике. Шведский государственный банк учредил ее в честь Альфреда Нобеля, не прислушавшись к мнению его родных, которые хотят, чтобы ее отменили, так как полагают, что Нобель переворачивается в гробу от отвращения. Один активист из числа родственников Нобеля называет премию пиар-ходом экономистов, желающих вознести свою область на более высокую ступень пьедестала, чем та, которой она заслуживает. Конечно, премию получили некоторые значительные мыслители, такие как психолог-эмпирик Дэниел Канеман и здравомыслящий экономист Фридрих Хайек. Но у комитета вошло в привычку выдавать премии памяти Нобеля тем, кто «упорядочивает» процесс при помощи псевдонауки и жульнической математики. После обвала фондового рынка они наградили двух теоретиков, Гарри Марковича и Уильяма Шарпа, которые прекрасно строили платоновские модели на гауссовой основе, внося вклад в то, что называется современной портфельной теорией. Если принять за исходное не гауссиану, а масштабируемость цен, от их умопостроений останется один пшик. Нобелевский комитет мог бы проверить модели Шарпа и Марковича — они работают как снадобья знахарей, продающиеся через интернет, — но, кажется, никто в Стокгольме об этом не подумал. Не соблаговолил комитет обратиться и к нам, практикам, чтобы узнать наше мнение; вместо этого он положился на оценки академических кругов, которые в некоторых дисциплинах бывают насквозь коррумпированы. После этой премии я сделал предсказание: «В мире, где эти двое получают нобелевку, может случиться что угодно. Любой может стать президентом».

Таким образом, Шведский государственный банк и Нобелевский комитет несут значительную долю ответственности за распространение современной гауссовой портфельной теории, которую разные конторы сумели ловко употребить для прикрытия своих тылов. Продавцы программного обеспечения заработали миллионы долларов на сбыте «увенчанных Нобелем» методов. Кто может обвинить вас в неправоте, если вы их используете? Как ни странно, в деловом мире каждый с самого начала знал, что сама эта идея — обман, но к подобным методикам привыкли. Ален Гринспен, председатель Федерального резервного банка США, вроде бы сказал однажды в сердцах: «Мне важнее мнение трейдера, чем математика». Тем не менее современная портфельная теория пошла в ход. Я буду повторять, пока не охрипну: судьбу любой социальной теории определяет ее заразность, а не ее обоснованность.

Лишь позже я понял, что финансисты-гауссоведы оккупировали бизнес-школы, а значит, программы МБА, и в одних Соединенных Штатах выпускают в год почти сто тысяч студентов, чьи мозги промыты ложной портфельной теорией. Эпидемию не могут сдержать никакие эмпирические наблюдения. Всем казалось, что лучше уж вооружить студентов теорией, основанной на гауссиане, чем вообще не вооружать никакой теорией. Это выглядело более «научно», чем преподнесение того, что Роберт Кокс Мертон (сын социолога Роберта Кинга Мертона, которого мы обсуждали выше) называл «анекдотами». Мертон писал, что до портфельной теории финансы были «собранием анекдотов, практических правил и способов манипулировать с отчетностью». Портфельная теория позволила «естественно перейти от этого умозрительного крошева к точной экономической теории». Чтобы осознать степень интеллектуальной серьезности, скрывающуюся за всем этим, и чтобы сравнить неоклассическую экономическую теорию с более честной наукой, приведем высказывание жившего в XIX веке отца современной медицины Клода Бернара: «Первым делом — факты, а потом уж — научные дерзания». Надо отправить экономистов в медицинский колледж.

Таким образом, гауссиана [84] проникла в нашу деловую и научную культуру, и такие термины, как сигма, дисперсия, стандартное отклонение, корреляция, R-квадрат и именной коэффициент Шарпа, наводнили язык. Когда читаешь проспект какого-нибудь взаимного фонда или описание рисков хедж-фонда, есть шанс, что тебе предоставят, среди прочей информации, некоторую количественную сводку, претендующую на измерение «риска». Она будет основана на одном из приведенных выше модных словечек. Сегодня, например, инвестиционная политика пенсионных фондов и выбор фондов осуществляются «консультантами», опирающимися на портфельную теорию. Если вдруг возникнет проблема, то они всегда могут заявить, что полагались на общепринятый научный метод.

Дальнейшие ужасы

В 1997 году все стало еще хуже. Шведская академия вручила еще пару «нормально распределенных» Нобелевских премий. Их удостоились Майрон Шоулз и Роберт Кокс Мертон, которые усовершенствовали старую математическую формулу и сделали ее совместимой с великими гауссовыми теориями общего финансового равновесия, а значит, приемлемой для экономического истеблишмента. Теперь формула стала «пригодной к употреблению». У нее был ряд давно забытых «прародителей», среди которых математик и игрок Эд Торп, автор бестселлера «Обыграй сдающего» о премудростях игры в очко, но все почему-то верят, что Шоулз и Мертон ее изобрели, хотя на самом деле они ее просто подправили. Эта формула кормила меня и поила. Трейдеры, люди опыта, столько ночей проводят без сна, размышляя о своих рисках, что знают все ее тончайшие нюансы лучше любого профессора, хотя едва ли могут научно оформить свои мысли; так что я чувствую себя делегатом, выступающим от их имени. Шоулз и Мертон поставили формулу в зависимость от гауссианы, но ее «прародители» не ограничивали ее подобным образом [85] .

Годы после обвала превратились для меня в сплошную интеллектуальную забаву. Посещая конференции по финансам и математике неопределенности, я ни разу не встречал докладчика, с Нобелем или без, который понимал бы, о чем он говорит, когда речь заходила о вероятности, и я доставал их своими вопросами. Они проводили «глубокий математический анализ», но, стоило мне поинтересоваться, откуда они взяли свои вероятности, из их объяснений делалось ясно, что налицо явная игровая ошибка. Это было странное соединение технической подкованности с полным отсутствием понимания. Настоящий ученый идиотизм! Ни разу не получил я разумного ответа или ответа без перехода на личности. Поскольку я ставил под сомнение всю их деятельность, я, понятное дело, навлекал на себя всевозможные оскорбления: «одержимый», «торгаш», «философ», «эссеист», «обеспеченный бездельник», «зацикленный», «делец» (в науке это бранное слово), «профессор» (это бранное слово в бизнесе). Быть обруганным не так уж плохо; к гневным отповедям быстро привыкаешь и сосредоточиваешься на том, что не говорится. Биржевые трейдеры привыкли не обращать внимания на вспышки ярости. В зале биржи всегда найдется кто-то, кто, сильно расстроившись из-за крупной потери, вдруг накинется на тебя с бранью и не умолкнет, пока не наорется до хрипоты, а потом забудет об этом и через час пригласит к себе на Рождество. В результате становишься невосприимчивым к грубостям, особенно если научишься видеть в брызжущем слюной индивиде шумного примата, который плохо отвечает за свои действия. Просто сохраняй спокойствие, улыбайся, оценивай говорящего, а не его речи, и победишь в споре. Нападки на самого интеллектуала, а не на его идею, крайне лестны. Они показывают, что у нападающего нет никаких аргументов.

Психолог Филип Тетлок (из главы 10), послушав один из моих докладов, сказал, что был потрясен царившей в аудитории атмосферой острого когнитивного диссонанса, то есть дискомфорта, возникающего из-за столкновения в сознании двух противоречивых мнений. Но этот когнитивный дискомфорт, связанный с отрицанием самых основ того, чему их учили, методов, которые они применяют и обречены применять, люди могут снимать очень по-разному. Симптоматично, что почти все мои оппоненты атаковали искаженную версию моих рассуждений («все случайно и непредсказуемо» вместо «все в значительной степени случайно») или уходили от темы, показывая мне, как гауссиана работает в некоторых областях физики. Некоторым пришлось даже изменить мою биографию. Однажды на заседании в Лугано Майрон Шоулз в бешенстве принялся громить мои превратно истолкованные идеи. Я видел, как он удручен. Однажды в Париже у видного представителя математической элиты, потратившего часть своей жизни на какое-то мелкое частное свойство гауссианы, «отказали предохранители» — я как раз в ту минуту демонстрировал эмпирические свидетельства влияния Черных лебедей на рынки. Он покраснел от злости, запыхтел и принялся оскорблять меня, обвинив в неуважении к высокому собранию, в котором я находился, и в отсутствии pudeur (скромности); он кричал: «Я член Академии наук!» — чтобы придать больший вес обидным словам. (На следующий день французский перевод моей книги смели с полок.) Но больше всего я люблю историю о том, как Стив Росс, экономист с репутацией интеллектуала, которому Шоулз и Мертон в подметки не годятся, и выдающийся полемист, опровергал мои идеи, указывая на мелкие ошибки или неточности в моем докладе, вроде этих: «Маркович был не первым, кто…», чем подтвердил, что ему нечего сказать о главном. Экономисты часто ссылаются на странное утверждение Мильтона Фридмана: «Чтобы быть приемлемой, модель не обязательно должна исходить из реальных посылок», дающее им право создавать абсолютно дефектные математические образы реальности. Проблема именно в том, что все эти «гауссианизации» не отталкиваются от реальности и не дают результатов, на которые можно было бы положиться. Они нереалистичны и не имеют прогностической силы. Отметим также погрешность восприятия, с которой я часто сталкиваюсь: редкое событие, которое по законам вероятности происходит, скажем, раз в двадцать лет, путают с периодическим. Люди думают, что они в безопасности, если нечто аналогичное случилось всего десять лет назад.

Мне не очень-то удавалось донести до моих слушателей и читателей мысль о разности между Среднестаном и Крайнестаном: представляемые мне возражения в основном сводились к тому, что гауссиана принесла обществу много пользы — посмотрите на кредитные бюро и т.д.

Категорически неприемлемым для меня был только такой комментарий: «Вы правы; спасибо, что напоминаете нам о слабости этих методов; но нельзя же выплескивать с водой ребенка» — примите, мол, наше нисходящее гауссово распределение, признавая вместе с тем возможность больших отклонений. Как не понимать, что эти два подхода несовместимы! Это все равно что быть сразу и живым и мертвым. Ни один из пользователей портфельной теории за двадцать лет моих с ними дебатов не объяснил, как можно принять гауссову структуру вместе с большими отклонениями. Ни один.

Подтверждение

По ходу дела я встретил столько случаев ошибки подтверждения, что Карл Поппер подскочил бы от злости. Эксперты выискивали периоды, не содержавшие скачков или экстремальных событий, и предъявляли мне «доказательство» того, что гауссианой можно пользоваться. Это были примеры сродни моему из главы 5, где я привел «доказательства» того, что О.Дж. Симпсон — не убийца. Все профессиональные статистики путали отсутствие доказательства с доказательством отсутствия. Более того, они даже не подозревали о существовании элементарной асимметрии: достаточно одного-единственного наблюдения, чтобы отбросить гауссиану, но миллионы наблюдений не докажут полностью законность ее применения. Почему? Потому что кривая нормального распределения не допускает больших отклонений, а альтернативные ей инструменты Крайнестана вполне допускают длинные отрезки покоя.

Я не думал, что работа Мандельброта что-то значит за пределами эстетики и геометрии. В отличие от него я не подвергался остракизму: меня одобряли практики и те, кто принимает решения, хотя и не их исследовательские отделы.

Поддержка пришла с неожиданной стороны.

Это был просто Черный лебедь

Роберт Мертон-младший и Майрон Шоулз были сооснователями большой финансово-инвестиционной компании «Лонг-Терм Кэпитал Менеджмент» [86] («ЛТКМ»), о которой я упоминал в главе 4. Все сотрудники имели первоклассные резюме и высочайшие академические степени. Их держали за гениев. Вдохновляясь портфельной теорией с ее хитроумными «алгоритмами», они лихо просчитывали риски и умудрились довести игровую ошибку до чудовищных размеров.

Затем, летом 1998 года, одно за другим последовали несколько значительных событий, спровоцированных русским финансовым кризисом, что не предусматривалось их моделью. Это был Черный лебедь. Компания «Лонг-Терм Кэпитал Менеджмент» лопнула и потащила за собой всю финансовую систему. Поскольку модель, по которой работала «ЛТКМ», исключала возможность больших отклонений, там играли ва-банк. Идеи Мертона и Шоулза, вместе со всей современной портфельной теорией, потерпели крах. Потери оказались настолько впечатляющими, что этот интеллектуальный фарс просто должен был обратить на себя внимание. Я и многие мои друзья полагали, что портфельные теоретики разделят судьбу табачных компаний: они потеряли чужие сбережения и скоро ответят за последствия своих гауссовых подходов.

Ничего подобного.

Портфельная теория осталась в программах бизнес-школ. И формула опциона продолжает носить имя Блэка-Шоулза-Мертона, вместо того чтобы воссоединиться со своими истинными «отцами» — Луи Башелье, Эдом Торпом и другими.

Учитесь «доказывать»

Мертон-младший — представитель экономической школы неоклассиков, которая, как мы видели в случае с «ЛТКМ», нагляднее всего иллюстрирует опасности платонического знания [87] . Глядя на его методологию, я вижу следующую картину. Он начинает с чисто абстрактных посылок, абсолютно нереальных, — таких как гауссовы вероятности и иже с ними. Затем он выводит из них «теоремы» и «доказательства». Математика стройна и элегантна. Теоремы согласуются с другими теоремами современной портфельной теории, которые в свою очередь согласуются еще и с другими теоремами, образующими в совокупности величественную теорию того, как люди потребляют, сберегают, справляются с неопределенностью, тратят и строят планы на будущее. Он исходит из того, что нам известен приблизительный ход событий. Ужасное слово равновесие встречается повсюду. Но все здание подобно абсолютно замкнутой игре с жесткими правилами, вроде «Монополии».

К ученому, применяющему такую методологию, подходит определение, данное Джоном Локком безумцу, — «это тот, кто правильно развивает ошибочные постулаты».

Настоящая, элегантная математика обладает таким свойством: она верна абсолютно, а не на 99 процентов. Это свойство привлекает механистичные умы, которые не хотят разбираться с неоднозначностями. К сожалению, нужно где-то смухлевать, чтобы мир улегся в прокрустово ложе совершенной математики, и надо к чему-то подладить свои постулаты. Но, как показывает цитата из Харди, профессиональные «чистые» математики, по крайней мере, абсолютно честны.

Значит, неразбериха начинается тогда, когда некто вроде Мертона пытается отстаивать стерильную правильность своих математических выкладок, вместо того чтобы задуматься об их соответствии реальности.

Вот где можно поучиться у силовиков. Им плевать на «совершенные» игровые силлогизмы; они хотят отталкиваться от реального, «ощутимого». В конце концов, цена их ошибок — жизни.

Я упоминал в главе 11, что первыми, кто начал играть в «формальное мышление», фабрикуя липовые посылки с целью породить «точные» теории, были Пол Сэмюэлсон, наставник Мертона, и, в Соединенном Королевстве, Джон Хикс. Эти двое загробили идеи Джона Мэйнарда Кейнса своей попыткой их формализовать (Кейнс интересовался неопределенностью и сетовал, что жесткие модели сужают кругозор). Поборниками формального мышления были также Кеннет Эрроу и Жерар Дебрё. Все четверо — нобелиаты. Все они находились под чарами ее величества математики — такое состояние Дьедонне называл «музицированием разума», а я называю «безумием Локка». Всех их можно смело обвинить в создании воображаемого мира, в котором их математика — неограниченная властительница. Проницательный ученый Мартин Шубик, считавший, что крайняя степень абстрактности этих моделей (на несколько уровней выше необходимого) делает их совершенно непригодными, подвергся остракизму, как обычно бывает с инакомыслящими [88] .

Если вы усомнитесь, как я, в ценности достижений таких людей, как Мертон-младший, они потребуют «стройного доказательства». То есть они задают правила игры, и вы должны играть по ним. Как выходец из деловой среды, где главная ценность — это умение применять путаную, но эмпирически приемлемую математику, я не признаю претензий на ученость. Выморочной науке, ищущей определенности, я предпочитаю процветающее и изощренное ремесло, которое сродни трюкачеству. А может, эти модельеры-неоклассики заняты чем-то похуже? Может, они заняты тем, что епископ Юэ назвал производством определенностей?

Давайте разберемся.

Скептический эмпиризм защищает противоположный метод. Мне важнее посылки, чем теории. Я хочу минимально зависеть от теорий, прочно стоять на собственных ногах и жить, по возможности, без сюрпризов. Я хочу быть более или менее прав, а не точно неправ. Изящество теории часто указывает на ее платоничность и слабость — оно искушает тебя, заставляя искать изящество ради изящества. Теория — как лекарство (или правительство): часто бесполезна, иногда необходима, всегда своекорыстна и иногда смертельна. Поэтому ее надо использовать осторожно, умеренно и под тщательным наблюдением взрослых.

Различие в таблице, приведенной выше, между моим образцовым современным эмпириком-скептиком и тем, что представляют собой «щенки Сэмюэлсона», можно перемести и на другие дисциплины.

Я изложил свои идеи в области финансов, потому что там я отточил их. Рассмотрим теперь категорию людей, от которых принято ожидать большей раздумчивости, — философов.

Глава 18. Неопределенность «липы»

Философы где не надо. — Неопределенность видов (прежде всего) на обед. — Что мне безразлично. — Образование и интеллект.

В этой главе, последней в третьей части, мы сфокусируемся на важнейшей разновидности игровой ошибки: на том, как люди, чья профессия — напоминать нам о неопределенности, обманывают нас, уводя к мнимой определенности через черный ход.

Снова об игровой ошибке

Я объяснил игровую ошибку с помощью истории про казино и сделал упор на том, что стерилизованная случайность игр непохожа на случайность в реальной жизни. Взглянем снова на рисунок 7 в главе 15. Результаты бросков монетки усредняются так быстро, что я могу с уверенностью сказать: у казино уйдет не слишком много времени на то, чтобы обставить меня, скажем, в рулетку, так как колебания уравновесятся, а мастерство — нет (здесь первенство за казино). Чем дольше период (или чем мельче ставки), тем меньше в этих игорных механизмах остается случайности.

Игровая ошибка берет свое начало в следующих вероятностных системах: в случайном блуждании, в метании костей, в подбрасывании монетки, в броуновском движении (соответствующем движению частиц пыльцы в воде) и тому подобном. Эти системы порождают такую случайность, которую и случайностью-то не назовешь, скорее уж протослучайностью. По существу, все теории, построенные на игровой ошибке, игнорируют огромный пласт неопределенности. Хуже того, их поборники об этом не догадываются.

Один из ярчайших примеров этой сосредоточенности на малой, в ущерб большой, неопределенности — банальный принцип неопределенности.

Найди «липу»

Принцип неопределенности гласит, что в квантовой механике невозможно измерить (с произвольной точностью) некоторые пары величин — такие как координата и импульс частиц. Вы упретесь в нижний предел точности измерений: пока одно уточняется, другое меняется, и так до бесконечности. Таким образом, существует несжимаемая неопределенность, которая, в теории, будет бросать вызов науке, вовеки таковой оставаясь. Эта крохотная неопределенность была открыта Вернером Гейзенбергом в 1927 году. По-моему, представлять принцип неопределенности в какой-то связи с неопределенностью просто смешно. Почему? Во-первых, это гауссова неопределенность. В среднем она исчезает — напомню, что вес одного человека не в состоянии значительно изменить общий вес тысячи человек. Мы можем всегда пребывать в сомнении относительно будущих положений мелких частиц, но эти неопределенности очень малы и многочисленны, и они усредняются — черт побери, они усредняются! Они подчиняются закону больших чисел, который мы обсуждали в главе 15. А большинство типов случайности не усредняется! Если есть на нашей планете что-то более определенное, то это — поведение совокупности субатомных частиц! Почему? Потому что, как я сказал ранее, когда перед вами объект, представляющий собой совокупность частиц, колебания этих частиц уравновешиваются.

Но политические, общественные и погодные явления лишены этого удобного свойства, и мы не в состоянии их с точностью предсказать, так что когда вы слышите «эксперта», низводящего проблемы неопределенности на уровень субатомных частиц, вероятнее всего, этот эксперт — «липовый». Можно сказать, что это лучший способ распознать «липу».

Люди часто говорят: «Конечно, наши знания не безграничны» — и тут же приводят принцип неопределенности в оправдание того, что «невозможно все смоделировать», — я слышал это на конференциях от таких видных экономистов, как Майрон Шоулз. Но вот я сижу в Нью-Йорке в августе 2006 года, снедаемый желанием попасть в свое родное селение Амиун в Ливане. Аэропорт Бейрута закрыт из-за конфликта между Израилем и шиитской вооруженной группировкой «Хезболла». Нигде не вывешено расписание рейсов, которое уведомило бы меня, когда кончится война и кончится ли она вообще. Я не могу узнать, выстоит ли наш семейный дом, сохранится ли Амиун на карте, — вспомним, что наш дом уже был однажды разрушен. Я не могу узнать, переродится ли эта война во что-то еще более жестокое. Глядя на войну, которая затрагивает всех моих родственников, друзей и мою собственность, я сталкиваюсь с истинными границами знания. Может кто-нибудь объяснить, почему я должен беспокоиться о субатомных частицах, которые все равно сходятся к гауссиане? Человеку не дано предугадать, долго ли будут тешить его только что купленные обновки, сколько продлится его брак, что ждет его на новой работе, но именно на субатомные частицы ссылается он, как на доказательство «предела, положенного нашим прогнозам». Стоящий у всех на виду мамонт оказывается забытым ради материй, которых не рассмотреть даже в микроскоп.

Могут ли философы быть опасны для общества?

Я пойду дальше: те, кто беспокоится о пенсах, а не о долларах, могут быть опасны для общества. Они хотят как лучше, но (как ясно из моих рассуждений о Бастиа из главы 8) от них очень много вреда. Они мешают исследованию неопределенности, сосредоточиваясь на мелочах. Наши ресурсы (как познавательные, так и научные) ограниченны, может быть, слишком ограниченны. Те, кто отвлекает нас, увеличивают риск появления Черных лебедей.

Такое измельчание понятия неопределенности, как симптом неспособности видеть Черных лебедей, стоит обсудить отдельно.

Поскольку все финансисты и экономисты по уши погрязли в гауссиане, я стал искать финансовых экономистов с философским уклоном, чтобы понять, позволяет ли их критическое мышление справиться с этой проблемой. Нескольких я действительно нашел. Один из них получил докторскую степень по философии, затем, через четыре года, по финансам; у него имелись статьи по обоим предметам и куча учебных пособий по финансам. Но этот тип меня удручил: создавалось впечатление, будто он разложил свои мысли о неопределенности по разным ящичкам, то есть что у него две разных специальности — философия и финансовые расчеты. Проблема индукции, Среднестан, эпистемическая непроницаемость или опасные допущения гауссианы не казались ему достойными внимания. Его многочисленные учебники вдалбливали гауссовы методы в головы студентов, как будто их автор забыл, что он философ. Зато он своевременно вспоминал об этом, когда сочинял философские «этюды» на якобы научные темы.

Та же «ареал-специфичность» заставляет людей подниматься в фитнес-центр на эскалаторе, но случай с философом во сто крат опаснее, ибо наш ограниченный запас критического мышления расходуется тут вхолостую. Философы любят расточать свою философскую премудрость на предметы, которые другие философы называют философией (по принципу «как ты, так и я»), и оставляют мозги у дверей, переходя к чему-то иному.