Георгий Малинецкий, Алексей Потапов

Наверное, у тех, кто прочитал не один десяток толстых книг «с формулами», прослушал сотни лекций и докладов на разных конференциях, рано или поздно возникает несколько вопросов. Почему, несмотря на всю сложность мира, в чем-то удается разобраться? Почему подчас довольно простые эксперименты могут давать ответы на глубокие фундаментальные вопросы? Почему в причудливом переплетении десятков разных процессов удается отыскать новый эффект? О путях развития науки, поисках совершенно новых способов решения задач, перед ней встающих, о синтезе наук на новом уровне — размышления авторов. И адресованы они не только ученым — вот, что самое интересное.

ИГРЫ СЛОЖНОСТИ

Способны ли вы вообразить шесть чисел, связанных с каждой точкой пространства? Это слишком трудно. А можете ли вы вообразить хотя бы одно число, связанное с каждой точкой пространства? Я лично не могу!
Р. Фейнман

Действительно, почему, несмотря на все принципиальные и методические трудности, ученые продвигаются вперед? Можно удовлетвориться ответом, предлагавшимся Галилео Галилеем. Классик полагал, что книга Природы написана языком математики. Исаак Ньютон связывал успехи в познании Вселенной с глубиной и величием божественного замысла. Позже вопросы познаваемости и границ нашего знания адресовали философам. Большинство из них тогда, как и сейчас, с легкостью решали все проблемы, мучившие незадачливых естественников. XX век внес в эту картину существенные коррективы. Оказалось, что на нынешнем уровне развития науки можно создавать междисциплинарные подходы. Они позволяют мыслить многое как единое, оставаясь на твердой почве конкретных задач, методов, уравнений. Первым таким подходом стала кибернетика, созданная трудами Норберта Винера, его коллег и последователей.

Вихри, возникающие при обтекании цилиндра набегающим потоком жидкости (или, как их называют, дорожка Кармана). Красивые структуры, простая и очаровательная упорядоченность

Первой междисциплинарной наукой стала в XX веке кибернетика, созданная трудами Норберта Винера, его коллег и последователей.

В семидесятые годы закладывались основы нового междисциплинарного подхода — синергетики, теории самоорганизации, теории диссипативных структур. Слово «самоорганизация» здесь является ключевым. Возникновение этого научного направления связывают с именами бельгийского ученого Ильи Пригожина и немецкого теоретика Германа Хакена. Пожалуй, главным достижением этого научного подхода стало понимание того, почему многие сложные системы могут вести себя просто.

В семидесятые годы появился новый междисциплинарный подход — синергетика, теория самоорганизации. Здесь слово «самоорганизация» — ключевое.

Именно эта простота и позволяет в чем-то разобраться, дает возможность строить простые модели сложных явлений.

Спросим себя, что такое «сложность»? Наивный ответ, который нас сейчас вполне устроит, состоит в следующем. Чтобы описать какой-нибудь объект (то есть полностью определить его состояние), математику, скажем, нужно задать N чисел. Чем больше N, тем сложнее объект. Величину N математики красиво называют размерностью фазового пространства.

В нашем веке в естествознании, в математическом моделировании большую популярность завоевали объекты, в которых величина N бесконечна. Таковы, например, уравнения электродинамики — чтобы описать электромагнитное поле в данный момент, нужно задать шесть чисел в каждой точке пространства. (Именно к ним относятся слова Р. Фейнмана, вынесенные в эпиграф.) В простейших задачах квантовой механики — два числа, в гидродинамике — пять.

Почему же, имея дело с такими объектами, можно строить модели каких-то явлений и тем более их использовать? Разгадку подсказывает рисунок 1. На нем показаны вихри, возникающие при обтекании цилиндра набегающим потоком жидкости (или, как их называют, дорожка Кармана). Видно, что мы имеем дело с красивыми структурами, простой и очаровательной упорядоченностью. Числа, характеризующие среду в каждой точке пространства, оказываются согласованы, а не произвольны. Поэтому такие структуры иногда называют «когерентными», а числа N, характеризующие их, могут быть небольшими — 3, 10, 100, а вовсе не бесконечными.

Результаты моделирования некоторой химической раекции. Впрочем, структуры, возникающие в полупроводниках, в развивающейся ткани, плотность популяции для некоторых хищников и их жертв выглядит примерно так же

Однако самоорганизацию, процесс возникновения структур удобнее проследить на примере компьютерного расчета, представленного на рисунке 2. Здесь показаны результаты моделирования некоторой химической реакции. Впрочем, структуры, возникающие в некоторых полупроводниках, в развивающейся ткани, плотность популяций для некоторых хищников и их жертв выглядят примерно так же. На то она и междисциплинарность. Показаны распределения концентраций в различные моменты времени. Начальные данные имеют очень сложный вид, для их описания нужно очень много чисел (труднее всего описывать «мусор»). Но затем, как по мановению волшебной палочки, картина упрощается и возникают замечательные структуры. Распределения становятся похожи на синусоиды, а их-то описывать совсем легко. Роль волшебной палочки в образовании структур играют диссипативные процессы — вязкость, теплопроводность, диффузия (от английского to dissipate — рассеивать). Чтобы подчеркнуть этот факт, И. Пригожий назвал структуры, возникающие при самоорганизации, диссипативными.

Не удивительно, что представители самых разных научных конфессий активно, энергично и успешно находили диссипативные структуры в своих областях. Казалось бы, все дальнейшее просто. Поскольку из-за самоорганизации, величин, необходимых для описания объекта, остается немного, можно строить модели, разбираться в разных процессах и прогнозировать их ход: задать начальные данные и, решив уравнения, например, с помощью компьютера, посмотреть, что будет дальше. Или, на языке математиков, построить фазовую траекторию. При этом могут получиться, например, такие кривые, как показано на рисунке 4. Обратим внимание на то, что через каждую точку фазового пространства проходит только одна траектория. Это ньютоновское выражение принципа причинности — будущее однозначно определяется прошлым. Казалось бы, имея такую модель, можно предсказывать состояние системы сколь угодно далеко вперед — надо только вычислить траекторию. Лаплас и полагал, говоря нынешним языком, что мощная вычислительная техника в принципе позволит заглянуть, как угодно далеко. Чем мощнее техника, тем дальше можно заглянуть.

Однако тут на сцену выступил его величество Детерминированный Хаос, который и спутал карты ученых. Это явление настолько просто, красиво и парадоксально, что остается лишь удивляться, почему оно не было открыто полвека, а то и век тому назад. Попытки понять его и научиться с ним обращаться, привели к рождению второй парадигмы, которую обычно называют нелинейной динамикой. Английский эквивалент этого названия — monlinear science — нелинейная наука, звучит несколько странно, как бы подразумевая, что какие-то науки остались «линейными».

Его величество Детерминированный Хаос — явление настолько простое, красивое и парадоксальное, что остается лишь удивляться, что оно не было открыто полвека, а то и век тому назад.

Геометрически эволюция объекта соответствует пути, траектории в фазовом пространстве, о котором уже шла речь. Например, траектория может иметь вид «клубка», изображенного на рисунке 3. Здесь пространство всего лишь трехмерно (N = 3). Этот причудливый клубок появляется со временем в модели, связанной с описанием конвективных ячеек, показанных на рисунке 1. Американский метеоролог Эдвард Лоренц, построивший такую модель, хотел разобраться, почему так трудно получить двух- и трехнедельный прогноз погоды. Позже выяснилось, что «клубок» имеет отношение к динамике лазеров, перемешиванию коктейлей и системам охлаждения атомных станций.

«Клубок» и другие объекты такого сорта, который математики называют красивым словом «странные аттракторы» (от английского to attract — притягивать), убедили, что дело может обстоять иначе. Начальное состояние мы определяем с ошибкой, пусть даже очень маленькой. Понятно, что если со временем ошибка между тем, что мы предполагали, и тем, что есть на самом деле, быстро увеличивается, то и предсказания делать трудно. Наш мир устроен таким образом, что во множестве самых разных систем ситуация именно такова. Так дело обстоит с погодой и изменениями климата, с солнечной активностью и многими операциями на бирже, с некоторыми биохимическими реакциями и электрической активностью мозга. Оказалось, что подобные системы обладают внутренней неустойчивостью, которая, однако, не разрушает их, а приводит к сложному поведению с ограниченной предсказуемостью. Существует горизонт прогноза. И трудности здесь не технические, которые можно обойти, прикупив более мощный компьютер, а принципиальные.

Существует горизонт прогноза. Это такое же серьезное препятствие в исполнении наших желаний, как существование максимальной скорости передачи сигналов или невозможность создания вечного двигателя.

Геометрическая эволюция объекта соответствует его траектории в фазовом пространстве. Например, траектория может иметь вид “клубка”. Такой клубок имеет отношение к динамике лазеров, прогнозу погоды и перемешиванию коктейлей

Это такое же серьезное препятствие в исполнении наших желании, как существование максимальной скорости передачи сигналов или невозможность создания вечного двигателя, несмотря на все остроумие предлагавшихся конструкций. Впрочем, нелинейная динамика не только объяснила, чего «нельзя», но и показала, что «можно» и как этого добиться. Со страниц научных журналов методы нелинейной динамики перешли в сферу прикладных задач, банковских технологий, медицинской диагностики, криптографии, стратегического планирования. Возникли процветающие компании компьютерных прогнозов, международные журналы «Хаос», «Нелинейность», «Хаос, солитоны и фракталы» и десятки других.

И все же, все же, все же…

Алхимия финансов и первые джокеры

Сложные системы приводят к неожиданным последствиям
Из законов Мерфи

Компьютер очень сильно расширил возможности исследователей, но и у этой области есть свои границы и подводные камни. Попытка брать «числом» (быстродействием, объемом памяти), а не «умением» (новыми постановками задач, алгоритмами) тут не проходит.

Да и нелинейной науке приходится нелегко. В популярном сборнике «Физики шутят» была такая житейская мудрость: «Если в задаче меньше трех переменных, это не задача; если больше восьми — она неразрешима». Примерно так же можно сказать о современной нелинейной динамике: «Если N меньше четырех, то все можно понять, если меньше десяти, то все можно посчитать, а дальше начинается область магии».

Итак, за сложностью можно часто увидеть простоту, написать простую модель и найти траекторию. Даже хаос имеет свой порядок внутри себя и этот порядок зачастую не слишком сложен. Однако на пути моделирования сложных объектов подстерегают и другие трудности. Одна из них связана с тем, что в сложных системах существует большой «резерв сложности» в поведении, и они этим резервом иногда пользуются. В результате может оказаться, что наша простая модель больше не работает.

В точных науках не принято говорить о таких ситуациях. Усложнение чаще всего описывают в рамках теории бифуркаций как постепенное увеличение величины N, происходящее при очень плавном изменении каких-нибудь параметров. В социальных же науках, куда математика и моделирование проникли слабо, подобные ситуации не редкость. Один из хороших примеров подробно описан Дж. Соросом в его книге «Алхимия финансов».

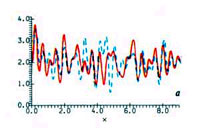
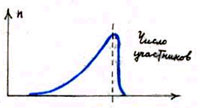
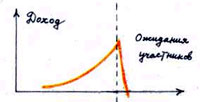
Сорос обнаружил интересную закономерность в изменении прибыльности многих успешных финансовых проектов. Если проект достаточному количеству людей кажется прибыльным, они вкладывают в него деньги. После того как деньги вложены, проект и в самом деле становится прибыльным. Ожидания подтверждаются, и это порождает новые вложения. Вложения снова могут увеличить прибыльность. Так возникает лавина, бум ожиданий. Включается положительная обратная связь. Динамика прибыльности, цены акций и тому подобное становятся предсказуемыми и могут быть довольно просто описаны (как, например, у Сороса). Такую картину иллюстрирует рисунок 5, на котором показаны число инвесторов, их ожидания и реальная доходность предприятия.

Однако в конце концов ресурсы развития оказываются отчасти исчерпаны и предприятие больше не дает той доходности, на которую все рассчитывали. После этого включается обратный механизм: инвесторы начинают забирать деньги, это снижает прибыльность и порождает очень быстро усиливающийся дальнейший отток средств. Предсказуемость дальнейшей судьбы предприятия резко ухудшается, потому что она начинает зависеть от множества факторов, которые ранее были несущественны…

Сороса эта ситуация заинтересовала с точки зрения коренных отличий гуманитарных наук от естественных: в экономике, а особенно на финансовых рынках будущее в значительной степени творится ожиданиями участников игры. Поэтому для достижения нужных результатов иногда необходимо изменить эти ожидания в свою пользу, а затем, если расчет был верный, в течение некоторого времени будет идти самоподдерживающийся процесс. Мы не будем пересказывать первоисточник. Отметим только, что Сорос основную проблему видит в необходимости учета ожиданий в адекватных математических моделях (в отличие от классических экономических теорий). Его волнует проблема рефлексии. Нам же этот пример интересен с другой точки зрения, как простой и в то же время типичный пример ситуации, когда плавное течение ситуации вдруг сменяется резким провалом, как будто спокойно плывущий корабль вдруг натыкается на рифы.

Итак, в отличие от типичных ситуаций естественных наук, у нас появилась переменная, которая может меняться скачками. В этот момент поведение объекта может резко усложниться (как будто бы N резко возросло), а горизонт прогноза — сократиться. В примере Сороса происходит смена одних ожиданий, общих для всех, другими, разными для всех участников рынка. Таковы же и времена смут. По мнению В. О. Ключевского, в смутное время жизнь общества до чрезвычайности усложнялась, классы выступали со своими требованиями и претензиями и прихоти «польских шаек» или «тушинского вора» могли существенно отразиться на судьбах России. То есть уравнения, правила, нормы морали и поведения, пригодные для спокойного этапа, вдруг становятся непригодными, перестают давать верный прогноз, соблюдение старых норм не ведет к успеху.

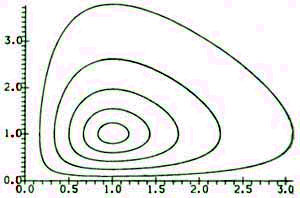
Здесь через каждую точку фазового пространства проходит одна кривая. Казалось бы, имея такую модель, можно предсказывать состояние системы далеко вперед. Однако это далеко не так, и даже мощная техника здесь не поможет

Для описания таких ситуаций пришлось ввести новый класс моделей — динамические системы с джокерами. Напомним, что в большинстве карточных игр джокер (от английского joker — шутник) может быть назначен любой картой, по желанию того, кому он достался. Это резко повышает неопределенность ситуации и усложняет игру. Пусть мы с вами играем в покер, джокеров в колоде нет, и вы делаете вид, что у вас на руках четыре короля — каре. Если при этом у нас есть король, то сразу ясно, что вы блефуете. Но если в колоде есть джокер, то все не так очевидно. Надо прикинуть, каков ваш опыт игры, темперамент, склонны ли вы сегодня к риску и еще многие другие факторы.

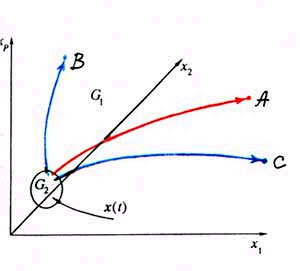
Итак, мы рассмотрим привычное фазовое пространство, в котором есть маленькая область G2, которую называют областью джокера, и все остальное G1. Когда точка, соответствующая положению нашей системы, находится в G1, все происходит как всегда. Будущее однозначно определяется прошлым, траектории гладкие и непрерывные. Но, допустим, траектория подошла к области G2. Тут в дело вступает джокер. Так специалисты по моделированию назвали правило, которое определяет дальнейшее. В соответствии с ним система может совершить скачок, величественная финансовая пирамида рухнула, и маловероятный шанс станет грустной реальностью.

Теперь немного «прикладной джокерологии». Джокеры бывают разные.

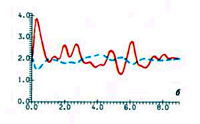
Джокер первого рода скачком перебрасывает нашу систему из области джокера в точку А (красная стрелка на рисунке 6). Такие модели могут описывать ситуацию, в которой мы пилим сук, на котором сидим. Сначала все идет отлично, работа кипит, средства осваиваются, сук становится все тоньше. И потом…, как и следовало ожидать, мы оказываемся на земле.

Джокер второго рода действует хитроумнее. С вероятностью р1, он переводит систему в точку В, с вероятностью р2 — в точку С (синие стрелки на том же рисунке). Простой жизненный пример здесь таков. Представим, что дела в вашем с вами банке идут все хуже и хуже (ученым приходится размышлять и над такими невероятными ситуациями). Пора что-то решать. С вероятностью р1 мы объявляем изумленным вкладчикам о банкротстве нашего процветающего банка, а с вероятностью р2 устраиваем презентацию в «Хилтоне». Реклама, пресса, новые вкладчики.

Джокер третьего рода еще коварнее. Он может перевести наш объект в любую точку пространства, но с разной вероятностью. Читатели, конечно, догадались, что речь идет о рэкете, а «объект» — это семейный бюджет. К вам приходят спортивного вида молодые люди и делают предложение, от которого невозможно отказаться. Друзья и знакомые со спокойной грустью мудрых людей советуют платить. И, естественно, разные суммы придется платить с разной вероятностью

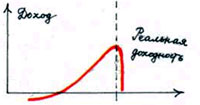Динамика прибыльности, цены акций могут стать предсказуемы с точки зрения моделирования процесса. На рисунке показано число инвесторов, их ожидания и реальная доходность предприятия

Джокеры начали свою жизнь в науке менее года назад, но уже сейчас нашлось много задач, где их применение оказывается полезным или дает интересные результаты. Например, это экспертные системы и системы поддержки принятия решений. Принятие крупных решений относится к одной из важнейших технологий в современном мире, включающих сложные компьютерные системы, различные процедуры, привлечение экспертов в различных областях («академик по котам, академик по китам», как в книге Б. Заходера). Если мы четко знаем область джокера (определение которой требует отдельной работы), то становится ясно, когда одних специалистов надо благодарить за сотрудничество и привлекать других. Когда, например, следует отказаться от услуг терапевтов и срочно звать хирургов.

Джокеры могут не только усложнять ситуацию, но и упрощать ее. Они могут превратить хаос в сложную упорядоченность заданного типа. Многие интересные эффекты, связанные с джокерами, напоминают поведение некоторых химических реакций. Однако для нашего разговора важнее другое. Джокеры и другие системы такого типа — это механизмы упрощения реальности. Это способы отказаться от анализа одних факторов, от одних стратегий, чтобы перейти к другим. И, судя по эволюционным успехам нашего вида, — способы неплохие.

Русла и проекции реальности

Мы не ставим своей задачей построение общей теории, а хотим сосредоточиться лишь на частичном объяснении динамики…
Дж. Сорос. «Алхимия Финансов»

Вероятно, в полной мере проблему помогли осознать суперкомпьютеры. Один специалист определил их как ЭВМ, которые на поколение отстают от задач, которые на них решают. Их использование в задачах прогнозирования показало, насколько сложные задачи приходится решать живым организмам, как совершенны их прогнозирующие системы. Может быть, все дело в суровом экзаменаторе. Природа жестко дисквалифицирует всех, кто плохо решает. Более того, психологи утверждают, что ключевым звеном в обучении является опережающее отражение. Ни у зайца, который убегает от волка, ни у оператора атомной станции нет возможности учиться на собственных ошибках (второй попытки просто не будет). Приходится учиться, осмысливать окружающее, совершенствовать предсказывающую систему и здравый смысл.

Использование суперкомпьютеров в прогнозировании показало, насколько сложные задачи приходится решать живым организмам, как совершенны их — прогнозирующие системы. Может быть, все дело в суровом экзаменаторе. Природа жестко дисквалифицирует те, кто плохо решает.

Системный анализ, теория исследования операций, а теперь и нелинейная динамика — дисциплины, связанные с прогнозом, с компьютерной обработкой огромных массивов информации, показали, насколько важной и тонкой вещью является этот пресловутый здравый смысл. Специалисты по моделированию столкнулись с очень серьезным ограничением — прогноз следует давать не вообще, а в реальном масштабе времени. В тысячах ситуаций, где самые современные алгоритмы и суперкомпьютеры пасуют, интуиция и опыт позволяют найти разумный компромисс. Почему? Потому что мозг обладает поразительной способностью упрощать мир, выбирать ключевые переменные, самые главные процессы и причинно-следственные связи, верную проекцию реальности. Причем в разных ситуациях разную! Развитие вычислительных систем показало, что эта способность гораздо более удивительна, чем загадочная архитектура мозга, позволяющего решать нестандартные задачи, или таинственная память, преподносящая парадоксальные ассоциации

Если мозг выбирает самое главное и существенное из огромного пространства нашей реальности, значит, оно в ней есть.

Однако, если мозг выбирает самое главное и существенное из огромного фазового пространства нашей реальности, значит, оно в ней есть. Но тогда это можно отобразить в математических моделях. (Если Декарт говорил, что он мыслит, следовательно, существует, модельер может сказать, что он понимает, если может построить математическую модель.) Однако классические математические модели не приспособлены к резким изменениям ситуации — все, что может случиться, фактически уже заложено в модель при ее создании (поэтому модели и позволяют делать открытия). Однако создавать слишком сложные модели, которые содержали бы сразу же все, бессмысленно. Как показывает опыт математического моделирования, их невозможно будет проанализировать. Где же выход?

Итак, в нашем фазовом пространстве есть джокеры. От них одни стараются держаться подальше (как в пословице: «Умный найдет выход из любой ситуации, а мудрый в нее просто не попадет»), а другие активно использовать (знаменитое наполеоновское: «Главное ввязаться в драку, а там посмотрим»). В них неопределенность резко возрастает, а возможности предсказывать дальнейшее уменьшаются. Следовательно, должны быть и другие области, в которых многое или хотя бы самое существенное можно предсказать. Возможно, умение их быстро и точно находить и является главным козырем нашей нервной системы.

Такие области мы будем называть руслами. Название ясно из картинки 7. Близкие траектории как бы притягиваются к некоторому пучку, трубке и далее следуют вместе. Значит, зная детально одну траекторию, можно многое сказать и о других. Политологи, консультанты, референты со времен Римской империи знают, что если в провинции Анчурии заговорили о возрождении национального языка и культуры и о славной истории анчурийского народа, то центр ослаб и большие беспорядки не за горами.

Важно отметить, что картина сближающихся траекторий может наблюдаться не для всех переменных, характеризующих систему, а только для нескольких. Отбрасывая остальные как несущественные («стирая случайные черты»), мы получаем проекцию реальности, в которой ситуация становится предсказуемой, хотя, возможно, с ограниченной точностью и в течение ограниченного промежутка времени. Насколько успешной окажется такая проекция — зависит от системы. Это определяется тем, насколько отброшенное способно повлиять на избранные кандидатуры существенных переменных.

По-видимому, большинство успешных научных теорий приводит к успеху, когда проекция реальности, с которой они имеют дело, оказывается связана с каким-либо руслом (или, если хотите, создание такой успешно предсказывающей теории и показывает, что русло существует и найдено). В идеальном случае очень устойчивых причинно-следственных связей можно оставаться в рамках логики, конструкций типа «Если… то» и навсегда забыть о несущественных деталях. Это и будет обычная математическая модель. Тут раздолье для идеализации, для людей, которые умеют доказывать теоремы.

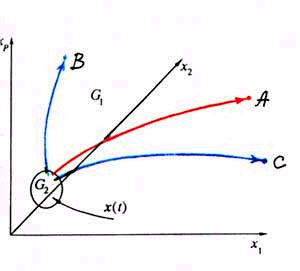
Джокеры бывают разными. Описание их действий вы найдете в тексте статьи

На следующем уровне находится физика. Ей посчастливилось — она в большинстве ситуаций имеет дело с глобальными руслами, когда можно выделить и описывать почти изолированную подсистему (об окружении можно забыть почти всегда), когда существенными оказываются одни и те же переменные и можно всегда пользоваться одними и теми же уравнениями (дополнительность является скорее исключением, а не правилом). Правда, до теорем обычно дело не доходит, да и на бумажке можно посчитать немного, приходится часто обращаться к помощи компьютера.

В экономике, социологии, психологии, истории ситуация сложнее. Успехи выдающихся экономических теорий, различных психологических школ показывают, что русла есть и здесь. Однако, во-первых, они локальны, то есть обладают предсказывающей силой только в какой-то вполне определенной ситуации. А во-вторых, от них нельзя требовать очень точных и очень длительных прогнозов (хотя от создателей можно потребовать эту точность оценить). Поэтому нужно очень точно оговаривать допущения, исходные посылки. На первый план выходит определение истока (когда посылки начинают быть справедливы) и устья русла (когда они больше не выполняются), определение джокеров — если нельзя указать следующее русло.

Почему русла важны? Потому что понимание, на основе которого можно принимать решения, дают только простые модели, а втиснуть в них действительность можно только отбрасывая «лишнее». По-видимому, на подсознательном уровне мозг решает подобные задачи очень быстро, однако сознательный выбор нужных переменных и его обоснование требует времени, иногда очень большого. Ведь умели же люди очень точно кидать камни и пускать стрелы задолго до Галилея и Ньютона. Мозг быстро прикидывает нужные траекторию и усилия, но никто точно не знает, каким образом. Надо только немного потренироваться. Преуспевающие бизнесмены хорошо ориентируются на биржах и рынках, но обычно не создают экономических теорий и, видимо, почти не пользуются ими. То же самое наблюдается в управлении коллективами людей, сложными объектами, в нетрадиционной медицине и тому подобное. Однако такое эмпирическое знание хотя и приводит к успеху, обычно не может быть передано другим людям, не становится достоянием общества. Его можно передавать только небольшой группе близких соратников личным примером, да и то не всегда. Ученые же теории создают, но социальные теории обычно успешнее всего объясняют прошлое. Пока теория создается, ситуация успевает измениться и старая проекция уже может не отражать сути дела. Найденное русло оказалось пройдено, и текущая ситуация соответствует джокеру или пока не найденному руслу в неизвестной проекции.

Что же делать в такой ситуации? Принципиальным становится определение структуры нашего незнания, осмысление ситуаций, где еще могут существовать русла, и также техники, позволяющей переходить от одних русел к другим, от одних теорий к их альтернативам. Может, к примеру, оказаться, что неокейнсианство и монетаризм — это не альтернативное описание одной реальности, а теории, относящиеся к разным руслам. Поэтому может оказаться, что вопросы «Вы за или…», «Кто прав?» лишены смысла. Следует просто осознать, к какой теории ближе реальность, которую предполагают моделировать или тем более менять. Это необходимо, чтобы не пришлось «импровизировать» или, хуже того, «подгонять» существующую реальность под неадекватную теорию.

Вероятно, именно здесь и может быть развита новая парадигма нелинейной динамики и математического моделирования. Зачем вообще она нужна? Дело в том, что класс объектов, для которых удается строить эффективные модели «из первых принципов», на наш взгляд, в настоящее время почти исчерпан. Для решения многих важных и актуальных задач необходимо строить предсказывающую модель исходя из известной предыстории объекта (подобно тому, как мозг обучается довольно точно бросать камень по результатам тренировочных попыток). И здесь мы встречаемся с серьезнейшими ограничениями на сложность модели. Как показывают некоторые результаты нелинейной динамики, число N здесь обычно не может превышать 5-10. Возможно, следует отказаться (хотя бы частично) от построения общих теорий, а «сосредоточиться лишь на частичном объяснении динамики», на создании «частных теорий», для построения которых было бы достаточно сравнительно небольшого объема информации.

Такого, который может быть собран, переработан и осмыслен за разумный промежуток времени. И для этого концепция русел и джокеров представляется многообещающей. (Здесь уместно будет заметить, что авторы не претендуют на то, что они изобрели нечто принципиально новое. Скорее всего, элементы такого взгляда на научное познание можно найти еще у древних авторов. Мы только хотим подчеркнуть, что предлагаемая концепция позволяет предложить разумное решение ряда серьезных проблем. Именно такой смысл мы вкладываем в слова «третья парадигма».)

Определение русел и джокеров в социальных науках, экологии, теории риска представляется захватывающей задачей. Организация общества, устойчивость и безопасность развития, благополучный внутренний мир выходят на первый план, оттесняя на второй гонку технологий, императивы общества потребления.

Более того, здесь нужен иной уровень междисциплинарного сотрудничества. К сожалению, авторам не раз доводилось сотрудничать на других уровнях. Одни гуманитарии хотели научиться писать украшенные формулами статьи. Другие хотели сначала обсудить методологические проблемы и проверить, можно ли пускать математиков в святая святых. Впрочем, и некоторые наши коллеги-естественники были склонны объяснять, что «многое» в истории, начиная с датировки и кончая никудышной статистикой, следует выбросить на свалку.

Здесь придется учиться слушать и понимать друг друга, искать русла, параметры порядка, проекции реальности.

А что дальше?

Сложные проблемы всегда имеют простые, легкие для понимания неправильные решения.
Из законов Мерфи

Прекрасно только то, что нетрудно понять.
А. Франс

Можно предположить, что эра сверхспециализации, рождения наук на стыке разных дисциплин, уходит в прошлое. Ей на смену идет эра синтеза. Если в XX веке доскональное углубленное изучение одного русла и некоторой любимой проекции считалось почетным и благородным занятием, то в XXI веке у профессионалов будут спрашивать, как перейти от одного русла к другому и где на этом пути могут встретиться коварные джокеры. Методы анализа одних проекций могут оказаться полезными для других. С точки зрения русел, интересно взглянуть и на некоторые проблемы человеческого познания. Например, философия с этой точки зрения видится как попытка найти универсальную проекцию (систему понятий и терминов), в которой единообразно описывался бы весь мир — то есть самое глобальное русло. Искусство идет в противоположном направлении. Его больше интересует неповторимое, то, что в единую проекцию не укладывается. Искусству нужно бесконечное число русел.

На формирование новых теорий уходит минимум 10-20 лет. Мир меняется гораздо быстрее, поэтому спасение может быть в формировании множества альтернативных теорий.

А если посмотреть на практическую сторону дела? Электрону (по крайней мере, пока) хватает двух проекций. А сколько их нужно зайцу, чтобы выжить? А человеку — для того же самого? Ответа пока нет. А опыт показывает, что на формирование новых теорий уходит минимум 10-20 лет. Мир меняется гораздо быстрее, поэтому спасение может быть в формировании множества альтернативных теорий.

Близкие траектории как бы притягиваются к одному пучку или руслу. Зная детально одну траекторию, можно много сказать и о других

Но теорию мало создать. Необходимо, чтобы потенциальные ее «потребители» (для социальных теорий это могли бы быть политики и управленцы) смогли без титанических усилий созданное понять и вовремя распознать, что момент ее применимости настал. Поэтому, во-первых, ученым надо учиться делать основные положения и выводы своих теорий максимально простыми и легко проверяемыми, во-вторых, они должны быть изложены общедоступным языком. Осмелимся предположить, что будущее науки связано с широтой кругозора ученых, то есть не с размножением очень специальных журналов и не с электронными публикациями (это всегда сохранится для узкого круга единомышленников), а с возрастанием роли научно-популярной литературы, в которой ученые и журналисты могут писать не для «ближнего», а для «дальнего». Причем ее роль скорее всего изменится качественно — ученые будут писать ее для ученых. Эволюционисты ведь учат, что развитие идет путем превращения побочных форм в основные…

Будем надеяться, что третьей парадигме повезет не меньше, чем первым двум.

Оказалось, что в основе разных явлений лежат одни и те же механизмы, отрицательные и положительные обратные связи. Это позволило понять, как следует строить радиолокационные станции, что происходит при заболеваниях нервной системы, как создавать управляющие структуры, чем мозг отличается от компьютера и множество других вещей. На многие системы оказалось возможным взглянуть как на «черный ящик», который по определенным правилам реагирует на приходящие к нему сигналы. И не так уж важно, находится ли в «ящике» компьютер или подопытное животное, оператор или демон Максвелла.

На первый взгляд принцип дополнительности кажется странным инородным телом, легкомысленно-гуманитарным в стройном здании такой серьезной и солидной науки, как теоретическая физика. Но оказалось, что в одних случаях электрон следует рассматривать как волну и писать одни уравнения, а в других — как частицу и писать другие. Эти описания не вытекают одно из другого, их можно мыслить как разные отражения нашего мира, разные проекции реальности.

Специалистам по прогнозам в разных областях известно, что прогноз возможен далеко не всегда. Например, трехнедельного прогноза погоды, вообще говоря, не существует. Однако, если метеорологу показать некоторую особую погодную ситуацию, сложившуюся над Северной и Западной Европой, он довольно точно расскажет, что будет в ближайшие два месяца. Речь идет о явлении, которое названо в статье «руслами». Близкие траектории как бы притягиваются к некоторому пучку и далее следуют вместе.

Георгий Малинецкий, Алексей Потапов