Институт физических проблем им. П.Л. Капицы,
Институт социально-экономических проблем народонаселения РАН, 2008

В очерке кратко изложена модель роста человечества и обсуждено значение этих результатов для антропологии и истории, экономики и безопасности развития. В основе исследования лежит количественное описания человечества как динамической системы. Её рост и развитие обязано взаимодействию, охватывающее всех людей и возникшее тогда, когда появился человек, одаренный сознанием. Именно развитым сознанием, языком и культурой мы отличаемся от животных, и потому нас в сто тысяч раз больше, чем сравнимых с нами тварей

Светлой памяти Сергея Павловича Курдюмова, ученого и друга

От автора

В очерке кратко изложена модель роста человечества и обсуждено значение этих результатов для антропологии и истории, экономики и безопасности развития. В основе исследования лежит количественное описания человечества как динамической системы. Её рост и развитие обязано взаимодействию, охватывающее всех людей и возникшее тогда, когда появился человек, одаренный сознанием. Именно развитым сознанием, языком и культурой мы отличаемся от животных, и потому нас в сто тысяч раз больше, чем сравнимых с нами тварей.

Модель роста основана на образах физики и неизбежно обращается к математике для описания явлений истории. Она элементарна, и можно только надеяться, что современные обществоведы смогут овладеть математикой в той мере, как и Мальтус, который, готовясь принять сан, занял девятое место на математической олимпиаде Кембриджского университета в 1783 году. В данной статье математические выводы выделены в главу 3 и вполне были бы доступны Мальтусу – автору первой модели роста населения. Однако при обосновании модели необходимы представления нелинейной физики, которые принадлежат уже науке ХХ века.

Связь между ростом населения мира и длительностью развития нельзя понять без учета относительности времени, когда масштаб времени истории сжимается в десятки тысяч раз. Так становится понятным происхождение глобальной демографической революции, которое переживает человечество, как представление о фазовом переходе в сложной системе. С критическим переходом от взрывного роста к постоянной численности связаны наиболее острые вопросы жизни народов, в первую очередь падение рождаемости, глобальная безопасность и развитие общества знания. В современном мире кризис проявился и в том, что экономическое могущество не соответствует управлению нашим развитием на всех уровнях, что видно по расхождению наших дел и мыслей.

В этих исследованиях, обращаясь к росту всего человечества за все времена, неизбежно происходит потеря деталей развития в пространстве и времени, а сами представления лишь приближенно описывают прошлое. Но в то же время, когда происходят такие глубокие изменения в нашей истории, как демографическая революция, необходим новый уровень обобщения и новый синтез. Быть может, поэтому следует обращаться к понятиям наук, самонадеянно называющих себя точными и количественными, для опыта комплексного и междисциплинарного изучения нашего развития. Поэтому автор надеется, что представленный очерк исследований поможет установления понимания между двумя главными силами – силой нашего разума и нашего материального развития, что особенно существенно для России.

Подробности выводов, сводные данные антропологии и истории, ссылки на литературу можно найти в работах автора, указанные в краткой библиографии, а также в докладе “ Global Population Blow — up and After . The Demographic Revolution and Information Society ”, представленный и затем опубликованный Римским клубом.

Представленный ниже текст дает краткое изложение основных результатов, опубликованных в статьях и монографиях автора. Развитие этих исследований было бы невозможным без обсуждений с коллегами из самых разных областей знания. Я обязан А.Г. Вишневскому, который познакомил меня с проблемами и методами демографии. Л.И. Абалкину, В.Л. Макарову, А.Ю. Шевякову, Р.М. Энтову и Фонду Кондратьеву я благодарен за внимание и поддержку со стороны экономистов. Очень существенно было внимание историков В.С. Мясникова и А.О. Чубарьяна, и особенно понимание и поддержка В.С. Стёпина и А.А. Кокошина.

Обсуждение результатов проходило на конференциях и встречах в Московском физико-техническом институте и Московском государственном университете, где я обязан В.А. Садовничему за понимание и поддержку. Очень много для поддержки и развития работ сделал С.П. Курдюмов и коллектив Института прикладной математики им. М.В. Келдыша. Существенно было внимание и уровень обсуждения на заседании Президиума РАН и выступления в университетах Амстердама, Гронингена, Эйндховена, Стокгольма, Петербурга, Дрездена, Котбуса. Выступления в Курчатовском научном центре, Объединенном институте ядерных исследований, Институте демографии Московской высшей школе экономики, ЦЕРНе, Массачузетском технологическом институте, Национальной Лаборатории в Лос Аламосе и Института Санта Фе представили возможность выступить перед аудиторией физиков. Продуктивным было участие в проектах Терра – 2000 и ЮНЕСКО, Пагуошских конференциях и встречах Римского Клуба. Участие в Давосском Форуме, Европейском деловом конгресс и выступление на годичном заседании Дойче Банк, позволили понять интересы деловых кругов. Поддержке ЮНЕСКО, Лондонского Королевского Общества, фондов ИНТАС и РФФИ я обязан на разных этапах работы. Я благодарен Российскому новому университету и ректору В.А. Зернову, Никитскому клубу, который представили уникальную возможность для дискуссий и Московской межбанковской валютной бирже и её Дирекция в лице А.И. Потемкина за неизменное внимание, и помощь со стороны Н.М. Румянцевой.

Я также глубоко благодарен Ж.И. Алферову, К.В. Анохину, М. Аттия, Г.И. Баренблату, В. Вайскопфу, Р. Вайлеру, Н.Н.Воронцову, А.Г.Волкову, О.Г. Газенко, А.В. Гапонову-Грехову, А.А.Галецкому, И.М. Гельфанду, В.Л. Гинзбургу, А.Я. Гольдину, А.А. Гончару, П. Джонстону, И.М. Дьяконову, В.В. Иванову, Б.Б. Кадомцеву, Н.В. Карлову, Н. Кейфицу. А. Кингу, И. Коппену, Ю.Л. Климонтовичу, О.Л. Кузнецову, А.Б. Куржанскому, Е.Н. Куркиной, Г.В. Манелису, Г.Г. Малинецкому, Г.И. Марчуку, Г.А. Месяцу, Н.Н. Моисееву. Ю.С. Осипову, И.В. Перевозчикову, И.Р. Пригожину, Г. Принсу, Л.П. Питаевскому, Ф.-Й. Радермахеру, М. Ризу, Н.М. Римашевской, Д. Ротблату, Ю.А. Рыжову, Д.И. Трубецкову, В.Е. Фортову, А.М. Фридману, Г. Харигелю, Н. Хейфицу, Д. Холдрену, Х. Шопперу, А.-М. Четто, Эль Хасан бин Талалу и А.Л. Яншину за понимание и поддержку.

1. Введение

Исследования по созданию теория роста человечества привели к тому, что была предложена количественная модель нашего роста и развития [1,2,3]. Однако тогда не в полной мере была выяснено, почему эта модель, математические средства которой очень просты, даже элементарны, оказалось столь содержательной и эффективной. Поэтому данная статья посвящена не столько более компактному выводу основных формул, сколько выяснению обстоятельств их соответствия действительности. Это позволит понять пределы применимости модели и той роли, которую играет взрывной характер развития и статистическая природа рассматриваемых явлений. Именно это привело к трудностям в принятии развитого подхода и тех выводов, к которым он приводит, в первую очередь среди демографов.

В основе рассмотрения роста и развития человечества положен подход к населению мира как целого, как развивающейся динамической системы. Однако такой взгляд традиционно отрицался в демографии. Задачу демографии видели в том, чтобы в рамках отдельной страны или региона связать рост населения с конкретными социальными и экономическими условиями. На такой основе уже следовало определять рекомендации по демографической политики. Очевидно, что таким образом  нельзя было определить  общие  для человечества причины роста населения.

Только поднявшись на глобальный уровень анализа, изменив масштаб проблемы, рассматривая все населения мира как единый объект, как взаимосвязанную систему, удалось описать развитие человечества в целом. Именно с таких позиций можно понять глобальный демографический переход, который мы переживаем, и предложить картину нашего развития в обозримом будущем. Такое обобщенное понимание истории оказалось не только возможным, но и очень результативным. Для этого надо было коренным образом изменить метод исследования, точку зрения, как в пространстве, так и во времени, и рассматривать человечество с самого начала своего появления как глобальную структуру, в которой развитие представлено как последовательность фазовых переходов, завершающихся демографической революцией. Тогда причину роста и развития следует искать не в сумме всех действующих факторов, а в том коллективном взаимодействии, которым охвачено человечество. Вместо редукции развития к сумме элементарных процессов мы обратимся к феноменологическому, целостному описанию роста и будем рассматривать человечество как единую, сильно связанную систему, в которой действует общий механизм управляющий развитием. Иными словами, мы обращаемся к методам, основанных на нелинейных представлениях в описании причинных связей.

Следует подчеркнуть, что большинство крупных историков, как Фернан Бродель, Карл Ясперс, Иммануил Валлерштейн, Николай Конрад, Игорь Дьяконов, утверждали, что существенное понимание развития человечества возможно только на глобальном уровне. В значительной мере ими был развит целостный взгляд на нашу историю. Действительно, историческая наука прошла долгий путь, в течение которого историки постепенно шли к поиску тех общих закономерностях, которые определяют рост и развитие человечества. Надо отметить, что эти поиски были не легкими, поскольку, как и в демографии, частные факты и обстоятельства мешали такому общему пониманию, когда во всё увеличивающемся множестве частностей пытались уловить общие законы. Недаром видный экономист Фридрих фон Хаек заметил, что «Распад исследований общества на специализированные дисциплины привел к тому, что все наиболее существенные вопросы пренебрежительно относились к маргиналиям неясной философии развития общества».

Крайним выражением такого редукционизма стал первый доклад Римскому клубу, когда 30 лет тому назад, опираясь на анализ обширных баз данных и компьютерное моделирование, где была сделана попытка описать текущее развитие человечества [15]. С одной стороны так было привлечено внимание к глобальным проблемам, но с другой стороны критика этого подхода показала его ограниченность . Ограниченность не только во времени, но и в тех, по существу линейных моделей, которые были положены в основу этого подхода. В этом отношении существенно замечание американского экономиста, лауреата Нобелевской премии Герберта Саймона что: «Сорок лет опыта моделирования сложных систем на компьютерах, которые с каждым годом становились все больше и быстрее, научил, что грубая сила не поведет нас по царской тропе к пониманию таких систем… Тем самым моделирование потребует обращение к основным принципам, которые приведут нас к разрешению этого парадокса сложности». Данная работа есть ответ на этот вызов.

Мы вернулись к этим проблемам на новом уровне развития математического моделирования, поскольку только так возможно понять природу глобального развития и возникновения мирового демографического кризиса. Помимо фундаментального значения таких работ для понимания развития человечества в целом, такие исследования глобальной истории необходимы и для нашей страны. Благодаря масштабам, истории и разнообразию социальных и экономических условий Россия во многом воспроизводит глобальные процессы. Поэтому для нас так важно понимание процессов развития всего человечества, что таким путем мы обращаемся к российским проблемам в критическую эпоху отечественной и мировой истории. Так развитые

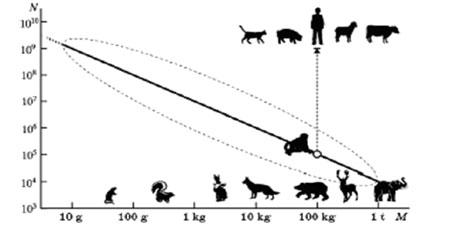
Рис. 1. Численность видов животных на Земле в зависимости от их массы

представления ставят вопрос об их влиянии на наше видение прошлого, на антропологию и исторические науки. В тоже время эти представления затрагивают вопросы экономики и мировой безопасности, так существенные для современности.

2. Моделирование глобального роста человечества

В соответствии с данными антропологии предки человека появились в Африке более миллиона лет тому назад, когда их численность была порядка ста тысяч. С тех пор человек начал расселяться по всему земному шару, а число людей постепенно возросло в сто тысяч раз – до современных миллиардов. Современный человек Homo sapiens несомненно представляет один вид, с одним числом хромосом, а представители разных рас могут скрещиваться между собой. Но ни один вид сопоставимых с нами по питанию и биологии животных никогда не развивался так стремительно: например, и сейчас в России живет около ста тысяч медведей или волков, и столько же крупных обезьян в тропических странах. Такие популяции занимают ограниченный ареал, и их численность определяется динамическим равновесием с окружающей природой. Только домашние животные умножили свою численность далеко за пределами своих диких собратьев: число голов крупного рогатого скота в мире превышает 2 млрд. Именно численность людей выделяет нас среди других видов и это вынуждает некоторых, ограниченных как умом и знаниями людей, обращаться к представлениям о не-эволюциионном происхождении человека, поскольку где недостающее звено между обезьяной и человеком – The missing link between man and ape ?

На эту загадку в эволюции человека предлагают ответ последние исследования, проведенные методами молекулярной биологии. По-видимому, критическим событием стало появление мутации гена HAR 1 F , который определяет рост мозга человека на 5 – 9 неделе развития эмбриона. Поэтому есть основания считать, что такое внезапное

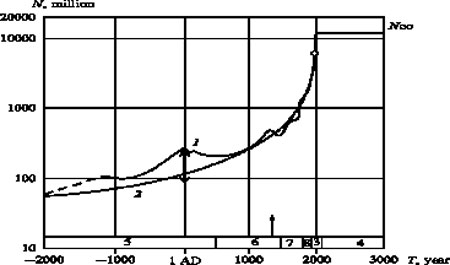
Рис.2. Население  мира  от  2000г. до Р.Х.  до  3000г. 1 – население мира от 2000г. до Р.Х. 2 – взрывной режим с обострением численности населения мира. 3 – демографический переход,  4 – стабилизация населения, 5 – Древний мир, 6 – Средние века,   7 – Новая история и 8 – Новейшая история, ^ – пандемия чумы 1348г., ¦ – разброс данных.

точечное изменение в геноме наших далеких предков 7 – 5 млн. лет тому назад могло привести к скачку в организации мозга. Это стало причиной развития социального сознания и культуры, приведшие к величайшему численному росту человечества. Так, вследствие этой мутации, после длительной эпохи антропогенеза появились речь и язык, человек овладел огнем и технологией каменных орудий. С тех пор биологически человек изменился мало, однако наше социальное развитие был стремительно. Поэтому понимание этого процесс так значимо для нас сегодня, когда выяснилось, что именно нелинейная динамика роста населения человечества, подчиняющаяся собственным внутренним силам, определяет не только наше взрывное развитие, но и его предел. Именно это позволило сформулировать феноменологический принцип демографического императива, вследствие которого рост определяется самим населением мира и развитием его сознания, в отличие от популяционного принципа Мальтуса, когда ресурсы ограничивают предел роста.

Для того чтобы пояснить суть проблемы, обратимся к росту численности и развития человечества на протяжении последних тысяч лет. Исходным было наблюдение, отмеченное рядом исследователей, что рост населения Земли подчиняется универсальной закономерности гиперболического роста. На графике Рис. 2 численность населения N представлена в логарифмическом масштабе, а течение времени Т – на линейном шкале в котором также указаны основные периоды мировой истории. Если население мира росло бы экспоненциально, то на этой сетке такой рост отображался бы прямой. Однако для человечества рост в начале проходил очень медленно. Так, первый миллиард появился за миллион лет самоподобного роста,

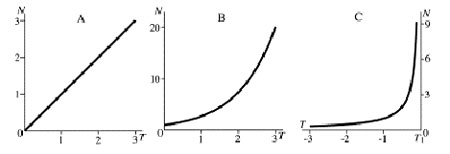
Рис. 3. Линейный р ост – А, экспоненциальный р ост – В и гиперболический р ост – С

проходившего по неизменному закону, только к началу XIX века. Но уже в 1930 году население мира достигло 2 млрд., все ускоряется по мере приближения к эпохе 2000г. Эта картина внезапного взрыва роста приводила многих в недоумение, однако она непосредственно является следствием нелинейности роста.

Задача же модели и теории гиперболического роста состоит в установлении природы и пределов этой картины развития. В итоге, опираясь на статистические принципы физики, в элементарных выражениях удалось описать динамически автомодельное развитие человечества за миллионы лет – от возникновения человека до наступления демографического перехода и далее в предвидимое будущее. Секрет гиперболического, взрывного развития состоит в том, что скорость роста пропорциональна не первой степени численности населения, как у экспоненциального роста, а второй степени – квадрату численности населения мира.

Рассмотрим примеры роста, показанные на Рис. 3. Таким является линейный рост А, пропорциональный времени и скорость которого постоянна. Очевидно, что в этом случае нет характерного времени роста. Экспоненциальный рост В пропорционален уже самому населению и этим свойством не обладает, поскольку в этом случае есть характерное время удвоения . В математике обычно принято обращаться ко времени экспоненциального роста системы в раз, где – основание натуральных логарифмов, а время удвоения на 30% меньше .

Наконец, обратимся к росту происходящему пропорционально квадрату населения , который приводит к гиперболическому графику роста С и для которого также нет характерного времени роста. Этот закон роста представляет для нас основной интерес. Действительно, рядом авторов (Макендрик, Форстер, Хорнер,) было обращено внимание на то, что данные для населения мира за несколько веков с удивительной точностью описываются формулой:

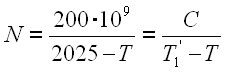(1)

где млрд. – постоянная с размерностью [человек годы], а время выражено в годах от Р.Х. И.С.Шкловский в конце 6 издания замечательной книге «Вселенная жизнь, разум» также обратился к этой формуле [20]. Он пришел к выводу, что рост определяется социальными, а не биологическими факторами, которые и ограничат рост. Заметим, что постоянство этого закона роста поразительно и в пределах той точности, с которой нам известны оценки населения в прошлом, он соблюдается при увеличении населения Земли в десятки тысяч раз. Так описывается развитие человечества по существу с самого момента появления Homo habilis полтора миллиона лет тому назад, на что не было обращено должного внимания.

В демографии выражение (1) никогда всерьез не рассматривалось по двум причинам. Во первых, оно обращается в бесконечность по мере приближения к 2025 году. Во вторых, в демографии считалось беспредметным рассматривать все население Земли не иначе, как арифметическую сумму населения отдельных стран, поскольку задачей демографии является объяснение роста в рамках конкретных социальных и экономических условий, которые не возможно сформулировать для всего населения мира. Более того, это выражение приводит к трудностям и в прошлом. Так 20 миллиардов лет тому назад должно было бы уже быть десять человек, несомненно, космологов, наблюдающих и обсуждающих возникновение Вселенной!

Однако мы будем рассматривать не как эмпирическое обобщение данных, а как выражение физической закономерности и математически содержательную формулу. Она описывает рост населения как самоподобный процесс, следующий по гиперболической траектории, имеющие особенность в то критическое мгновение 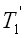, когда обращается в бесконечность. Именно в этой сингулярности состоит главная привлекательность этой формулы, несмотря на то неприятие, которое в прошлом такие выражения вызывали у некоторых математиков. Однако в современной математике подобные процессы с обострением подробно изучены и нашли обширные приложения в теории взрывных процессов, ударных волн и физике фазовых превращений [21, 22].

Таким образом в основе роста человечества лежит коллективное взаимодействие, аналогичное взаимодействию Ван дер Вальса в неидеальном газе или плазме, которое изучено в физике конденсированного состояния и кинетике нелинейных явлений в синергетике. В таких системах с сильной связью взаимодействующих частиц возникают коллективные степени свободы, определяющие их рост и развитие. Анализ гиперболического роста человечества, связывающий численность и рост человечества с его развитием позволил предложить кооперативный механизм развития, когда мерой развития является квадрат численности населения мира. Это позволяет по-новому представить глобальную историю человечества. Она начинается с особенности появления сознания и завершается демографическим взрывом – режимом с обострением и фазовым переходом при резким изменении всего хода нашего развития. Эти понятия принадлежат физике сложных систем. Теперь они применяются к человечеству и служат основаниям для новых количественных результатов и поучительных аналогий. Так этот опыт междисциплинарного исследования расширяет наше представлений о росте человечества за всю эпоху его развития.

Интерпретация развития основана на предположении, что коллективное взаимодействие определяется механизмом распространения и размножения обобщенной информации, происходящее в человечестве, как глобальном сетевом информационном сообществе. Этот рост определялся самосогласованным системным развитием, а движущим фактором автомодельного развития оказываются связи, охватывающее все человечество эффективным информационным полем. На основе такого феноменологического подхода впервые удалось предложить полную теорию роста и количественно описать важнейшие явление развития человечества. Однако, обращаясь к понятиям физики и языку математики существенно привести эти представления в соответствие с образами и понятиями историков. Так н а учет разных временных масштабов процессов в исторических науках указывал Бродель: «Историки в последнее время стали выделять это различие в образах временных структур и связей. Первые относятся к долговременным и вторые к кратковременным сущностям». Это указывает на общность видения явлений у историков и физиков.

Как поучительный пример кинетики таких процессов приведем атомную бомбу, в которой в результате разветвленной цепной реакции происходит ядерный взрыв. Квадратичный рост населения нашей планеты указывает на то, что аналогичный процесс протекает в человечестве, только гораздо медленнее, но не менее драматично, когда информация в результате цепной реакции умножается на каждом этапе роста, определяя темп развития во всем мире.

Я хорошо помню, как это было осознано во время моего доклада в Институте прикладной математики им. М.В.Келдыша на семинаре Сергея Павловича Курдюмова. Им и его коллегами для проблематики режимов с обострением развиты мощные математические методы и этому посвящена громадная литература. Более того,

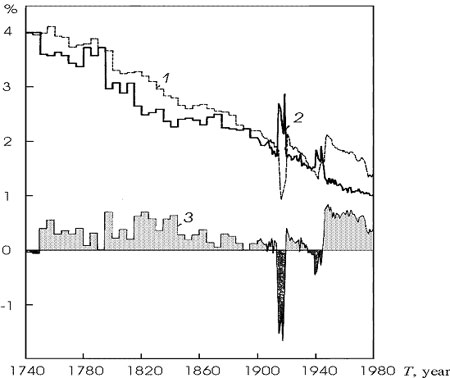
Рис. 4. Рост населения и демографический переход во Франции [11].

Курдюмов и его сотрудники видели в этой области математики обоснование тех подходов к изучению сложных систем, которые были развиты немецким физиком Хакеном [17]. В синергетике, в частности разный временной масштаб процессов лежит в основе приближенных асимптотических методов при рассмотрении сложных систем.

Если экспоненциальный рост определяется только индивидуальной способностью человека к размножению, то рост человечества происходит в результате коллективного механизма роста. Именно в этом состоит качественное отличие человека от всех остальных животных, управляемых врожденными инстинктами, а не системой приобретенных и развивающихся знаний. Таким образом, рост и развитие коренным образом отличается тем, что благодаря разуму и сознанию, его культурой и развитой системой передачей информации как вертикально, из поколения в поколение, так и в пространстве – горизонтально, человечество в среднем устойчиво следует по статистически детерминированному пути автомодельного роста. Это происходит вплоть до демографической революции, когда рост численности прекращается.

Для установления поведения роста человечества вблизи сигулярности роста следует обратиться к явлению демографического перехода. Переход состоит в резкой смене роста на режим стабилизации населения. Он был открыт первоначально для Франции французским демографом Адольфом Ландри, который писал: «В XVIII веке Франция пережила не только свою великую политическую революцию, которая совершилась в 1789 году, но и демографическую революцию. Политическая революция от¬ мечена такими яркими событиями, как штурм Бастилии или уничтожение привилегий; в течение нескольких лет многое не¬ обратимо изменилось

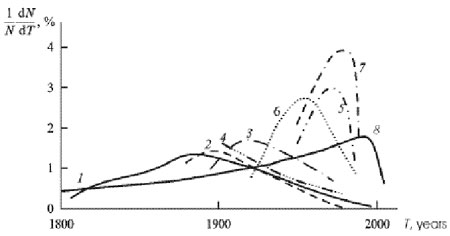
Рис . 5. Демографический переход в разных странах. Графики сглажены и рост дан в % в год.
1 – Швеция, 2 – Германия, 3 – СССР, 4 – США, 5 – Маврикий, 6 – Шри Ланка, 7 – Коста Рика и 8 – для мир в целом [11]. Н а этом графике видно как происходит формирование глобального перехода. Если переход в Швеции и во Франции занял 160 лет, то чем позднее он происходит, тем переход острее.

и сменило существующий порядок. Но ни¬чего столь же сенсационного, что отметило бы наступление дру¬ гой революции не произошло. Ее развитие было незаметным и относительно медленным. Тем не менее, она не в меньшей сте¬пени является революцией, поскольку тогда, когда происходит изменение режима, революция и происходит. Это верно в демо¬графии, как и любой другой области. Внезапность изменений не является обязательной. Действительно, говоря о демографичес¬ кой революции, при которой происходит смена неограниченного воспроизводства на ограниченное, есть все основания придержи¬ ваться данного определения, без каких-либо добавлений».

Для отдельных стран переход показан на Рис. 5 и для населения мира на Рис. 6. Если демографы обычно исследовали демографический переход в масштабе страны, то нам гораздо ближе определение Ландри демографического перехода как революции, но уже рассматриваемого как глобальное явление. Теория процессов развития и роста дана ниже и может быть опущена читателем при первом чтении.

3. Математическая модель роста населения Земли

Население мира N ( T ), будет описываться функцией от времени T , определяющее состояние демографической системы Земли. Тогда ведущей переменной, параметром порядка, подчиняющей все остальные переменные, станет полное число людей N . Таким образом, в этом приближенном функциональном соотношении не учитывается распределение населения по нашей планете, ни его экономическое и возрастное состояние или расовой и национальный состав. Сам процесс роста также будет рассматриваться на значительном интервале времени T – большом числе поколений. Иными словами мы будем рассматривать усредненные значения переменных и усредненные функции, чем, в частности, вносится в уравнения память о прошлом, определяемая временем усреднения переменных.

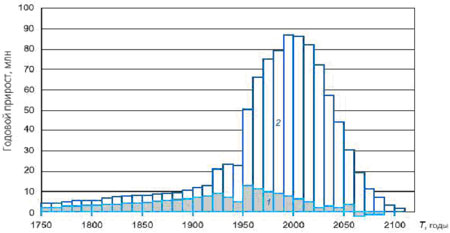
Рис. 6. Мировой демографический переход 1750 – 2100гг. Данные ООН.

Годовой прирост, усредненный за декады. На рисунке видно уменьшение скорости роста при мировых войнах и демографическое эхо войны в начале XXIв. 1 – развитые страны и  2 – развивающиеся страны.

Такое выделение главных переменных N и T и их усреднение характерно для системного подхода. Оно получило развитие в синергетике и лежит в основе асимптотических методов, развитых для решения задач большой сложности, появляющихся при рассмотрении систем со многими степенями свободы. Существенно то, что эти переменные, которые представляют все социально значимые факторы по возрастам и полу, образования, развития, доходов и т.д. описываются статистическими распределениями. Когда рассматриваются такие многофакторные проблемы, то в известных пределах можно полагать, что развитие системы статистически стационарно и потому происходит динамически самоподобно. Это сильное предположение означает, что остаются неизменными пропорции между относительными изменениями времени и населения.

Смысл этой основной гипотезы автомодельности состоит в том, что утверждается постоянство относительной скорости изменения системы, аналогично принципу инерции. В таком случае можно показать, что такой самоподобный рост должен описываться степенной функцией без характерного параметра, такого как масштаб времени. Такие процессы обладают масштабной инвариантностью – скейлингом, аналогично развитой турбулентности в потоке жидкости. Эти понятия мало знакомы историкам и обществоведам, однако подобные представления должны помочь в расширении тех образах, в которых мы описываем исторический процесс. Сделанные предположения упрощают задачу, сводя все к одной переменное N ( T ), рост которой зависит от состояния самой системы. Формула (1), как степенная функция, обладает такой масштабной инвариантностью – отсутствием собственного масштаба времени, свойство открытое еще Эйлером и указывающее на автомодельность роста. Но в нашей задаче роста населения эта формула является лишь первым приближением. Как асимптотическое выражение оно ограничено областью применения, и задача теории в первую очередь состоит в установлении этих пределов как вблизи особенности, когда эта функция устремляется в бесконечность, так и в далеком прошлом, когда ее уменьшение происходит слишком медленно.

Чтобы описать переход следует учесть время, характеризующее внутренние процессы как продолжительность жизни человека и время его репродуктивной способности. Это те факторы, которые при прохождении через демографический переход ограничивает скорость роста по мере приближения к моменту, когда скорость роста приближается к своему пределу. При этом независимой переменной становится численность населения N , а не время Т.

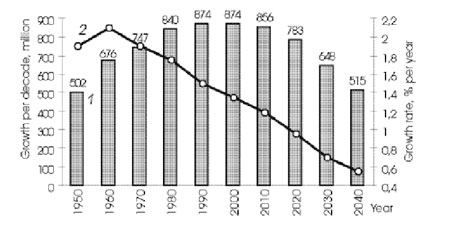
Рис. 7. Мировой демографический переход вблизи 2000 года. Данные ООН.
1 – абсолютный прирост населения осредненный за декаду, млн. 2 – относительный прирост % в год.

Для этого следует продифференцировать (1) и получить выражение для скорости роста в зависимости от времени:

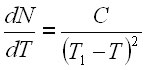(2)

а затем ввести в это расходящееся выражение характерное время , ограничивающее скорость роста:

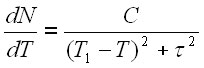(3)

Этот прием может показаться произвольным шагом, однако полученное выражение очень хорошо описывает глобальный демографический переход и отвечает тем методам в теоретической физике, которые развиты для регуляризации расходимости, с которой мы столкнулись при анализе демографического перехода. Интегрируя (3), мы получим выражение для описания перехода:

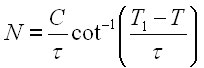(4)

При обработки последних данных демографии получены уточненные значения постоянных, когда критический год сместился к 1995г., вместо 2000г., что и учтено в последующих вычислениях:

,

года.,

лет и безразмерное число

Из-за введения конечного полюс в сдвигается к новому значению г., которое и принято в выражении (4) описывающей демографический переход и рост за пределы особенности при и сравнении расчетов с данными демографии. См. Таблицу 1, Рис. 6,7 и 9.

В недалеком прошлом выражение (4) асимптотически непосредственно переходит в автомодельный гиперболический рост. Однако в очень далеком прошлом скорость роста должна быть ограничена снизу. Этого предположения достаточно для того, чтобы приписать в далеком прошлом линейный рост, при котором в первом приближении скорость роста не может быть меньше появления одного гоминида за характерное время . В результате, в течение эпохи антропогенеза численность населения становится порядка ста тысяч. В популяционной генетике это число характерно для стабильного вида, биологически подобному человеку. Именно тогда начинается квадратичный рост, обязанный информационной природе развития, который с тех пор станет доминирующим фактором.

Численность человечества в этот момент представляет большой интерес, и потому я обратился к знаменитому французскому антропологу, профессору Коллеж де Франс Ив Коппену с вопросом: сколько тогда жило людей? Его ответ был краток и точен – сто тысяч. Оценка основана на наблюдении, что тогда на востоке и юге Африки было порядка тысячи больших семей, по сто человек в каждой, что не противоречит оценкам других авторов для этого существенного момента в истории человечества.

Величина К определяет не только масштаб численности человечества в начальную эпоху роста, но также дает оценку численности когерентной группы людей или племени, самодостаточного населения малого города или масштаб такой группы в мегаполисе. Так в Москве, при населении около 10 миллионов город разбит на сто административных округов по сто тысяч каждый. Как большой параметр задачи постоянная К определяет все соотношения между населением и длительностью процессов роста, а значительная величина константы К приводит к высокой эффективности асимптотических решений. Таким образом скорость роста населения Земли в эпоху В определяется автономном дифференциальным уравнением в котором время не входит в его правую часть:

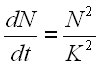, (6)

когда и отсчитываться от времени прохождения через демографический переход и выражено в единицах характерного времени . Формула роста (6) выражает природу того коллективного нелинейного взаимодействия, которое ответственно за рост человечества в эпоху его взрывного развития. В этом уравнении для усредненных переменных Т и N скорость роста приравнена к развитию, которое равно квадрату численности населении мира, как выражение меры системной сложности населения планеты. Его также можно рассматривать как результат парного взаимодействия N человек, или же как некое эффективное поле, феноменологически определяющее рост.