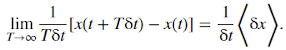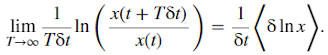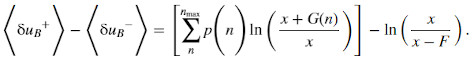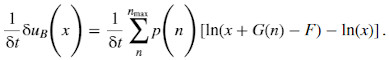ABSTRACT
Gambles are random variables that model possible changes in wealth. Classic decision theory transforms money into utility through a utility function and defines the value of a gamble as the expectation value of utility changes. Utility functions aim to capture individual psychological characteristics, but their generality limits predictive power. Expectation value maximizers are defined as rational in economics, but expectation values are only meaningful in the presence of ensembles or in systems with ergodic properties, whereas decision-makers have no access to ensembles, and the variables representing wealth in the usual growth models do not have the relevant ergodic properties. Simultaneously addressing the shortcomings of utility and those of expectations, we propose to evaluate gambles by averaging wealth growth over time. No utility function is needed, but a dynamic must be specified to compute time averages. Linear and logarithmic “utility functions” appear as transformations that generate ergodic observables for purely additive and purely multiplicative dynamics, respectively. We highlight inconsistencies throughout the development of decision theory, whose correction clarifies that our perspective is legitimate. These invalidate a commonly cited argument for bounded utility functions.
Over the past few years, we have explored a conceptually deep, simple, change of perspective that leads to a novel approach to economics. Much of current economic theory is based on early work in probability theory, performed specifically between the 1650s and the 1730s. This foundational work predates the development of the notion of ergodicity, and it assumes that expectation values reflect what happens over time. This is not the case for stochastic growth processes, but such processes constitute the essential models of economics. As a consequence, nowadays expectation values are often used to evaluate situations where time averages would be appropriate instead, and the result is a “paradox,” “puzzle,” or “anomaly.” This class of problems, including the St. Petersburg paradox and the equity-premium puzzle, can be resolved by ensuring the following: the stochastic growth process involved in the problem needs to be made explicit; the process needs to be transformed to find an appropriate ergodic observable. The expectation value of the new observable will then indeed reflect long-time behavior, and the puzzling essence of the problem will go away. Here we spell out the general recipe, which we phrase as the solution to the general gamble problem that stood at the beginning of the debate in the 17th century. We hope that this recipe will resolve puzzles in many different areas.
I. PRELIMINARIES
Whether an observable possesses this property is crucial when assessing the significance of its expectation value. We will refer to observables with this property as “ergodic observables.”
Gambles are the formal basis of decision theory. Decision theory studies mathematical models of situations that create an internal conflict and necessitate a decision. For instance, we may wish to model the situation of being offered a lottery ticket. The conflict is between the unpleasant certainty that we have to pay for the ticket, and the pleasant possibility that we may win the jackpot. It necessitates the decision whether to buy a ticket or not. Although economics deals with many types of decisions, not all of which are monetary, the quantitative treatment of the gamble problem is central to many branches of economics including utility theory, decision theory, game theory, and asset pricing theory which in turn informs macroeconomics, as has been argued convincingly.2
We will be dealing with mathematical models but use a common suggestive nomenclature. In this section, we write in small capitals those terms of everyday language that in the following will refer to mathematical objects and operations.
A gamble is a set of possible net payouts D(n) with associated probabilities p(n), where n is an integer designating an outcome. For convenience, we order outcomes such that D(n+1)>D(n). Different gambles are compared, the decision being which to subject one’s wealth to, and more generally to what extent.
Gambles are versatile models, useful to describe a number of real-world prospects. An insurance contract may be modeled as a gamble, as may an investment. Lotteries are important in the historical development of decision theory. Here, possible prizes G(n) are purchased for a ticket fee, F, leading to possible net payouts, D(n)=G(n)−F, which are negative up to some value of n and then positive. This creates a decision problem when comparing to the option of doing nothing: the certain unpleasant prospect of losing the ticket fee has to be weighed against the uncertain prospect of winning one of the nmax possible prizes.
II. OUTLINE
Section III is a modern treatment of the problem, using dynamics, that is, we use information about temporal behavior, not exclusively measure-theoretic probabilistic information. Expectation values play a central role in economics, essentially for two reasons. First, the expectation value of any observable is, by definition, the average over N instances of the observable, in the limit N→∞. It can therefore be relevant for a member of a large resource-sharing group. Decision theory, however, is concerned with individuals, not with groups, wherefore we disregard this first possible reason for using expectation values. Second, an observable may have the ergodic property mentioned in Section I, in which case it is informative of what happens to an individual over time. We are concerned with the conditions under which this second reason for using expectation values is relevant.
The two key quantities in our treatment are the expected rate of change in wealth, 
, for additive dynamics, and the expected exponential growth rate of wealth, 
, for multiplicative dynamics. Both quantities were suggested as criteria to evaluate a gamble, by Huygens3 and by Laplace,4 although their dynamic significance was overlooked, and time scales δt were usually omitted and implicitly set to 1.
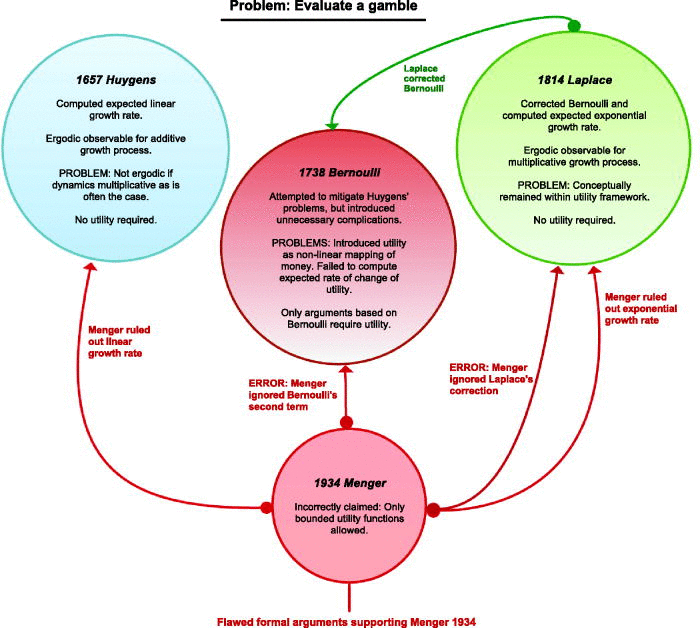
Section IV discusses the complicated historical development of these two criteria, which we now briefly summarize. It is a partial explanation of the fact that this perspective has lain hidden from view, despite its otherwise implausible problem-solving power, and the availability of its conceptual building blocks for more than 100 years now. It is necessary to re-tell the history of the problem because of an important misconception that forbids the modern perspective.
Bernoulli5 suggested a quantity similar to the exponential growth rate and called it a “moral expectation,” interpreting the logarithm in the exponential growth rate as a psychological re-weighting that humans apply to monetary amounts. This presented a very simple criterion—maximizing the expected exponential growth rate—in a very complicated way. Laplace4 corrected Bernoulli formally, though not conceptually, writing down exactly the expected exponential growth rate, though not pointing out its dynamical significance. Menger6 did decision theory a crucial disservice by undoing Laplace’s correction, adding further errors, and writing a persuasive but invalid paper on the subject that concluded incorrectly—in the language of utility theory—that only bounded utility functions are permissible. This forbade the use of either of the dynamically sensible quantities because—forced into the framework of utility theory—the expected rate of change in wealth corresponds to a linear (unbounded) utility function, and the expected exponential growth rate corresponds to a logarithmic (unbounded) utility function.
That unbounded utility functions are not allowed became an established result. We ask here why we cannot use unbounded utility functions, and find no good reason. The arguments for the boundedness of utility functions that we found are not scientifically compelling. A visual representation of the convoluted history of the problem is shown in Fig. 1.
FIG. 1. History of the classic decision theory problem of evaluating a gamble. The two physically meaningful solutions are on the left and right of the figure. Multiplicative wealth models predict qualitative behavioral patterns—such as risk aversion—that additive wealth models do not predict. In this sense, Laplace’s Criterion is often more relevant, especially when changes in wealth δx are of similar scale as wealth x itself. Problematic aspects are color-coded in red.
We conclude in Section V that the modern dynamic perspective is legitimate and powerful. Conceptually, its power derives from a new notion of rationality. Many reasonable models of wealth are non-stationary processes. Observables representing wealth then do not have the ergodic property of Section I, and therefore rationality must not be defined as maximizing expectation values of wealth. Rather, we propose as a null model to define rationality as maximizing the time-average growth of wealth. This can be done by first converting the non-ergodic processes into stationary independent increments per time unit and then maximizing expectation values of these (identical to their time averages because these observables do have the ergodic property of Section I). These observables are growth rates, and their definition is dictated by the dynamics of the wealth model. Because the gamble problem is phrased without reference to possible causes of the changes in wealth it is entirely general, wherefore our work resolves a host of more specific problems in economics, such as the leverage problem,7 the 300-year-old St Petersburg paradox,8 and the equity-premium puzzle.9 The requirement of boundedness for utility functions is both unnecessary and detrimental to the formalism of decision theory. Our analysis of the history of the problem removes this unnecessary obstacle in the way of using physically sensible criteria in decision theory.
III. THE DYNAMIC PERSPECTIVE
In order to evaluate a gamble, we ask: How are the dynamics that the gamble is part of to be modeled? In the examples below, an answer to this question allows us to identify stationary independent increments, i.e., to construct an ergodic observable, whose expectation value reflects the behavior over time. Without an answer, the problem is underspecified and cannot be resolved without further assumptions, for instance about human psychology.
Requesting the specification of a dynamic exposes as underspecified the original set-up of many problems in economics. Economics treats randomness in a purely measure-theoretic way: possible outcomes are given weights (measures or probabilities), and the overall quality of a gamble is a weighted average over outcomes, as if all possibilities were materializing simultaneously with different degrees of reality. Modern perspectives on randomness actively downplay the importance of the specific model of measure theory, and emphasize the need to place the aim of the theory above the conditions imposed by a specific axiomatization. Thus, Gell-Mann and Hartle10 demonstrated that probabilities beyond the interval [0,1] are useful in quantum mechanics, and Tao11 pointed out the importance of invariance under extension of the sample space. In our case, we argue that a dynamic is needed in addition to the random variable, turning the gamble into a stochastic process. Dynamics means repetition, and requiring the specification of a dynamic is requiring the admission that we live through time, not in a superverse of parallel worlds with which we can share resources.
Gambles are often treated in economics as so-called one-shot games, meaning that they are not part of any dynamic and are assumed to reside outside of time, an assumption that is difficult to describe: “it’s more or less impossible to consider any gamble as happening outside of time” [Ref. 12, p. 3]. The one-shot setup seems ill-conceived to us, and the methods we propose produce little insight into the situations it may represent. It is ill-conceived because any gamble affects what we may be able to do after the gamble. If we lose our house, we cannot bet the house again. The typical decision problem only makes sense in the context of a notion of irreversible time and dynamics—we cannot go back in time after the gamble, and our future will be affected by the decisions we make today. One situation that may be represented by a one-shot game is a bet on a coin toss after which the player (who does not believe in an afterlife) will drop dead. Our methods are not developed for such a-typical cases.
A. Additive repetition
Treating D(n) as a (stationary) random variable, repetition of a gamble may mean different things. First, a gamble may be repeated additively, so that the wealth after T rounds of the gamble is
(1)
where nτ labels the outcome observed in the τth round of the gamble.
x does not have the ergodic property of Section I: the expectation value is not constant in time, ⟨x(t+Tδt)⟩=x(t)+T⟨D⟩; the finite-time average, 
, does not converge to the expectation value but rather is a random variable whose distribution broadens indefinitely as T→∞. Averaging N realizations of x(t) over a large ensemble (N→∞) is not equivalent to averaging x(t) over a long time interval Tδt (where T→∞).
An ergodic observable for Eq. (1) exists in the additive changes in wealth, x(t+Tδt)−x(t), whose distribution does not depend on t. They are stationary independent increments for this dynamic. The finite-time average of the rate of change in wealth converges to the expectation value of the rate of change with probability one,
(2)
The expectation value, by definition, is identical to the ensemble average,
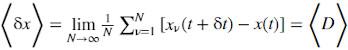, where xν(t+δt) are different parallel realizations of wealth after one round of the gamble.
This explains Huygens’ Criterion: under additive dynamics as in Eq. (1), the rate of change in wealth is an ergodic observable, and he who chooses wisely with respect to its expectation value also chooses wisely with respect to the time average.
For the specific dynamics of Eq. (1), an analysis of this particular observable using our perspective will agree with an analysis using the economics concept of rationality. This is not the case for other observables—Huygens’ Criterion defines something very special: an ergodic observable on a non-ergodic wealth process.
The simplicity of additive dynamics comes at a cost of realism. For instance, it implies that possible changes in wealth are not affected by the current level of wealth. The millionaire and the penniless are modeled as having equal chances of increasing their respective wealths by $10,000. For small gambles (D≪x), this linear approximation can be valid (the chances of gaining at least $0.01 may really be similar), and indeed the use of Huygens’ Criterion emerged from considerations of recreational gambling where an insignificant amount is bet on a game of dice.
B. Multiplicative repetition
A gamble may also be repeated multiplicatively. To simplify notation, we define per-round growth factors 
where t0 is the time just before the first round of the gamble. These inherit their stationarity and independence from D. In this case,
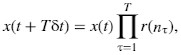(3)
which may be re-written as
(4)
x again lacks the ergodic property of Section I: the expectation value is not constant in time, ⟨x(t+Tδt)⟩=x(t) exp(Tln⟨r⟩); the finite-time average does not converge to the expectation value but rather is a random variable whose distribution is not stationary. Again, averaging many realizations of x(t) over a large ensemble (N→∞) is not equivalent to averaging x(t) over a long time interval (T→∞). Crucially, and in contrast to the additive dynamic (Eq. (1)), additive changes in wealth are not ergodic either. The construction of an ergodic observable now requires a non-linear transformation.
An ergodic observable for Eq. (3) exists in the relative changes in wealth, 
whose distribution does not depend on t. Increments in the logarithm of x are now stationary and independent. The finite-time average of the rate of change in the logarithm of wealth, i.e., the exponential growth rate, converges to the expectation value of the rate of change in the logarithm with probability one,
(5)
The expectation value, by definition, is identical to the ensemble average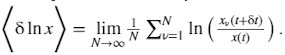 
This explains Laplace’s Criterion: under multiplicative dynamics, the rate of change in the logarithm of wealth is an ergodic observable, and he who chooses wisely with respect to its expectation value also chooses wisely with respect to the time average. Multiplicative repetition is exemplified by geometric Brownian motion, the most influential model in mathematical finance.
Multiplicative repetition represents important qualitative aspects of real wealth processes in a different way than additive repetition. For instance, under multiplicative repetition the likelihood of a $10,000 increase in wealth is no longer independent of initial wealth. Instead of modeling the millionaire and the penniless as having equal chances of gaining $10,000, multiplicative repetition models them as having equal chances of increasing their respective wealths by 1%. Multiplicative repetition treats zero wealth as a special state, resembling a no-borrowing constraint: betting more than we have can have qualitatively different consequences from betting less than we have. Another important, subtle, and more realistic property of multiplicative repetition is this: time-average growth is impaired by fluctuations. Unlike under additive repetition, the introduction of fluctuations that do not affect the expectation value does reduce the growth rate that is observed with probability one over a long time. In the sense that some dynamical models are more realistic than others, reality imposes a dynamic and corresponding ergodic growth rates on the decision-maker. We may choose which gamble to play but we do not get to choose the mode of repetition.
Yakovenko and Rosser13 discussed in detail the regimes of applying additive and multiplicative models of monetary wealth. The gamble problem deals with monetary wealth, but it is useful to look beyond this domain. “Living systems […] give rise to organisms like themselves” [Ref. 14, p. 5]. Life self-reproduces, is multiplicative. Hence, multiplicative models capture emergent properties of living entities that additive models fail to capture. An example is cooperation and the formation of social structure.15
Equipped with modern tools, we have no need for the concept of utility. The general gamble problem can be resolved without it, as can—of course—special cases, such as the 300-year-old St Petersburg paradox.7
Common error
Prominent texts in decision theory make incorrect statements about the equality of expectation values and time averages, as for instance in the following passage: “If a game is “favorable” from the point of view of the expectation value and you have the choice of repeating it many times, then it is wise to do so. For eventually, your amount of money and, consequently, your utility are bound to increase (assuming that utility increases if money increases),” [Ref. 16, p. 98].
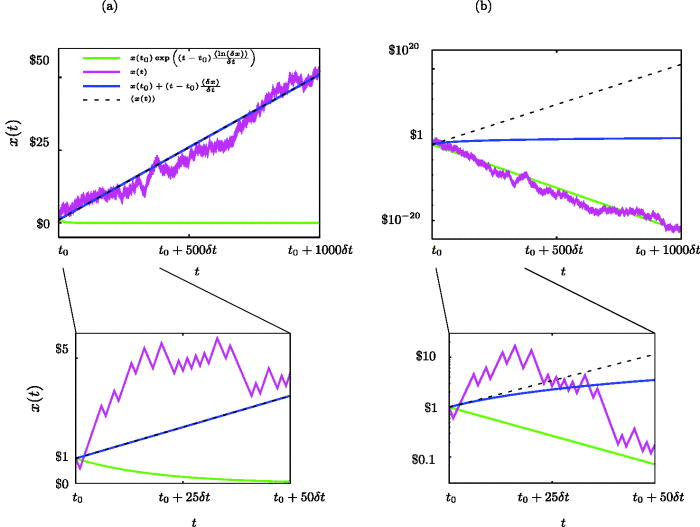
This statement by Chernoff and Moses is not true if “favorability” is judged by an observable that does not have the ergodic property of Section I. The general falsity of their statement is evident in panel (b) of Fig. 2, an example of the multiplicative binomial process, studied in detail by Redner.17 Here, x is not ergodic, and the game is “favorable from the point of view of the expectation value” of x, but it is certainly not wise to repeat it many times. We will use italicized text in boxes to highlight errors and weaknesses in arguments that are commonly believed to be valid.
FIG. 2. Assume initial wealth x(t0)=$1 and toss a fair coin. If tails show (n=1), x decreases to x(t0+δt)=$0.60. If heads show (n = 2), x increases to x(t0+δt)=$1.50. The gamble is repeated (a) additively, linear plot, and (b) multiplicatively, log-linear plot (zoom-ins below the main panels). For clarity, the same sequence of heads and tails is used in both plots, and the color-codings are identical. A typical trajectory is shown (magenta lines). Under (a), the expectation value of x (dashed line) grows in time with the expected rate of change (ergodic observable for this dynamic, blue line), and a trajectory growing exponentially at the expected exponential growth rate (green line) does not describe the long-time behavior. Under (b), the expectation value of x grows exponentially but has nothing to do with the long-time behavior—x typically decays exponentially in this case, following the expectation value of the exponential growth rate (ergodic observable for this dynamic). The probability distribution of x is concentrated near the green line at any t, while a small number of a-typical trajectories let the mean grow along the dashed line. Linear growth in time at the expected rate of change in x does not describe the long-time behavior.
IV. HISTORICAL DEVELOPMENT OF DECISION THEORY
In this section, we relate the modern treatment of the gamble problem to classic treatments and highlight common misconceptions as well as inconsistencies within the classic view. Aspects of this history, which are included here for completeness, have been discussed previously.8 Menger’s ill-conceived rejection of unbounded utility functions was discussed by Peters.18 Its treatment here is briefer and more accessible to those unfamiliar with Menger’s original text.
A. Pre-1713 decision theory: Expected wealth
Following the first formal treatment by Fermat and Pascal19 of random events, it was widely believed that gambles are to be evaluated according to the expected rate of change in wealth. To give it a label, this criterion may be attributed to Huygens,3 who wrote “if anyone should put 3 shillings in one hand without telling me which, and 7 in the other, and give me choice of either of them; I say, it is the same thing as if he should give me 5 shillings.”
Huygens’ Criterion
Maximize the rate of change in the expectation value of wealth
. (6)
In modern terms, Huygens suggested to maximize the ergodic growth rate assuming additive dynamics.
Nicolas Bernoulli, in a letter to Montmort,20 challenged this notion by introducing a lottery whose expected prize, ⟨G(n)⟩, diverges positively with the number of possible outcomes, nmax. Since the expected rate of change in wealth 
is linear in ⟨G(n)⟩, it too diverges for any finite ticket fee F. According to Huygens’ Criterion, any finite ticket fee should be paid for the lottery. However, Bernoulli chose the lottery such that large prizes only occur with small probability, and found that typical individuals when (hypothetically) offered this lottery were not willing to pay much. This seeming incongruence became known as the St Petersburg paradox. From the modern perspective, the paradox challenges the notion of rationality defined as expectation-optimization, or the assumption of unrealistic additive dynamics. It exposes the following:
Huygens’ weakness
Expectation values are averages over ensembles of random realizations. The conceptual weakness of Huygens’s criterion is its limited relevance to an individual making a decision. The expectation value would be relevant over T rounds if the individual were part of a large resource-sharing group mimicking a statistical ensemble, where the group size N∝ exp(T).17,21 It would also be relevant if the wealth process x(t) were additive—the rate of change would then be ergodic and the expectation value would reflect how the individual fares over time. Wealth is often better modeled with multiplicative dynamics.
Specifically, Bernoulli proposed the following lottery: a fair coin is tossed until heads appears for the first time. The number of coin tosses, n∈{1,2…}, is modeled as a random variable with geometric distribution, p(n)=2−n. The prize as a function of n is G(n)=$2n−1. It follows that G(n) is power-law distributed with diverging first moment. The time δt to generate an instance of the random variable, i.e., to play the lottery, is considered independent of n in this study. The lottery is usually presented without restriction on n. For a more careful treatment of the problem, one must initially require n≤nmax. For more than nmax coin tosses, the lottery is declared invalid and no change in wealth occurs. The behavior of the original unrestricted case is investigated as the limit nmax→∞.
B. 1738–1814 decision theory: Utility
By 1738, N. Bernoulli’s cousin Daniel Bernoulli and Cramer [Ref. 5, p. 33] had conceptualized the problem as follows. They argued that people attach a value to money that is non-linear in the dollar amount. Cramer had written to Bernoulli in 1728: “in their theory [i.e., Huygens' Criterion] mathematicians evaluate money in proportion to its quantity while, in practice, people with common sense evaluate money in proportion to the utility they can obtain from it.” Bernoulli suggested a logarithm to map a dollar amount into utility, uB(x)=ln(x). We know today that this conceptualization is problematic. For instance, we must require that there be no distinguished currency (nothing physical depends on whether we quote wealth in dollars or cents). It follows that the numerical magnitude of a physically meaningful quantity can only change by some power of the exchange rate when we switch currencies. Since the logarithm is not a power law, this fundamental requirement from dimensional analysis is violated [Ref. 22, p. 17 ff].
The quantity, Bernoulli suggested, that people consider when deciding whether to take part in the lottery is a combination of the expected gain in their utility if no ticket fee were paid, and the loss in utility they suffer when they pay the ticket fee. This leads to the following criterion:
Bernoulli’s criterion
A lottery ticket is worth buying if the following quantity is positive [Ref. 5, pp. 26–27]:
(7)
The first terms on either side of the equation represent the expected gain in logarithmic utility, resulting from the prizes of the lottery. This would represent the net change in utility if tickets were given away for free, F=0. The second terms represent the loss in logarithmic utility suffered at the time of purchase, i.e., after the ticket is bought but before any prize is received. This is inconsistent with expected-utility theory.8 The conceptual inconsistency may be phrased as follows: Bernoulli thought of utility as a new currency, but currency conversion is always linear—at odds with the non-linear logarithm favored by Bernoulli.
Bernoulli’s inconsistency
Bernoulli’s Criterion is mathematically inconsistent with later work in expected-utility theory because Bernoulli did not calculate the expected net change in logarithmic utility. He did not only replace money with utility of money but also computed an observable other than the expected change in this new object.
C. 1814–1934 Decision theory: Expected utility
The consensus in the literature on utility theory is that Bernoulli meant to compute the expected net change in utility and made a slight error. Laplace4 re-told Bernoulli’s resolution of the St Petersburg paradox and the invention of utility. Perceiving Bernoulli’s Criterion as an error, he implicitly “corrected” Bernoulli’s formal inconsistency without mention.
Laplace’s criterion
Maximize the expected rate of change in logarithmic utility [Ref. 4, pp. 439–442]
(8)
Later researchers adopted Laplace’s corrected criterion. Todhunter23 followed Laplace, as do modern textbooks in stating that utility is an object encoding human preferences in its expectation value.16,24,25 Laplace stayed within Bernoulli’s conceptual framework and was almost certainly not aware of the physical interpretation of his criterion as the ergodic growth rate under multiplicative dynamics (Eq. (5)).
Bernoulli motivated the logarithm by suggesting that the perceived utility change induced by an extra dollar is inversely proportional to wealth, leading to the differential equation du(x)=x−1dx, whose solution is the logarithm. But Bernoulli also considered Cramer’s suggestion of uC=√x a good representation of diminishing marginal utility. The modern perspective takes Bernoulli’s logarithm more seriously than he himself did. The route to the modern treatment of the gamble problem is to ask: “What if the logarithm was not merely convenient and a good fit to the data, what would be its physical meaning if it truly was a logarithm?” Using the logarithm in exactly the same place as the utility function is equivalent to assuming multiplicative dynamics and constructing an ergodic observable.
D. Post-1934 decision theory: Bounded utility
Karl Menger6 re-visited Bernoulli’s 1738 study, and came to the incorrect conclusion that only bounded utility functions are permissible. Of course, whether a utility function, or anything else, is bounded or not in the limit of diverging wealth is practically irrelevant because wealth expressed in money will always be represented by a finite number, as was pointed out, e.g., by Coolidge.26 However, based on formal arguments, Menger drew conclusions for the structure of the permissible formalism, namely, he ruled out linear and logarithmic functions as models of behavior, and, equivalently, additive and multiplicative processes as models of wealth. Because of the central role of these dynamical models, the development of decision theory suffered from this restriction, and it is satisfying to see that formal arguments against these important models are invalid, as intuition would suggest. Menger must have been unaware of the correction to Bernoulli’s work by Laplace. His error may be phrased as using Bernoulli’s Criterion instead of Laplace’s, and only considering the first term in Bernoulli’s Criterion, implicitly setting the ticket fee to zero, F=0. The invalidity of Menger’s claim was pointed out by Peters.8,18 Menger’s argument survives as received wisdom. For completeness, we state it here and specify the invalid inferences involved.
Menger’s flawed argument
1. Logarithmic utility resolves the original St Petersburg paradox because it turns exponentially increasing money prizes, G(n)∝ exp(n), into linearly increasing utility-prizes δu(n)∝ n for large n.
2. If money prizes increase even faster, e.g., as the exponential of an exponential, exp(exp(n)), then expected utility changes will diverge positively as nmax diverges, just as expected wealth changes diverge for exponentially increasing prizes.
3. In such games, logarithmic utility predicts that the player will be willing to pay any ticket fee, just as linear utility does for exponentially increasing prizes. In this sense, logarithmic utility is not qualitatively different from linear utility. For utility theory to achieve the desired generality, utility functions must be bounded.