Полное решение должно описывать рост человечества в течение трех эпох. Первая эпоха А а нтропогенеза начинается с линейного роста с указанной выше минимальной скоростью. Когда население достигает величины порядка ста тысяч начинается эпоха В в зрывного роста со скоростью роста, пропорциональной квадрату населения Земли и в эту эпоху человек начал быстро заселять всю планету. Далее, когда скорость квадратичного роста достигла своего предела и стала порядка удвоения за характерное время , наступает кризис мирового демографического развития, переход в эпоху С с табилизации населения мира в рамках приближений развитой теории. В результате на основании (3) максимальная абсолютная скорость роста глобального во время демографического перехода равна

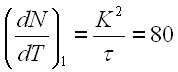млн. в год при относительном росте 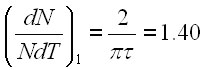% в год (7)

в 1995 году, что согласуется с данными ООН, но дает несколько меньшее значение для абсолютной скорости роста при сравнении с Таблицей 1. См. Рис. 6. Население нашей планеты в этот момент равно:

млн.

(8)

На основе этих представлений легко определить предел в два раза больший чем , к которому в эпоху С асимптотически стремится население Земли:

млн.

(9)

В рамках сделанных предположений это представляет верхнюю оценку населения Земли в предвидимом будущем. Таким образом, глобальное взаимодействие приводит к ускорению и синхронизации процессов и на заключительной стадии демографического перехода – к сужению перехода и тем самым к снижению предела для населения Земли.

Начальный линейный рост дает оценку времени для эпохи антропогенеза – критического момента в начале предистории человечества, которое произошло

млн. лет тому назад,

(10)

если использовать известные нам значения и . Несмотря на сделанные упрощения, данная оценка вполне согласуется с оценками этого времени в антропологии, также известного только приближенно.

Если проинтегрировать численность населения от до нашего времени :

млрд.

(11)

то получим оценку для числа людей, когда-либо живших. Множитель появился, поскольку в оценках других авторов длительность поколения принята равной 20 годам, которые ведут к оценке для млрд. [10]. Таким образом, в течение каждого из выделенных периодов жило по млрд. людей. Из (11) следует, что это число является инвариантным для числа людей живших в экспоненциально сокращающихся циклах и где указывает число циклов. Рассмотрение N (Т) как аналитической функции указывает на асимптотическое поведение при , когда , в предположении что в обозримом будущем нет особенностей роста – полюсов или нулей. Циклы можно получить, обобщая решение (6) в область комплексных переменных или же, просуммировав сокращающиеся циклы , определить длительность развития:

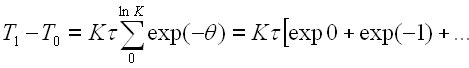	(12)

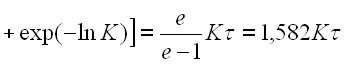и сравнить ее с (10), где эта длительность равна . В первом случае рост суммируется по гиперболической траектории, во втором по – . Демографические циклы определяют периодичность развития всего человечества за 4 – 5 миллиона лет, включая и проходящий по гиперболическому закону рост с момента конца антропогенеза до наших дней.

Для дальнейшего перейдем к переменной , когда мерой численности становится K . Тогда уравнения для роста приобретают симметричный вид и видно как сопряжены переменные и :

	(13 a )
	(13 b )
	(13 c )
	(13 d )

Сравнивая (13 a ) и (13 d ) видна смена переменных при прохождении перехода, когда становится независимой переменной вместо времени (см. (2)), и что затем выражено в уравнении роста (3).

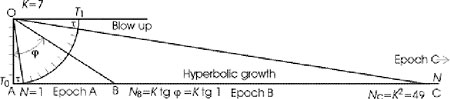
Рис. 8. Построение функции тангенса, показывающее пределы асимптотик роста при .

Рост населения можно иллюстрировать геометрическим построением функции тангенса:

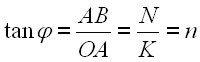(14)

связывающей угол и приращение населения . Линейный рост будет продолжаться до и в точке В на касательной АС. Дальнейший рост будет проходить по гиперболе, при которой время асимптотически стремиться к а население достигнет значение . Когда время приближается к моменту особенности, то от уравнения (13а) следует переходить к уравнению (13 d ), чтобы описать рост при прохождении особенности в течение эпохи С . Исходное построение показывает, что после перехода от линейного к гиперболическому росту на эпоху В остается в два раза меньше времени, чем на начальную эпоху А .

Построение, когда переменные и меняются местами при прохождении перехода мы оставляем читателю. Рис. 8 построен при , когда время от до разделено на 11 интервалов и, поскольку , то Однако даже при таком малом значения дает хорошую оценку для числа демографических циклов Так нулевой цикл антропогенеза продолжался 7 единиц времени, первый цикл длился 3 и последний – одну единицу времени. Это построение показывает как дискретность времени и населения приводит к появлению периодичности роста.

Для того чтобы выяснить устойчивость развития следует обратиться к уравнению роста человечества, выраженные в автономной форме, когда рост зависит от состояния системы, т. е. от n . В этом случае, преобразуя (4) получим общее уравнение роста:

(15)

где последний член добавлен с тем, чтобы рост никогда не был меньше одного гоминида при . Интегрируя (15) и при значениях К >> 1 получим решение при начальных условиях :

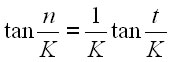(16)

Это решение показывает симметрию переменных N и T , населения и времени. Для развития в течение эпохи В вдали от особенностей роста это выражено в (13в), и следует из сложности причинных связей в рамках развитых представлений о нелинейной динамики глобальной системе населения нашей планеты.

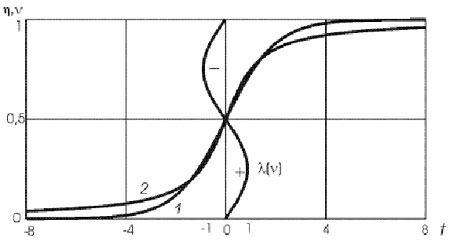
Рис. 9. Устойчивость роста в линейном приближении и переходные процессы

1 – логистический переход , 2 – демографический переход и

На основании (15) можно исследовать в линейном приближении устойчивость роста к возмущениям:

(17)

и определить показатель Ляпунова развития неустойчивости в системе населения Земли:

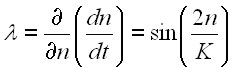(18)

дифференцируя (15). Следуя этому критерию при >0 движение неустойчиво. Следовательно, до перехода демографическая система неустойчива и только после развитие системы становится устойчивым и таким остается и впредь. В исторической хронологии мгновенный экспоненциальный масштаб времени роста линейной неустойчивости по Ляпунову зависит от древности и до демографического перехода равен удвоенному времени роста:

(19)

Однако мы видели, что выделенные антропологами и историками демографические циклы указывают на глобальную устойчивость роста с малыми отклонениями от предельной траектории роста. Исключением стало уменьшения населения мира на 8 – 10% в течение мировых войн ХХ в. См. Рис.10. Действительно, по критерию (16) максимальную неустойчивость можно ожидать вблизи начала мирового демографического перехода. Так в 1913 году экономики Германии и России росли на 10% в год, а население России на 2% в год, то в этих темпах можно видеть причину потери политической и экономической устойчивости Европы. Поэтому есть основания рассматривать мировые войны ХХ века как результат потери устойчивости демографической системы, как бы механистически это и не звучит.

Если же просуммировать недостачу населения мира за указанный период, то интегральные потери равны 11 000 млрд. человек лет. Приняв среднюю продолжительность жизни равной 40 годам, то определенные таким образом полные потери оказываются равными 280 ± 20 млн., что более чем в два раза больше принятых в демографии войн оценок ~ 120 млн. Демографические данные Таблицы 1 указывают, что после 1950 года население мира даже с небольшим перехлестом возвращается к своему расчетному значению, указывая на глобальную устойчивость развития.

Представляло бы интерес рассмотреть уравнения роста в области комплексного переменных при анализе устойчивости роста, а так же анализ флуктуаций при учете данных демографии и истории. На этом мы закончим краткое изложение теории роста и перейдем к обсуждению и применения её выводов.

4. Рост населения Земли

Гиперболический рост человечества, происходящий в режиме с обострением и превосходящий в десятки тысяч раз все сравнимые процессы, становится доминирующей функцией в решении дифференциального уравнения роста (3). Поэтому пространственное распределение населения и всё, связанное с конкретными локальными социальными и экономическими процессами, не может существенно повлиять на рост, где над всем превалирует глобальное взрывное развитие. В этом, исключительном по своей стремительности росте числа людей, следует искать причину того, почему простая асимптотическая модель режима с обострением оказы-вается такой эффективной и почему влиянием других переменных можно пренебречь.

В теории это разрешается путем обращения к феноменологическому подходу, когда с одной стороны мы описываем поведение системы в целом. С другой стороны, искать объяснение в детальных механизмах крайне затруднительно, да и не нужно, поскольку мы имеем дело с сильно связанной системой, где линейные причинно-следственные связи не работает. Тем не менее, в этой системе есть свои мощные регулирующие факторы, обеспечивающие устойчивый глобальный рост.

Эти соображения существенны тогда, когда возникает вопрос об управлении системой, особенно такой взаимосвязанной как демографическая система. Первое что необходимо – это более полное понимание динамики сложных систем. Быть может, здесь действительно могут быть полезны аналогии со сложными системами, изученные в физике. В этом можно видеть смысл вывода о том, что следует последовательно изучать демографическую историю всего человечества как динамической системы. Это ведет к пониманию статистической природы поведения сложной системы, где простых линейных причинно-следственные отношений нет. Наконец, необходимо учесть зависимость этих факторов от масштаба времени перемен. Так и стохастикой истории и стихией рынка можно и нужно управлять теми внешними связями, в которых, в частности, движется капитал. Но чем более длителен процесс развития, тем больше он должен быть детерминирован внешними факторами. Именно эта связь выражена в уравнении роста и служит подтверждением всей концепции теории, как теории эволюции сильно связанной системы. Только на этой основе можно понять, почему скорость роста связана со сложностью системы, а не с такими демографическими характеристиками, как рождаемость и смертность, когда возникает парадоксальная ситуация: в прошлом детей было много, а рост мал. В наше же время недостаток детей ограничивает рост и само воспроизводство населения в развитых странах, что будет подробно обсуждено ниже [5, 14]. См. Рис. 2.

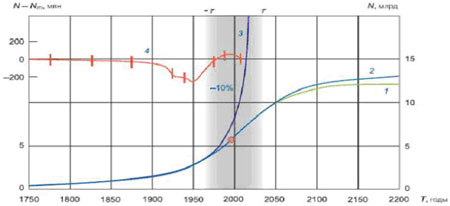
Рис. 10.   Рост  населения  мира  в  течение  демографической  революции 1750 – 2200гг.
1 – прогноз  IIASA, 2 – Модель, 3 – взрывной уход на бесконечность (режим с обострением), 4 – разница между расчетом и населением мира, увеличенная в 5 раз и где видны суммарные потери при Мировых войнах ХХ века, ? – 1995г. Продолжительность демографического перехода составляет 2 ? = 90 лет.

Глобальный рост определялся самосогласованным и самоподобным социальным системным развитием, обязанное коллективному взаимодействию, охватывающее всё человечество и за миллион лет эпохи В характер этого взаимодействия практически не изменился. В Таблице 1 приведена сводка последних данных и их разброс для населения Земли от возникновения человечества до предвидимого будущего [18]. На всем протяжении роста населения и в пределах той относительной точности данных оценки палеодемографии согласуются с результатами расчетов . Для оценок населения Земли в предвидимом будущем результаты моделирования можно сравнить с расчетами Международного института прикладного системного анализа (IIASA), ООН и других агентств. Прогноз ООН основан на ряде сценариев для рождаемости и смертности по 9 регионам мира и доведен до 2150г. По оптимальному сценарию население Земли к этому времени выйдет на постоянный предел 11 600 млн. По среднему варианту Популяционного отдела ООН к 2300г. ожидается 9 млрд. Таким образом, и прогнозы демографов и теория роста приводят к выводу, что население Земли стабилизируется на уровне 9 – 12 млрд. и даже не удвоится по сравнению с тем, что уже есть. Действительно, до рубежа 2000 г. население нашей планеты росло с постоянно  увеличивающейся скоростью. Тогда многим казалось, что демографический взрыв, перенаселение и неминуемое исчерпание ресурсов и резервов природы приведет человечество к катастрофе. Однако в 1995 г., когда население мира достигло 5,7 млрд., а темпы прироста населения – своего максимума 84 млн. в год или 220–240 тыс. человек в сутки, скорость роста начала уменьшаться, указывая на начало заключительной стадии глобального демографического перехода. В результате при грядущей стабилизации населения мира наступит новая эпоха истории. См. Рис. 2 и 4.

Таблица 1. Рост населения Земли (в миллнонах)

5. Сущность и преобразование собственного времени истории

В экспоненциальном сокращении длительности исторических периодов проявляется важнейшая для понимания динамики роста относительность времени в истории. Так Древний мир длился около трех тысяч лет, Средние века – тысячу лет, Новое время – триста лет, а Новейшая история – чуть более ста лет. См. Рис. 2. Историки давно обращали внимание на сокращение исторической длительности, однако чтобы понять уплотнение времени, его следует сопоставить с динамикой роста населения. В случае гиперболического роста время умножения пропорционально древности, исчисляемой от критической эпохи 2000 г. Так, 2000 лет тому назад население мира росло на 0,05% в год, 200 лет тому назад – на 0,5% в год, а 100 лет тому назад – уже на 1% в год. Максимальной скорости относительного роста 2% человечество достигло в 1960 году и это произошло на 35 лет раньше максимума абсолютного прироста населения мира.

Ускоренное развитие приводит к тому, что после каждого цикла на все оставшееся развитие приходится время, равное половине длительности прошедшего этапа. Так, после Нижнего палеолита, длившегося миллион лет, до нашего времени остается полмиллиона лет, а после тысячелетия Средних веков прошло 500 лет. Если история Древнего Египта и Китая занимала тысячелетия и исчисляется династиями, то поступь истории Европы определялась отдельными царствованиями [12]. Римская Империя, как это описано Гиббоном, распадалась в течение полутора тысяч лет, современные империи исчезали за десятилетия, а в случае Советской – и того быстрее. Благодаря замедлению времени в прошлом собственная длительность развития постоянна, но масштаб системного времени исторического развития изменяется, и процесс развития следует рассматривать в логарифмическом представлении времени.

Появление этого собственного времени развития человечества, времени которое справедливо было обозначено Франц Йозефом Радермахером как Eigen — Zeit , при неравновесном автомодельном росте приводит к сжатию времени исторического развития, когда скорость исторического процесса увеличивается по мере приближения к демографическому переходу. Для самого времени перехода рост населения Земли лучше всего передается на линейной сетке для Т и N . См. Рис.10.

Эта ситуация аналогична динамике в общей теории относительности, когда эволюция гравитирующей системы определяет само течение времени. Для самоорганизующихся систем представления о трансформации времени, его сцепления с процессом развития и связь с необратимостью роста рассмотрены Пригожиным [7]. Под влиянием идей Анри Бергсона французскими структуралистами было введено понятие длительности, связанное с самим процессом изменений в системе и отличное от хода часов мирового, ньютоновского, времени. Таким образом, появилось понятие пространства длительности longue dur e e , погружаясь в которое и следует рассматривать исторический процесс [11]. В случае взрывного развития человечества таким пространством является логарифмически преобразованное время. При этом системное, бергсоново время длительности равномерно и соответствует динамике роста, в отличие от внешнего, календарного – ньютоновского – времени.

В Таблице 2 показана вся история человечества, хронология которой структурирована на основании смены культур в циклы в соответствии с данными антропологии и истории. Антропологи и раньше обращались к логарифмической шкале времени, чтобы отобразить диапазон времен в Каменный век. Неолит, когда произошел переход от собирательства и охоты к сельскому хозяйству, происходит в логарифмическом времени точно посередине эпохи В десять тысяч лет тому назад.

Таблица 2. Рост  и  развитие  человечества  в  логарифмическом  представлении

Страницы: 1 2 3 4

© Сайт С.П. Курдюмова, 2003 - 2021 | Обратная связь

Эпоха	Период	Дата Годы	Число людей	Культурный цикл	D T лет	История, культура, технология
		2150	10 ? 10 9	Стабилизация		Переход к пределу 11 ? 10 9 Изменение возрастного
С		2050	9 ? 10 9	Населения Земли	125	распределения – старение Глобализация
	T 1	2000	6 ? 10 9	Мировой демографическ..	45	Урбанизация
	11	1955	3 ? 10 9	Переход	45	Компьютеры. Интернет Ядерная энергия
	10	1840	1 ? 10 9	Новейшая история	125	Мировые войны Электричество и радиосвязь
	9	1500		Новая история	340	Промышленная революция Книгопечать
	8	500 нэ		Средние века	1000	Географические открытия Падение Рима, Мухаммад
	7	2000 днэ	10 8	Древний мир	2500	Христос, ‘Осевое время’ Греческая цивилизация Индия, Китай, Будда и Конфуций
В	6	9000		Неолит	7000	Междуречье, Египет Письменность, города, бронза Одомашнивание скота, сел. / хоз.
	5	29 000	10 7	Мезолит	20 000	Керамика, Микролиты
	4	80 000		Мустье	51 000